Краткие теоретические сведения. 4.1.1. Постановка задачи:

4.1.1. Постановка задачи:

Требуется вычислить интеграл вида , где f(x) - подынтегральная функция, непрерывная на [a,b]; a, b - нижний и верхний пределы интегрирования.

Геометрически вычисление определенного интеграла интерпретируется как вычисление площади, ограниченной осью OX и графиком f(x) на промежутке [a,b] изменения х.

Аналитически эта задача решается в два этапа:

1) Вычисляется первообразная функции f(x), т.е. неопределенный интеграл ;

2) По формуле Ньютона-Лейбница вычисляется значение определенного интеграла:

На практике зачастую выполнить первый этап бывает затруднительно или в принципе невозможно, поэтому приходится использовать какие-либо численные методы.

Суть большинства методов численного интегрирования состоит в замене подынтегральной функции f(x) аппроксимирующей функцией , для которой можно легко записать первообразную в элементарных функциях, т.е.

,

где S - приближенное значение интеграла;

R - погрешность численного вычисления интеграла J.

При численном интегрировании независимо от выбранного метода необходимо вычислять приближенное значение S интеграла и оценивать погрешность R.

Наиболее популярными являются методы Ньютона-Котеса, в которых промежуток интегрирования [a,b] разбивается на некоторое число n интервалов, на каждом из которых подынтегральная функция f(x) заменяется на полином некоторой степени и вычисляется частичный интеграл, а конечный результат S есть сумма всех частичных интегралов. Методы Ньютона-Котеса отличаются друг от друга степенью используемого полинома. Например, методы прямоугольников (левых, правых, средних) используют полином нулевой степени, т.е. константу, метод трапеций – полином первой степени, т.е. наклонную прямую линию, метод Симпсона – полином второй степени и т.д.

4.1.2. Метод средних прямоугольников.

В этом методе подынтегральная функция f(x) на каждом интервале разбиения заменяется полиномом нулевой степени, т.е. константой, равной значению функции f(x) в середине интервала разбиения. Введем следующие обозначения: точку a на оси OX обозначим через x0, точку b - через xn, а точки разбиения промежутка [a,b] - через x1, x2,..., xn-1. Предполагается, что длина интервала разбиения постоянна на всем [a,b].

Обозначим ее через h: ; x_i= x_i-1 + h, i =1,2,...,n.

Тогда в методе средних прямоугольников площадь каждого i-го прямоугольника S_i определяется формулой , i = 0,1,2,...,n-1, а конечный результат:

.

Главный член погрешности метода средних прямоугольников, являющийся первым членом разложения ошибки R в ряд Тейлора, определяется формулой

.

4.1.3. Метод трапеций

В этом методе подынтегральная функция f(x) на каждом интервале разбиения [xi,xi+1] заменяется полиномом первой степени, т.е. наклонной прямой линией. Эта прямая проводится через значения f(x) на границах интервала. В этом случае приближенное значение частичного интеграла определяется площадью трапеции:

,

а численное значение интеграла на всем [a,b]

.

Главный член погрешности метода трапеций определяется формулой

.

4.1.4. Уточнение метода трапеций по Ричардсону

Если в формуле главного члена погрешности метода трапеций величину , независящую от шага разбиения h, обозначить через С, то сама формула принимает вид R₀=h²C.

Для уточнения метода трапеций можно применить следующую манипуляцию: вычисляются два значения S_h1 и S_h2 одного и того же интеграла для разных разбиений h₁ ≠ h₂. Тогда можно записать: и 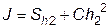. Если вычесть эти два уравнения друг из друга, то можно определить . Тогда, подставляя это выражение для С в одну из формул для J, получаем:

.

Вычисленное таким образом значение интеграла является гораздо лучшим приближением, чем S_h1 или S_h2.

Этот метод называется экстраполяционным переходом к пределу или уточнением по Ричардсону.

Задание

Изучить теоретический материал: численные методы вычисления определенного интеграла: методы левых, правых, средних прямоугольников, метод трапеций, уточнение по Ричардсону.

Требуется вычислить интеграл вида

,

где f(x) – подынтегральная функция, непрерывная на [a,b];

a, b – нижний и верхний пределы интегрирования.

Требуется вычислить значение интеграла S_C методом средних прямоугольников при числе N=20 разбиений промежутка [a,b], а также для двух разных разбиений N₁=10, N₂=20 значения S_T1,S_T2 методом трапеций, по которым определить уточнение S_R по Ричардсону. Для визуальной оценки точности вычислений требуется также вычислить точное значение интеграла J, для чего в качестве подынтегральных функций f(x) в приводимой ниже таблице вариантов выбраны такие, для которых известны первообразные функции F(x) в аналитическом виде (они также даны в таблице вариантов). Значение J вычисляется по формуле Ньютона-Лейбница: J=F(b)-F(a).

Для защиты контрольной работы представить на компьютере EXCEL-файл решения задачи и рукописный отчет. В отчете по задаче 4 представить:

1) значение интеграла S_C, вычисленное методом средних прямоугольников для N=20;

2) значения интеграла S_T1,S_T2, вычисленные методом трапеций для N₁=10 и N₂=20 соответственно;

3) уточнение по Ричардсону S_R;

4) точное значение определенного интеграла J;

5) ошибки R_C, R_T1, R_T2, R_R значений S_C, S_T1, S_T2, S_R по сравнению с J.

Пример решения задачи

В данном примере рассматривается вычисление интеграла

.

Первообразная подынтегральной функции:

A1’Вычисление определенного интеграла

Из таблицы вариантов выбрать интеграл, пометить его, скопировать и поместить как графический объект следом за введенным текстом.

A2’Промежуток интегрирования:

Объединяем клетки A2:C3, центрируем по вертикали и горизонтали.

D2’a E2’b . В клетки D3, E3 помещаем пределы интегрирования. В данном примере: D30,2 E21,4 .

Готовим таблицу для метода средних прямоугольников:

A4’Метод средних прямоугольников

Объединяем клетки A4:В4, центрируем по вертикали и горизонтали. Перенос текста на новую строку внутри клетки можно выполнить одновременным нажатием клавиш Alt и Enter.

A5’N= B5’20 A6’h= B6’ =($E$3-$D$3)/B5 . Здесь знак абсолютной адресации $ используется для копирования в дальнейшем формулы из клетки B6 в клетки E6 и G6.

A7’х В7’f(x)

A8=D3+B6/2 B8==1/(SIN(A8)*COS(A8)) – это формула для вычисления подынтегральной функции f(x).

A9= A8+$B$6 Копируем клетку В8 в В9

Копируем клетки А9:В9 в А10:В27 В результате получили таблицу значений f(x) в серединах интервалов разбиения промежутка интегрирования.

Готовим таблицу для метода трапеций:

D4’Метод трапеций Объединяем клетки D4:G4, центрируем по горизонтали.

D5’N1= E5’10 F5’N2= G5’20 D6’h1= F6’h2=

Копируем клетку В6 в клетку Е6 и в клетку G6

Копируем клетки А7, В7 в клетки D7,E7 и в клетки F7,G7

D8=D3 F8=D3 D9= D8+$E$6 F9= F8+$G$6

Копируем клетку В8 в клетки E8, E9, G8, G9

Копируем клетки D9:E9 в D10:E18 В результате получили таблицу значений f(x) в точках разбиения промежутка интегрирования на 10 частей.

Копируем клетки F9:G9 в F10:G28 В результате получили таблицу значений f(x) в точках разбиения промежутка интегрирования на 20 частей.

По результатам табулирования подынтегральной функции в ячейках F7:F28, G7:G28 строим график f(x).

Переходим к вычислению значений интеграла и ошибок методов:

A28’Первообразная Из таблицы вариантов выбрать запись F(x), пометить ее, скопировать и поместить как графический объект следом за введенным текстом.

A29’J= B29 =LN(ABS(TAN(E3)))-LN(ABS(TAN(D3)))

A30’Sc= B30 =B6*СУММ(B8:B27)

A31’ST1= B31 =E6/2*(E8+E18)+E6*СУММ(E9:E17)

A32’ST2= B32 =G6/2*(G8+G28)+G6*СУММ(G9:G27)

A33’Sr= B33 =(B31*G6^2-B32*E6^2)/(G6^2-E6^2)

Вычисляем значения ошибок методов:

С29’ошибка метода

С30’Rc= D30 =ABS($B$29-B30)

С31’RT1= Копируем D30 в D31, D32, D33

С32’RT2=

С33’Rr=

Для косвенной проверки полученных результатов вычислим отношения ошибок и . Если они будут приблизительно равны соответственно 0,5 и 4, то это означает, что вычисления произведены верно.

E30’Rc/RT2= F30 =D30/D32

E31’RT1/RT2= F31 =D31/D32

Полученная в результате описанных действий электронная таблица:

	A	B	C	D	E	F	G
	Вычисление определенного интеграла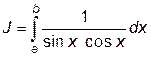
	Промежуток интегрирования:	a	b
	0,2	1,4
	Метод средних прямоугольников		Метод трапеций
	N=			N1=		N2=
	h=	0,06		h1=	0,12	h2=	0,06
	x	f(x)		x	f(x)	x	f(x)
	0,23	4,505031		0,2	5,135865	0,2	5,135865
	0,29	3,649476		0,32	3,348987	0,26	4,025116
	0,35	3,104541		0,44	2,594913	0,32	3,348987
	0,41	2,735432		0,56	2,221974	0,38	2,903089
	0,47	2,476602		0,68	2,045273	0,44	2,594913
	0,53	2,292643		0,8	2,000853	0,5	2,37679
	0,59	2,163083		0,92	2,074725	0,56	2,221974
	0,65	2,07564		1,04	2,290602	0,62	2,114648
	0,71	2,022957		1,16	2,731377	0,68	2,045273
	0,77	2,000949		1,28	3,64063	0,74	2,008272
	0,83	2,007984		1,4	5,97036	0,8	2,000853
	0,89	2,044579				0,86	2,02247
	0,95	2,113494				0,92	2,074725
	1,01	2,220265				0,98	2,161668
	1,07	2,374365				1,04	2,290602
	1,13	2,591504				1,1	2,473728
	1,19	2,898236				1,16	2,731377
	1,25	3,341843				1,22	3,098685
	1,31	4,013955				1,28	3,64063
	1,37	5,116597				1,34	4,490601
	Первообразная:		1,4	5,97036
	J=	3,353472	ошибка метода	проверка
	Sc=	3,344951	Rc=	0,008521	Rc/RT2=	0,496011
	ST1=	3,420294	RT1=	0,066822	RT1/RT2=	3,889710
	ST2=	3,370651	RT2=	0,017179
	Sr=	3,354103	Rr=	0,000632

 

Таблица индивидуальных заданий

№	Интеграл и его первообразная	[a, b]		№	Интеграл и его первообразная	[a, b]
		[0, 1.2]				[-0.5, 1.0]
		[-2, 2]				[0, 4.5]
		[0,3]				[0, 10]
		[-1, 1.4]				[0, 2]
		[-3, 3]				[0.5, 3]
		[0, 10]				[2, 5]
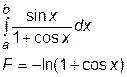
		[-1, 1.5]				[-1,5 1,5]
		[0, 4]				[1, 3]
		[2, 12]				[5, 10]
		[0.5, 2.5]				[0.5, 2.5]
		[0, 5]				[-2, 2]
		[1, 9]				[2.5, 5.5]
		[0.2, 1.5]				[1, 3]
		[-3, -1]				[0, 3]
		[-10, 0]				[1.2, 5.2]
		[1, 4]				[0.1, 3.1]
		[-5, 0]				[0, 3]

4.5. Контрольные вопросы

1. Как вычисляется определенный интеграл аналитически?

2. В чем состоит суть методов Ньютона-Котеса?

3. На что и как влияет количество разбиений при численном интегрировании? Можно ли увеличивая количество разбиений промежутка интегрирования бесконечно повышать точность интегрирования?

4. Как определяется значение частичного интеграла в методах прямоугольников?

5. В чем отличие методов левых, средних и правых прямоугольников?

6. Выберите правильный ответ на вопрос: «Чем отличаются методы прямоугольников, трапеций, Симпсона?»

а) числом разбиений промежутка интегрирования;

б) порядком аппроксимирующего полинома;

в) шагом интерполяции.

ЗАДАЧА 5. Решение задачи Коши для обыкновенных

дифференциальных уравнений