Указания к выполнению задания

1. Ознакомиться с таблицами для определения проекций карт мира, полушарий, карт материков и их крупных частей, карт океанов, а также карт бывшего СССР и РФ (табл. 2, 3, 4, 5, 6). Таблицы-определители организованы по единому принципу: в заголовках столбцов формулируются вопроcы (условия); последовательно отвечая на них и переходя от левых столбцов к правым, область поиска в пределах строк сужается; в крайнем правом столбце приведено полное название иcкомой проекции, для которой выполняются свое условия внутри соответствующей строки.

2. Ознакомиться с картографическими проекциями предлагаемых географических карт (приложение 1). Для определения проекции выяснить:

- какая территория изображена на карте и по какой таблице следует проводить определение;

- какова форма рамки географической карты;

- какими линиями (прямыми, кривыми, дугами концентрических или эксцентрических окружностей) изображаются меридианы ипараллели, у концентрических окружностей промежутки между смежными окружностями, измеренные циркулем-измерителем, равны по величине, у эксцентрических вследствие разных радиусов кривизны – изменяются.

- как изменяются промежутки между параллелями по прямому (среднему) меридиану;

- каковы дополнительные сведения о проекции.

3. По таблице-определителю дать полное название картографической проекции, выяснить класс проекции по виду вспомогательной геометрической поверхности, использованной при ее построении, и по характеру искажений.

Результаты работы должны быть представлены в виде таблицы (табл. 1), как показано в приведенном ниже примере выполнения задания.

Пример выполнения задания.

Определить картографическую проекцию (Рис. 1).

 

 

Рис. 1. Карта СССР

 

 

На карте изображена территория бывшего СССР, поэтому определение следует проводить по таблице 7. Форма рамки - прямоугольная. Меридианы изображены прямыми, что легко проверить, приложив к линии меридиана линейку. Параллели изображены дугами концентрических окружностей: любые три точки этой линии, перенесенные на кальку, всегда можно совместить, поворачивая кальку, с разными частями этой линии; промежутки же между двумя соседними параллелями остаются постоянными. Таким образом, по виду картографической сетки проекция является нормальной конической.

Расстояния между параллелями по среднему меридиану остаются постоянными. Следовательно, проекция равнопромежуточная по меридианам. Используя дополнительные признаки проекции - уточняем по определителю (табл. 7) название нормальная коническая равнопромежуточная проекция Каврайского. Результаты определения проекции записываются в таблицу 2. Для некоторых картографических проекций (в частности для карт мира и карт океанов) дополнительные указания могут отсутствовать.

 

Таблица 1

Варианты заданий

Номер варианта	Номер картогр.проекции (приложение 2)	Номер варианта	Номер картогр.проекции (приложение 1)
	2, 7, 26, 29		16, 20, 27, 36
	5, 14, 21, 25		8, 15, 29, 39
	3, 19, 24, 28		6, 19, 26, 28
	4, 17, 20, 36,		9, 22, 26, 39
	3, 10, 23, 35		2, 12, 15, 27
	16, 21, 26, 34		11, 17, 21, 30
	9, 14, 23, 33		2, 5, 9, 13
	18, 20, 28, 32		14, 16, 19, 38
	7, 24, 31, 34		4, 19, 23, 37
	11, 14, 23, 35		7,10, 18, 32
	2, 12, 26, 38		15, 20, 22, 28
	3, 13, 23, 33		5, 8, 25, 29

 

 

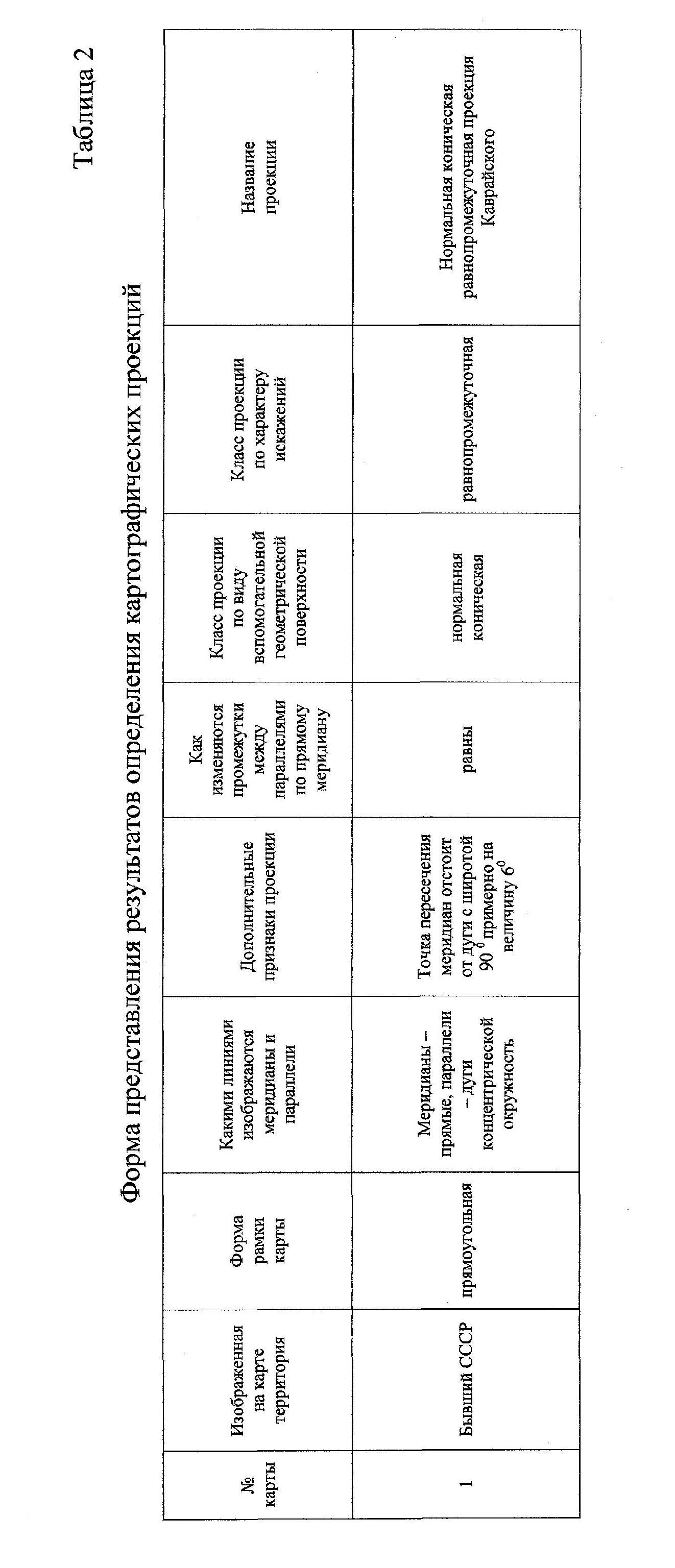
Таблица 3

Определитель проекций картографических сеток карт мира

Какова форма рамки карты или вид всей сетки	Какими линиями изображаются меридианы и параллели	Как изменяются промежутки между параллелями по прямому меридиану с удалением от экватора	Название проекции
Сетка и рамка прямоугольник, полюс в рамке не изображается	прямыми	Сильно увеличиваются: между параллелями 70 и 800 приблизительно в четыре с половиной раза больше, чем между экватором и параллелью 100	Нормальная цилиндрическая равноугольная проекция Меркатора
Увеличиваются: между параллелями 60 и 800 приблизительно 2,6 раза больше, чем между экватором и параллелью 200	Нормальная цилиндрическая проекция Урмаева 1945 года
Увеличиваются: между параллелями 60 и 800 приблизительно 1,8 раза больше, чем экватором и параллелью 200	Нормальная цилиндрическая проекция Урмаева 1948 года
Увеличиваются: между параллелями 70 и 800 приблизительно в 1,8 раза, чем между экватором и параллелью 100	Нормальная перспективно – цилиндрическая проекция Голла (БСАМ)
Рамка прямоугольник, полюс в рамке карты не изображается	Параллели – прямыми, меридианы - кривыми	Увеличиваются: между параллелями 70 и 800 почти в 1,5 раза больше, чем между экватором и параллелью 100	псевдоцилиндрическая проекция ЦНИИГАиК 1944года
Увеличиваются: между параллелями 60 и 800 почти 1,5 раза, чем между экватором и параллелью 200	Псевдоцилиндрическая проекция Урмаева
Параллели - дугами эксцентрических окружностей, меридианы - кривыми	Сохраняются равными	Поликоническая проекция ЦНИИГАиК 1950 года
Увеличиваются: между параллелями 70 и 800 приблизительно в 1,3 раза больше, чем между экватором и параллелью 100	Поликоническая проекция ЦНИИГАиК (для БСЭ)
Дугами окружностей	Увеличиваются: между параллелями 70 и 800 приблизительно в 2,3 раза больше, чем между экватором и параллелью 100	Круговая проекция Гринтена
Рамка прямоугольник, полюс изображается рядом прямых	Параллели –прямыми, меридианы - кривыми	Сохраняются равными	Псевдоцилиндрическая эллиптическая проекция Каврайского
Сильно уменьшаются: между параллелями 80 и 900 более чем в пять раз меньше, чем между экватором и параллелью 100	Псевдоцилиндрическая синусоидальная равновеликая проекция Каврайского
Сетка и рамка эллипс, полюс изображается точкой	Параллели – прямыми, меридианы - кривыми	Уменьшаются: между полюсом и параллелью 800 расстояние более чем в 2,5 раза меньше, чем между экватором и параллелью 100	Равновеликая псевдоцилиндрическая проекция Мольвейде
кривыми	Уменьшаются: приполярный промежуток составляет приблизительно в 2,5 раза меньше приэкваториального	Производная равновеликая проекция Аитова - Гаммера
Сетка с разрывами, полюс изображается несколькими точками	Параллели – прямыми, меридианы - кривыми	Уменьшаются: между полюсом и параллелью 800 расстояние примерно в 1,6 раза меньше, чем между экватором и параллелью 100	Равновеликая псевдоцилиндрическая синусоидальная проекция Мольвейде – Гуда с разрывами
Сетка с разрывами, полюс изображается рядом прямых	Сильно уменьшаются: между полюсом и параллелью 800 расстояние примерно в 3,5 раза меньше, чем между экватором и параллелью 100	Равновеликая псевдоцилиндрическая синусоидальная проекция БСАМ с разрывами

 

Таблица 4

Определитель проекций картографических сеток карт полушарий

Какими линиями изображаются параллели	Как изменяются промежутки по среднему (прямому) меридиану и экватору от центра полушария к его краям	Какой линией изображается экватор	Название проекции
окружностями или дугами окружностей	увеличиваются от 1 приблизительно до 2	прямой	поперечная азимутальная равноугольная (стереографическая) проекция
равны	окружностью	нормальная азимутальная равноугольная (стереографическая) проекция
окружностью	нормальная азимутальная равнопромежуточная проекция Посгеля
уменьшаются от 1 до 0,9	окружностью	нормальная азимутальная равновеликая проекция Ламберта
прямыми	сильно уменьшаются	прямой	поперечная азимутальная ортографическая проекция
удалением от среднего меридиана к крайним	уменьшаются от 1 приблизительно до 0,7	прямой	поперечная азимутальная равновеликая проекция Ламберта
уменьшаются от 1 приблизительно до 0,8		поперечная азимутальная проекция Гинзбурга
равны		поперечная азимутальная равнопромежуточная проекция Посгеля
увеличиваются от 1 приблизительно до 2		косая азимутальная равноугольная (cтepeoграфическая) проекция
уменьшаются от 1 приблизительно до 0.9		косая азимутальная равновеликая проекция Ламберта

 

Таблица 5

Определитель проекции картографических сеток карт и их материков

Как изменяются промежутки между параллелями по среднему (прямому) меридиану от центра материка к северу и югу	Какими линиями изображаются параллели и меридианы	Как изменяются промежутки между соседними параллелями с удалением от среднего меридиана к западу и к востоку	Какой линией изображается экватор	Название проекции
уменьшаются	Параллели и меридианы – кривыми, увеличивающими кривизну с удалением от среднего (прямого) меридиана к западу и востоку	увеличиваются	кривой	Косая азимутальная равновеликая проекция Ламберта
прямой	Поперечная азимутальная равновеликая проекция Ламберта
Параллели –концентрическими окружностей, меридианы - прямыми	уменьшаются	окружностью	Нормальная азимутальная проекция Ламберта
равны	Параллели –прямыми, меридианы - кривыми	Остаются постоянными	прямой	Равновеликая псевдоцилиндрическая синусоидальная проекция Сансона
Параллели – дугами концентрических окружностей, меридианы - кривыми	Дугой окружности	Равновеликая псевдоконическая проекция Бонна
Параллели – концентрическими окружностями, меридианы - прямыми	окружностью	Нормальная азимутальная равнопромежуточная проекция Постеля
Параллели- дугами концентрических окружностей, меридианы - прямыми	Дугой окружности	Нормальная коническая равноугольная проекция Каврайского 1934 года
увеличиваются	Параллели- концентрическими окружностями, меридианы - прямыми	Остаются постоянными	окружностью	Нормальная азимутальная равноугольная (стереографическая) проекция
кривыми	увеличиваются	кривой	Косая азимутальная равноугольная (стереографическая) проекция

 

 

Таблица 6

Определитель проекции картографических сеток карт океанов

Какова форма рамки	Какими линиями изображаются параллели и меридианы	Как изменяются промежутки между параллелями по среднему (прямому) меридиану с удалением от экватора	Название проекции
Рамка - окружность	Параллели- концентрическими окружностями, меридианы - прямыми	увеличиваются	Нормальная азимутальная равноугольная (стереографическая) проекция
равны	Нормальная азимутальная равнопромежуточная проекция Постеля
Сетка и рамка – прямоугольник, полюс в рамке карты не изображается	прямыми	Сильно увеличиваются: между параллелями 70 и 800 приблизительно в четыре с половиной раза больше, чем между экватором и параллелью 100	Нормальная цилиндрическая равноугольная проекция Меркатора
увеличиваются: между параллелями 60 и 800 приблизительно в 2,6 раза больше, чем между экватором и параллелью 200	Нормальная цилиндрическая проекция Урмаева 1945 года
увеличиваются: между параллелями 60 и 800 приблизительно в 1,8 раза больше, чем между экватором и параллелью 200	Нормальная цилиндрическая проекция Урмаева 1948 года
Рамка – прямоугольник, полюс в рамке карты не изображается	Параллели – прямыми, меридианы - кривыми	Незначительно уменьшаются	Псевдоцилиндрическая синусоидальная проекция Урмаева (с небольшими искажениями площадей)
Уменьшаются: между параллелями 70 и 800 в 2,1 раза меньше, чем между экватором и параллелью 100	Псевдоцилиндрическая синусоидальная проекция Урмаева
кривыми	Незначительно уменьшаются: между параллелями 60 и 700 в 1,1 раза меньше, чем между экватором и параллелью 100	Поперечная с овальными изоколами проекция ЦНИИГАиК
Рамка – прямоугольник, полюс изображается рядом прямых	Параллели – прямыми, меридианы - кривыми	Сохраняются равными	Псевдоцилиндрическая эллиптическая проекция Каврайского
Сильно уменьшаются: между параллелями 80 и 900 более чем в пять разменьше, чем между экватором и параллелью 100	Псевдоцилиндрическая синусоидальная равновеликая проекция Каврвйского

 

 

Таблица 7

Определитель проекций картографических сеток карт бывшего СССР и РФ

Какими линиями изображаются меридианы и параллели	Как изменяются промежутки между параллелями по среднему (прямому) меридиану	Дополнительные указания о проекциях	Название проекции
Параллели - дугами концентрических окружностей, меридианы - прямыми	Увеличиваются от средней величины к северу и к югу	Точка среднего полюса может быть получена в пересечении меридианов	Нормальная равноугольная коническая проекция Ламберта - Гауса
равны	Точка пересечения меридианов отстоит от дуги с широтой 900 примерно на величину 3 0	Нормальная коническая равнопромежуточная проекция Каврайского
Точка пересечения меридианов отстоит от дуги с широтой 900 примерно на величину 6 0	Нормальная коническая равнопромежуточная проекция Каврайского
Параллели и меридианы – кривыми	Увеличиваются к северу, между полюсом и параллелью 800 в 1,3 раза больше, чем между параллелью 40 и 500	Прямой меридиан – 1000 восточной долготы; сетка зрительно передает шарообразность Земли	Косая перспективно – цилиндрическая проекция Соловьева
равны	Прямой меридиан – 1200 восточной долготы; многие меридианы меняют направление выпуклости	Косая цилиндрическая равнопромежуточная проекция ЦНИИГАиК
Практически равны	Прямой меридиан – 900 восточной долготы	Косая азимутальная проекция ЦНИИГАиК
Незначительно уменьшаются от средней широты к северу и к югу	Прямой меридиан – 1000 восточной долготы; многие меридианы меняют направление выпуклости	Косая перспективно -цилиндрическая проекция ЦНИИГАиК
Параллели – дугами эксцентрических окружностей, меридианы - кривыми	Уменьшаются от юга к северу: между полюсом и параллелью 800 составляет 0,9 величины расстояния между параллелями 40 и 500	Прямой меридиан – 900 восточной долготы	Видоизмененная поликоническая проекция Салмановой

 

Задание 2. Вычисление нормальной равноугольной конической проекции (с двумя главными параллелями)

 

Цель задания. Вычислить и построить нормальную равноугольную коническую проекцию для карты в масштабе 1:25 000 000 (варианты задания в приложении 2).

Пример выполнения задания. Территория ограничена меридианами с долготой 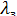=40° и =80° и параллелями с широтами = и 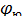= (рис. 6). Долгота среднего меридиана =60°. Картографическая сетка проведена через 10°, т. е. ∆ =∆ =10°

 

Рис 6. Сетка нормальной конической проекции Рис. 7. Сетка нормальной равноугольной конической проекции с двумя главными параллелями

Параметры проекции и 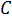найти с условием, что на двух главных параллелях с широтами =30° и =50° масштабы равны единице, т. е.

Параметры, используемые для вычисления:

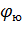- широта южной параллели территории;

- широта северной параллели территории;

- долгота западного меридиана территории;

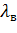- долгота восточного меридиана территории;

Δ 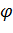-частота картографической сетки по широте;

Δ -частота картографической сетки по долготе;

Земная поверхность принимается за эллипсоид.

 

Формулы для вычисления проекции:

1. (1)

где r - радиусы параллелей земного эллипсоида;

2. (2)

где α и 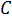- параметры проекции (постоянные величины);

– радиус главной параллели;

– масштаб ;

3. (3)

где – полярный угол;

4. (4)

где – радиус параллелей в проекции;

5. (5)

где – расстояние между полюсом полярной системы координат и началом счета прямоугольных координат на проекции (const = );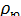

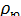– экваториальный радиус;

– радиус параллелей на проекции;

– прямоугольная координата;

(6)

где – прямоугольная координата;

6. 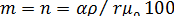(7)

где – масштаб по меридиану;

– масштаб по параллели;

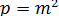(8)

где p– масштаб площади;

где 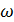– максимальное искажение углов в проекции;

Значение , , 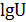выбирают в зависимости от широты параллелей из приложение 3.

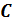Вычисления параметров и высчитывают по формулам (1) и (2), записываются в табл. 8 и табл. 9

Таблица 8

Вычисление параметров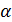

формула	Вычисленные значения для широт
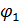
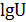
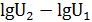
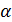
	6,7425955 6,6136233 0,2371064 0,4367044   0,1289722 0,1995980 0,6461597

 

Таблица 9

Вычисление параметров

Обозначение, формула	Вычисление значения для широт
φ1	φ1
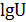
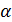
	0,2371064 0,4367044 0,6461597
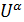
lgU	0,1532086   1,4230121 22,113396	0,2821807   1,9150525 16,431732
=	48,6995	48,6995

 

Вычисление полярного угла . Полярный угол высчитывают по формуле (3), данные приводят в табл. 10 по разностям долгот , где =70, 80, =60.

 

Таблица 10

Вычисление полярного угла δ

обозначение	Вычисление значения по разностям долгот
100	200
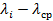
	0,6461597 100	200
	6,461612	12,9232

Вычисление радиуса параллелей. Радиус параллелей проекции высчитывают по формуле (4), данные приводят в табл. 11

 

Таблица 11

Радиусы параллелей проекции

Обозначение, формула	Вычисленные значения для широт
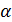
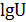
	0,6461597 0,1537787	0,2371064	0,3294572	0,4367044	0,5694259
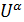
, см , см	0,0993655	0,1532086	0,2128819	0,2821807	0,3679400
1,257087	1,423012	1,632608	1,915052	2,333136
48,6995
38,7400	34,2228	29,8293	24,4299	20,8730
∆ , см	4,5172 4,3935 4,3994 4,5569

Вычисление прямоугольных координат и высчитывают по формулам (5) и (6), данные приводят в табл. 12; –const, близкое к значению радиуса южной параллели. В примере =40 см.

 

Таблица 12

Вычисление прямоугольных координат

	Обозначение, формула	Вычисленные значения для долгот
=60	50 и 70	40 и 80
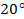
	cos sin	00 1.0	6.46160 0.99365 0.11254	12.92320 0.97465 0.22364
, см , см cos , см , см	1,260 40,000 38,740 38,740 0,0	1,506 40,000 38,494   4,360	2,241 40,000 37,759   8,664
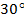
	, см , см cos , см , см	5,777 40,000 34,223 34,2228 0,0	5,995 40,000 34,005   3,851	6,644 40,000 33,356   7,654
	, см , см cos , см , см	10,171 40,000 29,829 29,8293 0,0	10,360 40,000 29,640   3,357	10,926 40,000 29,074   6,671
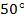
	, см , см cos , см , см	14,570 40,000 25,430 25,4299 0,0	14,732 40,000 25,268   2,862	15,214 40,000 24,786   5,687
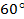
	, см , см cos , см , см	19,127 40,000 20,873 20,8730 0,0	19,260 40,000 20,740   2,349	19,656 40,000 20,344   4,668

 

Таблица 13

Значения абсцисс и ординат

	обозначение	Прямоугольные координаты (в см) для меридианов с долготами
λср = 600	500 и 700	400 и 800
		1,260 0.0	1,506 4,360	2,241 8,664
		5,777 0,0	5,995 3,851	6,644 7,654
		10,171 0,0	10,360 3,357	10,926 6,671
		14,570 0,0	14,732 2,862	15,214 5,687
		19,127 0,0	19,260 2,349	19,656 4,668

На основании табл. 13 на миллиметровой бумаге строят сетку нормальной равноугольной конической проекции с двумя главными параллелями. Начинают строить с правой стороны, затем в зеркальном отражении переносят координаты точек на левую сторону. Меридианы - прямые линии, параллели – дуги концентрической окружности (рис. 7).

Вычисление значения частных масштабов ( ) и масштаба площади р высчитывают по формулам (7) и (8), данные записывают в табл. 14.

 

Таблица 14

Вычисление частных масштабов и масштаба площади

Обозначение, формула	Вычисленные значения для широт φ
	0,64616 25,032 23,984 1,044 1,090	22,114 22,114 1,000 1,000	19,274 19,571 0,985 0,970	16,432 16,432 1,000 1,000	13,4857 12,788 1,055 1,113

На основании найденных масштабов длин и площадей строят график масштабов m и p (рис.8).

 

 

 

 

Рис. 8. График масштабов длин и площадей в нормальной равноугольной конической проекции

 

Задание 3. Вычисление нормальной равноугольной цилиндрической проекции

 

Цель задания. Вычислить и построить нормальную равноугольную цилиндрическую проекцию для карты в масштабе 1:25 000 000 (варианты задания в приложении 2).

Рис. 9. Сетка нормальной цилиндрической проекции Рис. 10. Сетка нормальной равноугольной