пгеолб рпзтеыопуфек йънетеойк у рпнпэша четпсфопуфопк фептйй йожптнбгйй

16.1 рПОСФЙЕ ЬОФТПРЙЙ ЙОЖПТНБГЙЙ Й ЬОФТПРЙКОПЗП ЪОБЮЕОЙС РПЗТЕЫОПУФЙ

йЪНЕТЕОЙЕ У ФПЮЛЙ ЪТЕОЙС ФЕПТЙЙ ЙОЖПТНБГЙЙ ТБУУНБФТЙЧБЕФУС ЛБЛ РТПГЕУУ, Ч ТЕЪХМШФБФЕ ЛПФПТПЗП ХНЕОШЫБЕФУС ОЕПРТЕДЕМЕООПУФШ Ч УЧЕДЕОЙСИ ПВ ЙЪНЕТСЕНПК ЧЕМЙЮЙОЕ.

нЕТХ ОЕПРТЕДЕМЕООПУФЙ ЧЩТБЦБАФ ЬОФТПРЙЕК, Б ЙОЖПТНБГЙС ЧЩТБ­ЦБЕФУС Ч ФЕИ ЦЕ ЕДЙОЙГБИ, ЮФП Й ЬОФТПРЙС.

рТЙ ЙЪНЕТЕОЙСИ ЧУМЕДУФЧЙЕ РПЗТЕЫОПУФЙ ЙЪНЕТЙФЕМШОПЗП РТЙВПТБ ЛПМЙЮЕУФЧП ЙОЖПТНБГЙЙ ОБ ЧЩИПДЕ РТЙВПТБ ЧУЕЗДБ НЕОШЫЕ ЛПМЙЮЕУФЧБ ЙОЖПТНБГЙЙ ОБ ЧИПДЕ. фБЛЙН ПВТБЪПН, Ч ТЕЪХМШФБФЕ ЙЪНЕТЕОЙС РПМХЮБ­ЕН ЛПМЙЮЕУФЧП ЙОЖПТНБГЙЙ

q = о (и) - о (∆)љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.1)

ЗДЕ о (и) - ЬОФТПРЙС ЧИПДОПЗП УЙЗОБМБ; о (∆) - ЬОФТПРЙС РПЗТЕЫОПУ­ФЙ. фБЛЙН ПВТБЪПН, ХЧЕМЙЮЕОЙЕ ЙОЖПТНБГЙЙ ПВ ЙЪНЕТСЕНПК ЧЕМЙЮЙОЕ ХНЕОШЫБЕФ ЬОФТПРЙА (ЙУИПДОХА ОЕПРТЕДЕМЕООПУФШ), ПДОБЛП РПМОПЗП ТБУЛТЩФЙС ОЕПРТЕДЕМЕООПУФЙ ДПУФЙЗОХФШ ОЕЧПЪНПЦОП ЙЪ-ЪБ ОБМЙЮЙС РПЗ­ТЕЫОПУФЕК ЙЪНЕТЕОЙС. ьОФТПРЙС УЙЗОБМБ У РМПФОПУФША ЧЕТПСФОПУФЙ т (И), УПЗМБУОП л.ыЕООПОХ, ПРТЕДЕМСЕФУС ФБЛЙН ЧЩТБЦЕОЙЕН

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.2)

у РПЪЙГЙК ФЕПТЙЙ ЙОЖПТНБГЙЙ РТПГЕУУ ЙЪНЕТЕОЙС РПОЙНБЕФУС ЛБЛ УПЛТБЭЕОЙЕ ДЙБРБЪПОБ ОЕПРТЕДЕМЕООПУФЙ ЙЪНЕТСЕНПК ЧЕМЙЮЙОЩ. фБЛ, ЕУМЙ РТЙВПТ ЙНЕЕФ РТЕДЕМЩ ЙЪНЕТЕОЙС ПФ X₁ ДП X₂, ФП ЧЕТПСФОПУФШ РПМХЮЕОЙС ПФУЮЕФБ Ч РТЕДЕМБИ ЫЛБМЩ РТЙВПТБ ТБЧОБ ЕДЙОЙГЕ, Б ЪБ РТЕДЕМБНЙ ЫЛБМЩ - ОХМА .

оБРТЙНЕТ, РТЙ ТБЧОПНЕТОПН ТБУРТЕДЕМЕОЙЙ ЙЪНЕТСЕНПК ЧЕМЙЮЙОЩ Ч РТЕДЕМБИ ПФ X₁ ДП X₂ ОБЮБМШОБС ОЕПРТЕДЕМЕООПУФШ ПВ ЙЪНЕТСЕНПК ЧЕ­МЙЮЙОЕ (ДП ЙЪНЕТЕОЙС) ИБТБЛФЕТЙЪХЕФУС НБМПК РМПФОПУФША ЧЕТПСФОПУФЙ (ТЙУ 16.1)

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.3)

рПУМЕ ЙЪНЕТЕОЙС ОЕПРТЕДЕМЕООПУФШ УПЛТБФЙМБУШ ДП ЙОФЕТЧБМБ ОЕПРТЕ­ДЕМЕООПУФЙ d = 2∆ Й РМПФОПУФШ ЧЕТПСФОПУФЙ ХЧЕМЙЮЙМБУШ ДП ЧЕМЙЮЙОЩ

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.4)

йОБЮЕ, ЬОФТПРЙС ЪОБЮЕОЙК ЙЪНЕТСЕНПК ЧЕМЙЮЙОЩ ДП ЙЪНЕТЕОЙС

о (И) = ln ( и₂ - и₁)љ ,љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.5)

Б ЬОФТПРЙС РПЗТЕЫОПУФЙ

о (∆) = ln d = ln 2∆ ,љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.6)

ФПЗДБ ЛПМЙЮЕУФЧП ЙОЖПТНБГЙЙ

рПУМЕДОЕЕ УППФОПЫЕОЙЕ

q = ln N, ЕУМЙ N = (и₂ - и₁) / d_Ь,

УРТБЧЕДМЙЧП РТЙ МАВПН ЪБЛПОЕ ТБУРТЕДЕМЕОЙС ЧЕТПСФОПУФЕК РПЗТЕЫОПУ­ФЙ, РПЬФПНХ ЮЙУМП N ВЩМП РТЕДМПЦЕОП ОБЪЩЧБФШ ЮЙУМПН ТБЪМЙЮОЩИ ЗТБ­ДБГЙК ЙЪНЕТСЕНПК ЧЕМЙЮЙОЩ (ЮЙУМПН ЬЛЧЙЧБМЕОФОЩИ ДЕМЕОЙК) Ч ДЙБРБ­ЪПОЕ X₂ - X₁ РТЙ ДБООПН ЪБЛПОЕ т(И) ТБУРТЕДЕМЕОЙС РПЗТЕЫОПУФЙ, Б d_Ь - ЬЛЧЙЧБМЕОФОЩН (Ч БОФТПРКОПН УНЩУМЕ) ЙОФЕТЧБМПН ОЕПРТЕДЕМЕООПУФЙ.

ъОБЮЕОЙЕ ЬЛЧЙЧБМЕОФОПЗП ЙОФЕТЧБМБ ОЕПРТЕДЕМЕООПУФЙ НПЦОП НБ­ФЕНБФЙЮЕУЛЙ ПРТЕДЕМЙФШ ДМС МАВПЗП ЪБЛПОБ ТБУРТЕДЕМЕОЙС ЛБЛ ЧЕМЙЮЙ­ОХ, УФПСЭХА РПД ЪОБЛПН МПЗБТЙЖНБ Ч ЧЩТБЦЕОЙЙ ДМС о (∆), ХУФТБОСС ФЕН УБНЩН ЧПЪНПЦОПУФШ ЛБЛПЗП - МЙВП РТПЙЪЧПМБ.

оБРТЙНЕТ, ДМС ОПТНБМШОП ТБУРТЕДЕМЕООПК РПЗТЕЫОПУФЙ, Ф.Е. РТЙ

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.8)

Й

^{љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ} (16.9)

РПМХЮБЕН

љљљљљљљљљљљљљљљљљљљљљљљ (16.10)

хЮЙФЩЧБС, ЮФП

= 1

Й РП ПРТЕДЕМЕОЙА ДЙУРЕТУЙЙ

=δ²

РПМХЮБЕН

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ љљљљљљљљљљљ (16.11)

фПЗДБ ЬЛЧЙЧБМЕОФОЩК ЙОФЕТЧБМ ОЕПРТЕДЕМЕООПУФЙ

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.12)

бОБМПЗЙЮОП НПЦОП РПМХЮЙФШ, ЮФП РТЙ ТБЧОПНЕТОПН ЪБЛПОЕ ТБУРТЕДЕМЕ­ОЙС РПЗТЕЫОПУФЙ

,љљљ љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.13)

Б ЮЙУМП ТБЪМЙЮЙНЩИ ЗТБДБГЙК ЙЪНЕТСЕНПК ЧЕМЙЮЙОЩ

_{љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ} (16.14)

тБЪДЕМЕОЙЕ ДЙБРБЪПОБ X₂ - X₁ ЙЪНЕТСЕНПК ЧЕМЙЮЙОЩ ОБ ПФДЕМШОЩЕ ТБЪМЙЮЙНЩЕ ЗТБДБГЙЙ ОБ ПУОПЧБОЙЙ ЖПТНБМШОЩИ РТЙМПЦЕОЙК ФЕПТЙЙ ЙО­ЖПТНБГЙЙ Ч ЧЙДЕ ЖХОЛГЙПОБМБ (16.14) ДМС ЬОФТПРЙЙ РТЕДУФБЧМЕОП ОБ ТЙУ (16.2). ъДЕУШ ДЙБРБЪПО X₂ - X₁ ТБЪВЙФ ОБ ЬЛЧЙЧБМЕОФОЩЕ ЙОФЕТЧБМЩ d_Ь, ЧЩЮЙУМЕООЩЕ ХЛБЪБООЩН ЧЩЫЕ РХФЕН, Й ПФОПУЙФЕМШОП ГЕОФТБ ЛБЦДП­ЗП ФБЛПЗП ЙОФЕТЧБМБ ЛБЛ ОБЮБМБ ЛППТДЙОБФ РПУФТПЕОБ ЛТЙЧБС УППФЧЕФУФЧХАЭЕЗП ЪБЛПОБ ТБУРТЕДЕМЕОЙС РПЗТЕЫОПУФЙ (ТБЧОПНЕТОПЗП, ФТЕХ­ЗПМШОПЗП Й ОПТНБМШОПЗП).

йЪ ТЙУХОЛБ ЧЙДОП, ЮФП УНЩУМ ЫЕООПОПЧУЛПЗП ПРТЕДЕМЕОЙС ЬОФТП­РЙЙ РПНЕИЙ УПУФПЙФ Ч ФПН, ЮФП ФПМШЛП РТЙ ТБЧОПНЕТОПН ТБУРТЕДЕМЕОЙЙ РПЗТЕЫОПУФЙ ЗТБОЙГЩ ЙОФЕТЧБМПЧ ОЕПРТЕДЕМЕООПУФЙ (МПЗБТЙЖН ЮЙУМБ ЛПФПТЩИ ЕУФШ ЛПМЙЮЕУФЧП ЙОЖПТНБГЙЙ q = lnN) УПЧРБДБЕФ У ЗТБОЙГБНЙ ТБУРТЕДЕМЕОЙС РПЗТЕЫОПУФЙ, Ф.Е. ПФДЕМШОЩЕ РПМПУЩ РПЗТЕЫОПУФЕК МЙЫШ УПРТЙЛБУБАФУС НЕЦДХ УПВПК.

рТЙ ФТЕХЗПМШОПН, Б ФЕН ВПМЕЕ, РТЙ ОПТНБМШОПН ТБУРТЕДЕМЕОЙЙ РПЗТЕЫОПУФЙ ЬЛЧЙЧБМЕОФОЩЕ ЙОФЕТЧБМЩ ХЦЕ ТБЪНБИБ ТБУРТЕДЕМЕОЙС РПЗ­ТЕЫОПУФЕК Й ПРТЕДЕМСАФУС МЙЫШ ФПК ЮБУФША ТБУРТЕДЕМЕОЙС, ЗДЕ УПУТЕ­ДПФПЮЕОБ ПУОПЧОБС НБУУБ ЬФЙИ РПЗТЕЫОПУФЕК, Б ЛТБС ТБУРТЕДЕМЕОЙК РЕТЕЛТЩЧБАФУС.

рТЙ РТБЛФЙЮЕУЛПН ЙУРПМШЪПЧБОЙЙ РТЙЧЕДЕООЩИ УППФОПЫЕОЙКљ ХДПВОЕЕљ ПРЕТЙТПЧБФШљ У РПМПЧЙОПК ЙОФЕТЧБМБ d_Ь,љ ЙНЕОХЕНПК ЬОФТПРЙКОЩН ЪОБЮЕОЙЕН РПЗТЕЫОПУФЙ ∆_Ь.

жПТНБМШОП ЬОФТПРЙКОПЕ ЪОБЮЕОЙЕ РПЗТЕЫОПУФЙ ПРТЕДЕМСЕФУС ЙЪ УППФОПЫЕОЙК

о(∆) = lnd_Ь = ln2∆_Ь

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.15)

d_Ь = 2∆_Ь = Е^H(∆);љ љљљљљљљљљљ ∆_Ь =1/2 Е^H(∆)

уППФОПЫЕОЙЕ НЕЦДХ ∆_Ь Й δ ЪБЧЙУСФ ПФ ЧЙДБ ЪБЛПОБ ТБУРТЕДЕМЕОЙС Й ПР­ТЕДЕМСЕФУС ЬОФТПРЙКОЩН ЛПЬЖЖЙГЙЕОФПН л = ∆_Ь/δ

фБЛ, ДМС ОПТНБМШОПЗП ЪБЛПОБ

_{љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ} (16.16)

уМЕДПЧБФЕМШОП, л = 2,07

дМС ФТЕХЗПМШОПЗП ЪБЛПОБ (уЙНРУПОБ)љљ л = 2,02

дМС ТБЧОПНЕТОПЗП ЪБЛПОБ

= 1.73δ;љљљљ л = 1.73љљљљ љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.17)

пДОЙН ЙЪ ДПУФПЙОУФЧ ЬОФТПРЙКОПЗП ЪОБЮЕОЙС РПЗТЕЫОПУФЙ СЧМСЕФ­УС ПЮЕОШ РТПУФБС УЧСЪШ НПЭОПУФЙ РПНЕИЙ δ² У ЧОПУЙНПК ЕА ДЕЪЙОЖПТ­НБГЙЕК о(∆) ЙМЙ У РПМХЮБЕНЩН РТЙ ЙЪНЕТЕОЙЙ ЛПМЙЮЕУФЧПН ЙОЖПТНБГЙЙ q, Б ЙНЕООП

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.18)

ЙУЛМАЮБС ДПРХУЛБЕНЩК ВЕЪ ЬФПЗП РТПЙЪЧПМ.љ дЕКУФЧЙФЕМШОП, ДП РТЙНЕОЕОЙС ФЕПТЙЙ ЙОЖПТНБГЙЙ ОЕ ВЩМП ЖПТНБМШОПЗП МПЗЙЮЕУЛПЗП ПВПУОПЧБО­ОПЗП УППФОПЫЕОЙС НЕЦДХ УТЕДОЕЛЧБДТБФЙЮЕУЛЙН δ Й РТБЛФЙЮЕУЛЙ ОПТНЙ­ТХЕНЩН ("РТЕДЕМШОЩН") ∆_m ЪОБЮЕОЙСНЙ РПЗТЕЫОПУФЙ. фБЛ, РТЙ ТБЧОП­НЕТОПН ЪБЛПОЕ ТБУРТЕДЕМЕОЙС ХЛБЪЩЧБАФ ∆_m = 1.73δ, Б РТЙ ОПТНБМШОПН ЪБЛПОЕ ∆_m = 2δ РТЙ т_q = 0.955 МЙВП ∆_m = 3δ РТЙ т_q = 0.997.

лБЛ ЧЙДОП ЙЪ ЙЪМПЦЕООПЗП ЧЩЫЕ, ЬОФТПРЙКОПЕ ЪОБЮЕОЙЕ РПЗТЕЫ­ОПУФЙ РПЮФЙ ФПЮОП УППФЧЕФУФЧХЕФ РТБЛФЙЮЕУЛЙ ЙУРПМШЪХЕНЩН УЕКЮБУ ПГЕОЛБН УМХЮБКОЩИ РПЗТЕЫОПУФЕК. йОБЮЕ ЗПЧПТС, ЙУРПМШЪХЕНБС Ч ОБУ­ФПСЭЕЕ ЧТЕНС ПГЕОЛБ Ч ЧЙДЕ ∆_m ЙЪ УЕТЙЙ 20-30 ОБВМАДЕОЙК ПЮЕОШ

ВМЙЪЛБ Л ЙНЕООП ЬОФТПРЙКОПНХ ЪОБЮЕОЙА РПЗТЕЫОПУФЙ.

16.2 еДЙОЙГЩ ЙЪНЕТЕОЙС ЬОФТПРЙЙ Й ЛПМЙЮЕУФЧБ ЙОЖПТНБГЙЙ

еДЙОЙГБ ЙЪНЕТЕОЙС ЬОФТПРЙЙ Й ЙОЖПТНБГЙЙ ЪБЧЙУЙФ ПФ ЧЩВПТБ ПУ­ОПЧБОЙС МПЗБТЙЖНБ. рТЙ ФЕПТЕФЙЮЕУЛПН БОБМЙЪЕ ХДПВОП ЙУРПМШЪПЧБФШ ОБФХТБМШОЩЕ МПЗБТЙЖНЩ Й ФПЗДБ ЬОФТПРЙС Й ЙОЖПТНБГЙС ЙЪНЕТСАФУС Ч ФБЛ ОБЪЩЧБЕНЩИ ОБФХТБМШОЩИ ЕДЙОЙГБИ (УПЛТБЭЕООП - ОЙФ).

рТЙ БОБМЙЪЕ ХУФТПКУФЧ, ТБВПФБАЭЙИ Ч ДЧПЙЮОПН ЛПДЕ (ОБРТЙНЕТ ьгчн), ЙУРПМШЪХАФ ДЧПЙЮОЩЕ МПЗБТЙЖНЩ Й ФПЗДБ ЙОЖПТНБГЙА РПМХЮБАФ Ч ДЧПЙЮОЩИ ЕДЙОЙГБИ (УПЛТБЭЕООП - ВЙФ). й ОБЛПОЕГ, РТЙ БОБМЙЪЕ ХУФ­ТПКУФЧ, ТБВПФБАЭЙИ Ч ДЕУСФЙЮОПН ЛПДЕ, РПМХЮБАФ ДЕУСФЙЮОЩЕ ЕДЙОЙГЩ ЬОФТПРЙЙ (УПЛТБЭЕООП - ДЙФ).

уППФОПЫЕОЙЕ НЕЦДХ ЬФЙНЙ ЕДЙОЙГБНЙ УМЕДХАЭЕЕ:љ

1ДЙФ = 2,3 ОЙФ = 3,6 ВЙФ; 1 ОЙФ = 1,45 ВЙФ = 0,43 ДЙФ; 1 ВЙФ = 0,69 ОЙФ = 0,3ДЙФ.

уМЕДХЕФ РПНОЙФШ, ЮФП Ч ЧЩЮЙУМЕОЙСИ ЪОБЮЕОЙС X Й ∆љ ДПМЦОЩ РПДУФБЧМСФШУС Ч ПДОЙИ Й ФЕИ ЦЕ ЕДЙОЙГБИ.

16.3 чЩЮЙУМЕОЙЕ ЬОФТПРЙКОПЗП ЪОБЮЕОЙС РПЗТЕЫОПУФЙ РП ЬЛУРЕТЙНЕОФБМШОЩН ДБООЩН

ч УППФЧЕФУФЧЙЙ У ПРТЕДЕМЕОЙЕН

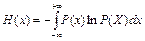
ъДЕУШ т (И) ПРТЕДЕМСЕФУС ЙЪ ЗЙУФПЗТБННЩ, ЗДЕ ДМС ЛБЦДПЗП УФПМВГБ т_i(И_i) = n_i/nd. рТЙ ЛПМЙЮЕУФЧЕ УФПМВГПЧ m Й ЛППТДЙОБФБИ ГЕОФТПЧ ЬФЙИ УФПМВГПЧ И_i РПМХЮБЕН

љљљљљ (16.19)

рТЕДУФБЧЙЧ РПУМЕДОЕЕ ЧЩТБЦЕОЙЕ Ч ЧЙДЕ

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.20)

РПМХЮБЕН ЧЩТБЦЕОЙЕ ДМС ПГЕОЛЙ ЬОФТПРЙКОПЗП ЪОБЮЕОЙС РПЗТЕЫОПУФЙ

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.21)

ьФБ ПГЕОЛБ СЧМСЕФУС УНЕЭЕООПК. дМС ЧЧЕДЕОЙС РПРТБЧЛЙ ОБ УНЕЭЕОЙЕ ПФ ОЕДПУФБФПЮОП ВПМШЫПЗП ЮЙУМБ n_i ОБВМАДЕОЙК РПМХЮЕООБС ПГЕОЛБ ДПМЦОБ ВЩФШ ХНОПЦЕОБ ОБ ЛПЬЖЖЙГЙЕОФ

љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (16.22)

 

 

м Й Ф Е Т Б Ф Х Т Б

1. пТОБФУЛЙК р.р. фЕПТЕФЙЮЕУЛЙЕ ПУОПЧЩ ЙОЖПТНБГЙПООП - ЙЪНЕТЙ­ФЕМШОПК ФЕИОЙЛЙ. - л.: чЩЭБ ЫЛПМБ, 1976.- 432 У.

2. тБВЙОПЧЙЮљ у.з.љ рПЗТЕЫОПУФЙљ ЙЪНЕТЕОЙК. м.:љ ьОЕТЗЙС, 1978.- 262 У.

3. ьМЕЛФТЙЮЕУЛЙЕ ЙЪНЕТЕОЙС ОЕЬМЕЛФТЙЮЕУЛЙИ ЧЕМЙЮЙО / РПД ТЕДБЛГЙЕК р.ч.оПЧЙГЛПЗП.- 5-Е ЙЪДБОЙЕ. - м.: ьОЕТЗЙС, 1975.- 576 У.

4. оПЧЙГЛЙК р.ч. пУОПЧЩ ЙОЖПТНБГЙПООПК ФЕПТЙЙ ЙЪНЕТЙФЕМШОЩИ ХУФТПКУФЧ.- м.: ьОЕТЗЙС, 1968.- 248 У.

5. оПЧЙГЛЙК р.ч., ъПЗТБЖ й.б. пГЕОЛБ РПЗТЕЫОПУФЙ ТЕЪХМШФБ­ФПЧ ЙЪНЕТЕОЙК.- м.: ьОЕТЗПЙЪДБФ, 1985.- 248 У.

6. лБТБУЕЧ б.й. фЕПТЙС ЧЕТПСФОПУФЕК Й НБФЕНБФЙЮЕУЛБС УФБ­ФЙУФЙЛБ.- н.: уФБФЙУФЙЛБ, 1970.- 344У.