 |
Главная |
Элементы квантовой механики
|
из
5.00
|
· Длина волны де Бройля
 ,
,
где  – постоянная Планка,
– постоянная Планка, 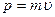 – импульс частицы.
– импульс частицы.
· Связь импульса релятивистской частицы с кинетической энергией
 ,
,
где m – масса частицы, 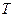 - кинетическая энергия.
- кинетическая энергия.
· При малых скоростях  .
.
· Соотношение неопределенностей Гейзенберга

 ,
,
где 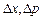 ,
,  - соответственно неопределенности координаты, импульса, энергии и времени,
- соответственно неопределенности координаты, импульса, энергии и времени, 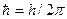 .
.
· Уравнение Шредингера:
 - нестационарное (общее);
- нестационарное (общее);
 - стационарное;
- стационарное;
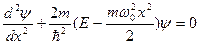 - стационарное для линейного гармонического осциллятора,
- стационарное для линейного гармонического осциллятора,
 - стационарное для кулоновского поля;
- стационарное для кулоновского поля;
 - стационарное для электрона в атоме водорода;
- стационарное для электрона в атоме водорода;
 - стационарное для свободной частицы в трёхмерном пространстве;
- стационарное для свободной частицы в трёхмерном пространстве;
 - стационарное для свободной частицы в одномерной потенциальной яме ,
- стационарное для свободной частицы в одномерной потенциальной яме ,
где  – волновая функция микрочастицы,
– волновая функция микрочастицы, 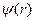 - координатная составляющая волновой функции,
- координатная составляющая волновой функции,  - полная энергия микрочастицы,
- полная энергия микрочастицы,  - потенциальная энергия частицы,
- потенциальная энергия частицы,  - пространственная координата, t – время,
- пространственная координата, t – время,
 - оператор Лапласа (записан в декартовых координатах),
- оператор Лапласа (записан в декартовых координатах),  – масса микрочастицы,
– масса микрочастицы,  – постоянная Планка,
– постоянная Планка,  =
=  - мнимая единица.
- мнимая единица.
· Условие нормировки волновой функции
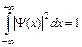
 .
.
· Плотности вероятности

 ,
,
где  – вероятность того, что частица может быть обнаружена вблизи точки с координатой
– вероятность того, что частица может быть обнаружена вблизи точки с координатой 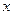 на участке
на участке  ,
,  - вероятность обнаружения микрочастицы в объёме
- вероятность обнаружения микрочастицы в объёме  .
.
· Вероятность обнаружения частицы в интервале от х1 до х2
 .
.
· Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика шириной
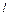 (0 ≥ x ≥
(0 ≥ x ≥ 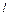 )
)
 (собственная нормированная волновая функция)
(собственная нормированная волновая функция)
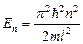 (собственное значение энергии),
(собственное значение энергии),
где 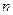 – главное квантовое число (
– главное квантовое число ( 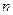 = 1, 2, 3,…). В области 0 ≥ x ≥
= 1, 2, 3,…). В области 0 ≥ x ≥ 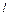
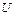 = ∞ и
= ∞ и  = 0.
= 0.
· Коэффициент прозрачности (коэффициент прохождения) прямоугольного потенциального барьера
 ,
,
где  - постоянный коэффициент, близкий к единице,
- постоянный коэффициент, близкий к единице,  - масса частицы,
- масса частицы,  - высота потенциального барьера,
- высота потенциального барьера, 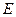 - энергия частицы,
- энергия частицы,  - ширина барьера.
- ширина барьера.
· Энергия квантового осциллятора
 ,
,
где 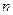 – главное квантовое число (
– главное квантовое число ( 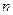 = 0, 1, 2,…),
= 0, 1, 2,…),  - циклическая частота.
- циклическая частота.
· Для частиц с целочисленными спинами (бозонов) справедлива статистика Бозе-Эйнштейна, а для частиц с полуцелыми спинами (фермионов) справедлива статистика Ферми-Дирака. Обобщенное уравнение для квантовых статистик
 ,
,
где  - среднее число частиц в состоянии с номером
- среднее число частиц в состоянии с номером 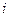 ,
,  - энергия частицы в этом состоянии;
- энергия частицы в этом состоянии;  – так называемый химический потенциал, определяемый из условия
– так называемый химический потенциал, определяемый из условия  , т. е. сумма всех частиц равна полному числу
, т. е. сумма всех частиц равна полному числу  частиц в системе, знак минус (-) перед единицей в знаменателе соответствует статистике бозонов (распределению Бозе-Эйнштейна, а знак плюс (+) соответствует статистике фермионов (распределению Ферми - Дирака).
частиц в системе, знак минус (-) перед единицей в знаменателе соответствует статистике бозонов (распределению Бозе-Эйнштейна, а знак плюс (+) соответствует статистике фермионов (распределению Ферми - Дирака).
|
из
5.00
|
Обсуждение в статье: Элементы квантовой механики |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

