Применение дифференциала в приближенных вычислениях

Понятие дифференциала

Пусть функция y = f(x) дифференцируема при некотором значении переменной x . Следовательно, в точке xсуществует конечная производная

Тогда по определению предела функции разность

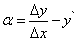(1)

является бесконечно малой величиной при . Выразив из равенства (1) приращение функции, получим

(2)

(величина 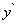не зависит от , т. е. остаётся постоянной при ).

Если , то в правой части равенства (2) первое слагаемое линейно относительно . Поэтому при

оно является бесконечно малой того же порядка малости, что и . Второе слагаемое - бесконечно малая более высокого порядка малости, чем первое, так как их отношение стремится к нулю при

Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

(3)

Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают

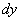
или

Следовательно,

(4)

или

(5)

Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента,

- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (5) это видно из записи, в формуле (4) – нет.

Дифференциал функции можно записать в другой форме:

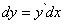(6)

или

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении xна величину .

Свойства дифференциала. Инвариантность формы дифференциала

В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.

Дифференциал обладает свойствами, аналогичными свойствам производной:

(С – постоянная величина) (8)

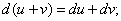(9)

(10)

(11)

(12)

Формулы (8) – (12) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .

Рассмотрим дифференциал сложной функции. Пусть - сложная функция :

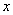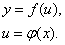
Дифференциал

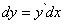
этой функции, используя формулу для производной сложной функции, можно записать в виде

Но есть дифференциал функции 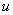, поэтому

,

т.е.

(13)

Здесь дифференциал записан в том же виде, как и в формуле (7), хотя аргумент 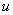является не независимой переменной, а функцией 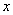. Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называютинвариантностью (неизменностью) формы дифференциала.

Подчеркнём, что в формуле (13) нельзя заменить на , так как

для любой функции 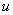, кроме линейной.

Пример 2. Записать дифференциал функции

двумя способами, выражая его: через дифференциал промежуточной переменной и через дифференциал переменной x . Проверить совпадение полученных выражений.

Решение. Положим

Тогда

а дифференциал запишется в виде

Подставляя в это равенство

и

Получаем

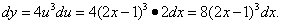
Применение дифференциала в приближенных вычислениях

Установленное в первом параграфе приближенное равенство

 

или

(14)

позволяет использовать дифференциал для приближенных вычислений значений функции.

Запишем приближенное равенство более подробно. Так как

а

то

или

(15)

Пример 3. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.

Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (15) в данном случае примет вид

Положим

тогда

Следовательно,

что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.

Пример 4.Пользуясь понятием дифференциала, вычислить приближенно

Решение. Число
является одним из значений функции

Так как производная этой функции

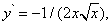
то формула (15) примет вид

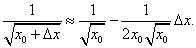
Полагая

и

получаем

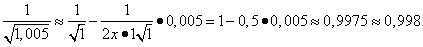
(табличное значение

).

Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.

Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:

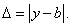(16)

Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:

(17)

Если точное число неизвестно, то

(18)

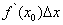Иногда, прежде чем применить формулу (15), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина была достаточно малой по сравнению с , так как чем меньше , тем, вообще говоря, точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина вычислялась просто.

Пример 5.Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.

Решение. Рассмотрим функцию

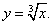
Её производная равна

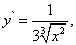
а формула (15) примет вид

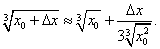
В данном случае было бы нерационально вычислять приближенно следующим образом:

так как значение

не является малым по сравнению со значением производной в точке

Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда

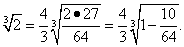
Теперь, полагая

получим

Умножая на 4/3, находим

Принимая табличное значение корня

за точное число, оценим по формулам (16) и (17) абсолютную и относительную погрешности приближенного значения: