 |
Главная |
Как найти направляющий вектор по общему уравнению прямой?
|
из
5.00
|
Если прямая задана общим уравнением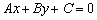 в прямоугольной системе координат, то вектор
в прямоугольной системе координат, то вектор  является направляющим вектором данной прямой.
является направляющим вектором данной прямой.
Пример 3.
Примеры нахождения направляющих векторов прямых:
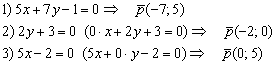
Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя в ряде случаев координаты направляющих векторов целесообразно сократить:
Так, уравнение  задаёт прямую, которая параллельна оси
задаёт прямую, которая параллельна оси  и координаты полученного направляющего вектора
и координаты полученного направляющего вектора  удобно разделить на –2, получая в точности базисный вектор
удобно разделить на –2, получая в точности базисный вектор  в качестве направляющего вектора. Логично.
в качестве направляющего вектора. Логично.
Пример 4
Составить уравнение прямой по точке  и направляющему вектору
и направляющему вектору  .
.
Решение: Формула 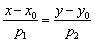 не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде
не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде  , и дальнейшее покатилось по глубокой колее:
, и дальнейшее покатилось по глубокой колее:

Ответ: 
Далее, перейдем к новому виду уравнения прямой – по двум точкам.
Уравнение прямой по двум точкам.
Если известны две точки  , то уравнение прямой, проходящей через данные точки, можно составить по формуле:
, то уравнение прямой, проходящей через данные точки, можно составить по формуле:

(координаты направляющего вектора: 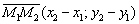
Примечание: точки можно «поменять ролями» и использовать формулу 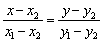
Пример 4. Составить уравнение прямой по двум точкам  .
.
Решение: Используем формулу:

Считаем знаменатели:

И методом пропорции решаем : 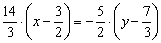
Именно сейчас удобно избавиться от дробных чисел. В данном случае нужно умножить обе части на 6:

Раскрываем скобки и доводим уравнение до ума:

Ответ: 
Далее переходим к виду прямой 5 – по точке и вектору нормали.
Нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), причём все векторы нормали прямой будут коллинеарными (сонаправленными или нет – без разницы).
Если прямая задана общим уравнением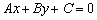 в прямоугольной системе координат, то вектор
в прямоугольной системе координат, то вектор  является вектором нормали данной прямой.
является вектором нормали данной прямой.
Если координаты направляющего вектора  приходиться аккуратно «вытаскивать» из уравнения, то координаты вектора нормали
приходиться аккуратно «вытаскивать» из уравнения, то координаты вектора нормали  достаточно просто «снять».
достаточно просто «снять».
Рассмотрим примеры с теми же уравнениями, что и для направляющего вектора:
Пример 5.

5.Уравнение прямой по точке и вектору нормали. Если известна некоторая точка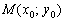 , принадлежащая прямой, и вектор нормали
, принадлежащая прямой, и вектор нормали  этой прямой, то уравнение данной прямой выражается формулой:
этой прямой, то уравнение данной прямой выражается формулой:
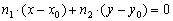
Пример 6.
Составить уравнение прямой по точке  и вектору нормали
и вектору нормали  . Найти направляющий вектор прямой.
. Найти направляющий вектор прямой.
Решение: Используем формулу:

Общее уравнение прямой получено:
Ответ: 
На чертеже ситуация выглядит следующим образом:

Далее рассмотрим уравнение прямой в отрезках:
1. Уравнение прямой в отрезках имеет вид  , где
, где  – ненулевые константы.
– ненулевые константы.
Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность 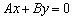 (так как свободный член
(так как свободный член  равен нулю и единицу в правой части никак не получить).
равен нулю и единицу в правой части никак не получить).
Пример 7
Дана прямая 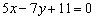 . Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.
. Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.
Решение: Приведём уравнение к виду  . Сначала перенесём свободный член в правую часть:
. Сначала перенесём свободный член в правую часть:

Чтобы получить справа единицу, разделим каждый член уравнения на –11:


Таким образом, точки пересечения прямой с координатными осями:

Ответ: 

Легко усмотреть, что данная прямая однозначно определяется красным и зелёным отрезками, отсюда и название – «уравнение прямой в отрезках».
И, наконец, последний нами рассматриваемый тип уравнения прямой:
7.Уравнение прямой в параметрической форме:
Если известна некоторая точка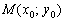 , принадлежащая прямой, и направляющий вектор
, принадлежащая прямой, и направляющий вектор 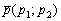 этой прямой, то параметрические уравнения данной прямой задаются системой:
этой прямой, то параметрические уравнения данной прямой задаются системой:

Пример 8
Составить параметрические уравнения прямой по точке  и направляющему вектору
и направляющему вектору 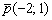
Решение:

|
из
5.00
|
Обсуждение в статье: Как найти направляющий вектор по общему уравнению прямой? |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

