 |
Главная |
Числовые характеристики статистического ряда
|
из
5.00
|
Основные понятия математической статистики
В медико-биологических задачах часто приходится исследовать распределение того или иного признака для очень большого числа индивидуумов. У разных индивидуумов этот признак имеет различное значение, поэтому он является случайной величиной. Например, любой лечебный препарата имеет различную эффективность при его применении к различным пациентам. Однако для того, чтобы составить представление об эффективности данного препарата, нет необходимости применять его ко всем больным. Можно проследить результаты применения препарата к сравнительно небольшой группе больных и на основании полученных данных выявить существенные черты (эффективность, противопоказания) процесса лечения. В связи с этим вводятся два понятия – генеральная совокупность и выборка.
Генеральная совокупность – подлежащая изучению совокупность однородных элементов, характеризуемых некоторым признаком.
Этот признак может быть как непрерывной, так и дискретной случайной величиной.
Состав генеральной совокупности определяется целями исследования. Например, если нас интересует распространенность какого-либо заболевания в некотором регионе, то генеральная совокупность – все население региона. Если же мы хотим выяснить подверженность этому заболеванию мужчин и женщин по отдельности, то следует рассматривать две генеральные совокупности.
Для изучения свойств генеральной совокупности отбирают некоторую часть ее элементов.
Выборка – часть генеральной совокупности, выбираемая для обследования (лечения).
Если это не вызывает недоразумений, то выборкой называют как совокупность объектов, отобранных для обследования, так и совокупность значений исследуемого признака, полученных при обследовании. Эти значения могут быть представлены несколькими способами.
Простой статистический ряд – значения исследуемого признака, записанные в том порядке, в котором они были получены.
Пример простого статистического ряда, полученного при измерении скорости поверхностной волны (м/с) в коже лба у 20 пациентов, приведен в табл. 3.1.
| Простой статистический ряд | Таблица 3.1 | |||||||||||||||||||
| n | ||||||||||||||||||||
| Х |
Просто статистический – основной и самый полный способ записи результатов обследования. Он может содержать сотни элементов. Окинуть такую совокупность одним взглядом весьма затруднительно. Поэтому большие выборки обычно подвергают разбиению на группы. Для этого область изменения признака разбивают на несколько (N) интервалов равной ширины и подсчитывают относительные частоты (ni/n) попадания признака в эти интервалы. Ширина каждого интервала равна:
d = (xmax – xmin)/N.
Границы интервалов имеют следующие значения:
xmin; xmin + d; xmin + 2d; ….. xmax
Если какой-то элемент выборки является границей между двумя соседними интервалами, то его относят к левому интервалу. Сгруппированные таким образом данные называют интервальным статистическим рядом.
Интервальный статистический ряд – это таблица, в которой приведены интервалы значений признака и относительные частоты попадания признака в эти интервалы.
В нашем случае можно образовать, например, такой интервальный статистический ряд (N = 5, Dх = 4), табл. 3.2:
| Интервальный статистический ряд | Таблица 3.2 | |||||
| х, х+Dх | 28–32 | 32–36 | 36–40 | 40–44 | 44–48 | |
| Р*= ni/n | 0,10 | 0,25 | 0,40 | 0,15 | 0,10 | |
Здесь к интервалу 28–32 отнесены два значения равные 28 (табл. 2), а к интервалу 32–36 – значения 32, 33, 34 и 35.
Интервальный статистический ряд можно изобразить графически. Для этого по оси абсцисс откладывают интервалы значений признака и на каждом из них, как на основании, строят прямоугольник с высотой, равной относительной частоте. Полученная столбчатая диаграмма называется гистограммой.

Рис. 3.1. Гистограмма.
На гистограмме статистические закономерности распределения признака просматриваются достаточно отчетливо. При большом объеме выборки (несколько тысячь) и малой ширине столбцов форма гистограммы близка к форме графика плотности распределения признака.
Число столбцов гистограммы можно выбрать по следующей формуле:
N = 1 + 3,3×lg n. (3.1)
Построение гистограммы вручную – процесс долгий и нудный. Поэтому разработаны компьютерные программы для автоматического построения.
Числовые характеристики статистического ряда
Многие статистические проце6дуры используют выборочные оценки для математического ожидания и дисперсии (или СКО) генеральной совокупности.
Выборочное среднее (  ) есть среднее арифметическое всех элементов простого статистического ряда:
) есть среднее арифметическое всех элементов простого статистического ряда:
 . (3.2)
. (3.2)
Для нашего примера  = 37,05 (м/с).
= 37,05 (м/с).
Выборочное среднее – это наилучшая оценка математического ожидания (М) генерального среднего.
Выборочная дисперсия s2 равна сумме квадратов отклонений элементов от выборочного среднего, поделенной на n – 1 :
 . (3.3)
. (3.3)
В нашем примере s2 = 25,2 (м/с)2.
Обратите внимание, что при вычислении выборочной дисперсии в знаменателе формулы стоит не объем выборки n, а n-1. Это связано с тем, что при вычислении отклонений вместо неизвестного математического ожидания используется его оценка – выборочное среднее.
Выборочная дисперсия – это наилучшая оценка генеральной дисперсии (s2).
Выборочное среднеквадратическое отклонение (s) – это квадратный корень из выборочной дисперсии:
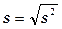 . (3.4)
. (3.4)
Для нашего примера s = 5,02 (м/с).
Выборочное среднеквадратическое отклонение – это наилучшая оценка генерального СКО (s).
|
из
5.00
|
Обсуждение в статье: Числовые характеристики статистического ряда |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

