 |
Главная |
Что необходимо знать и уметь на данный момент?
|
из
5.00
|
– Вы должны ПОНИМАТЬ, что такое предел функции. Не выучить, не зазубрить, а именнопонять хотя бы на общем, интуитивном уровне. Поэтому, если пределы сродни китайской грамоте, пожалуйста, начните с базового урока Пределы. Примеры решений, а также загляните в справку Графики и свойства элементарных функций, где я проиллюстрировал геометрический смысл понятия.
– Необходимо уметь использовать основные методы решения пределов и справляться с наиболее распространёнными заданиями. Очень хорошо, если кроме примеров моих первых двух уроков, вы порешали (или попытались порешать) что-нибудь дополнительно.
Есть? Едем дальше. Начнём с пары вопросов, которые вызвали недопонимание у некоторых посетителей сайта. За 2 года в отзывах и личной переписке мне удалось выяснить те моменты, которые недостаточно подробно рассмотрены в ранних статьях. И сейчас самое время акцентировать на них внимание.
Первый вопрос затрагивает саму сущность предела. В черновой версии урока я даже процитировал Винни-Пуха: «Куда идём мы с Пятачком, большой-большой секрет». Но потом убрал… нехорошо как-то… выходит все, кто этого не понял – медведи с опилками в голове.
«Чему равен предел  ?» (пример условный)
?» (пример условный)
Действительно, чему?
Здесь не указано, куда стремится «икс», и такая запись не имеет смысла:

Предел функции не летает где-то по воздуху на воздушном шаре, он может существовать (или не существовать) только в определённой точке (в частности, в точке  или
или 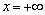 ). Например:
). Например:

Заодно вспоминаем примитивный, но важный приём – чтобы вычислить предел, сначала нужно попытаться подставить значение «икс» в функцию. В случае с бесконечностью очевидно, что:

Иными словами, если  , то функция
, то функция  неограниченно возрастает.
неограниченно возрастает.
А вот следующего предела не существует:

Значение  не входит в область определения функции (под корнем получается «минус»).
не входит в область определения функции (под корнем получается «минус»).
рАвно не существует и такого предела:

Тут «икс» стремится к «минус бесконечности», и под корнем нарисуется бесконечно большоеотрицательное число.
Итак, в природене существует «просто предела». Предел может существовать (или не существовать) лишь в определённой точке, в частности, в точке «плюс бесконечность» или «минус бесконечность».
В процессе оформления практических примеров постарайтесь придерживаться следующей рекомендации: не допускайте неполной записи вроде  , это одна из самых скверных оплошностей. Презумпция виновности студента утверждает, что он либо совсем не в теме, либо откуда-то впопыхах списал пример.
, это одна из самых скверных оплошностей. Презумпция виновности студента утверждает, что он либо совсем не в теме, либо откуда-то впопыхах списал пример.
Второй вопрос касается путаницы с неопределённостями, которые возникают в ходе решения более сложных пределов. Систематизируем информацию:
Что в пределах функций ЯВЛЯЕТСЯ неопределённостью
и НЕ ЯВЛЯЕТСЯ неопределённостью
Прежде всего, перед решением любого предела, обязательно выполняем подстановку «икса» в функцию – неопределённости может и не быть! Однако сладостей много вредно, и на первых двух уроках мы сталкивались со следующими неопределённостями:

Кроме указанных видов, существует довольно распространённая неопределённость  («бесконечность минус бесконечность»), которую мы подробно разберём в этой статье, и совсем редко встречаются неопределённости
(«бесконечность минус бесконечность»), которую мы подробно разберём в этой статье, и совсем редко встречаются неопределённости 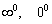 .
.
Для того чтобы устранить неопределённость, как вы знаете, необходимо использовать некоторые правила и методы решения пределов.
Теперь о том, ЧТО НЕ ЯВЛЯЕТСЯ неопределённостью.
Неопределённостью не является:
– Любая определённость =)
– Бесконечно малое число, делённое на ненулевую константу:  . Сюда же можно отнестибесконечно малое число, делённое на бесконечно большое число:
. Сюда же можно отнестибесконечно малое число, делённое на бесконечно большое число: 
– Ненулевая константа, делённая на бесконечно малое число, например:  .
.
– Начинающие изучать математический анализ, часто пытаются устранить мифическую неопределённость  . Но все попытки тщетны, поскольку это определённость:
. Но все попытки тщетны, поскольку это определённость:
представим «бесконечность делить на ноль» в виде произведения:  , и, согласно предыдущему пункту:
, и, согласно предыдущему пункту:  . Приведу живой пример:
. Приведу живой пример:

Примечание: знак  можно записать и без «плюса»:
можно записать и без «плюса»:  . Это равноценные обозначения, и на практике используют оба варианта. Для более чёткого изложения в ряде примеров я буду ставить знак «плюс».
. Это равноценные обозначения, и на практике используют оба варианта. Для более чёткого изложения в ряде примеров я буду ставить знак «плюс».
– Число, не равное единице, в бесконечно большой степени не является неопределённостью. Например:  . В частности:
. В частности: 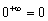 .
.
– Разность двух функций, каждая из которых стремится к нулю, например:  . Таким образом, неопределённости «ноль минус ноль» тоже не существует – это определённость.
. Таким образом, неопределённости «ноль минус ноль» тоже не существует – это определённость.
Многие из перечисленных неопределённостей и определённостей уже встречались и ещё неоднократно встретятся на практике.
До нового 2013-го года остаются считанные дни, и в качестве подарка я принёс увесистый ящик с петардами:
Порядок роста функции
В данном параграфе будут разобраны пределы с многочленами, многочленами под корнем, когда  или
или 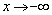 . Материал вам уже частично знаком, и настала пора разобраться в нём как следует. Давайте научимся находить решение в считанные секунды!
. Материал вам уже частично знаком, и настала пора разобраться в нём как следует. Давайте научимся находить решение в считанные секунды!
Вычислим следующий предел:

На базовом уроке Пределы. Примеры решений я рекомендовал рассуждать не совсем корректным способом: сначала «икс» равно 10, потом, 100, затем 1000, миллион и т.д. до бесконечности. В чём изъян такого подхода? Построим данную последовательность:
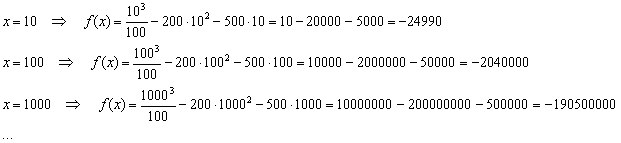
Исходя из полученных результатов, складывается стойкое впечатление, что предел стремится к «минус бесконечности»:

Но на поверку впечатление кардинально ошибочно. В этой связи необходимо знать теорию матана, а именно, некоторые выкладки о порядке роста функции.
Применительно к нашему примеру можно сказать, что слагаемое  обладает более высоким порядком роста, чем сумма
обладает более высоким порядком роста, чем сумма  . Иными словами, при достаточно больших значениях «икс» слагаемое
. Иными словами, при достаточно больших значениях «икс» слагаемое  «перетянет» на «плюс бесконечность» всё остальное:
«перетянет» на «плюс бесконечность» всё остальное:
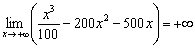
При небольших значениях «икс» – да, сладкая парочка  перетягивает канат в сторону «минус бесконечности», что и привело нас к неверному первоначальному выводу. Но уже при
перетягивает канат в сторону «минус бесконечности», что и привело нас к неверному первоначальному выводу. Но уже при  получается гигантское положительное число
получается гигантское положительное число  .
.
Если сильно уменьшить первое слагаемое, то от этого ничего не изменится:  , будет лишь отсрочен тот момент, когда бравая дробь
, будет лишь отсрочен тот момент, когда бравая дробь  «вытянет» весь предел на «плюс бесконечность». Не поможет и «усиление противовеса»:
«вытянет» весь предел на «плюс бесконечность». Не поможет и «усиление противовеса»:
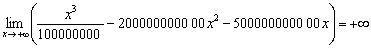 .
.
Нулей можете приписать, сколько хотите (без шуток). Удивительная наука математический анализ – способна низвести любого монстра до мелочи пузатой.
Таким образом, кубическая функция имеет более высокий порядок роста, чем:
– квадратичная функция;
– линейная функция;
– функция-константа;
– сумма квадратичной функции, линейной функции и константы (в любых комбинациях).
На простейшем примере поясню геометрический смысл вышесказанного. Представьте графики линейной  , квадратичной
, квадратичной  и кубической
и кубической  функций (см. методичку Графики и свойства функций). Легко заметить, что при увеличении значений «икс», кубическая парабола
функций (см. методичку Графики и свойства функций). Легко заметить, что при увеличении значений «икс», кубическая парабола  взмывает вверх гораздо быстрее и круче, чем парабола и, тем более, прямая.
взмывает вверх гораздо быстрее и круче, чем парабола и, тем более, прямая.
Аналогичное правило можно сформулировать для любой степени:
Степенная функция данной степени растёт быстрее, чем любая степенная функция более низкой степени. И быстрее, чем сумма любого количества степенных функций более низкой степени.
Найдём предел 
Значение данного предела зависит только от слагаемого  . Всё остальное МЫСЛЕННО отбрасываем:
. Всё остальное МЫСЛЕННО отбрасываем:  , и теперь ясно как день, что предел стремится к «минус бесконечности»:
, и теперь ясно как день, что предел стремится к «минус бесконечности»:
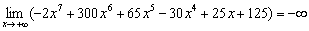
То есть, слагаемое  более высокого порядка роста, чем всё остальное.
более высокого порядка роста, чем всё остальное.
У «хвоста»  могут быть сколь угодно большие константы, другие знаки, но результат от этого НЕ ИЗМЕНИТСЯ.
могут быть сколь угодно большие константы, другие знаки, но результат от этого НЕ ИЗМЕНИТСЯ.
|
из
5.00
|
Обсуждение в статье: Что необходимо знать и уметь на данный момент? |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

