 |
Главная |
Преобразование нелинейной модели к сепарабельному виду. Аппроксимация нелинейной сепарабельной функции кусочно-линейной функцией
|
из
5.00
|
Y=36x2-5x12+4x1x2-5x22 → max
При ограничениях:
x1+x2 ≤ 2
x1 ≤ 1/2
x1,2 ≥ 0
Функция является сепарабельной, если ее можно представить как сумму функций, каждая из которых зависит от одной переменной. Целевая функция данной задачи не является сепарабельной, т.к. содержит произведение двух переменных  . Для приведения ее к сепарабельному виду необходимо ввести подстановку
. Для приведения ее к сепарабельному виду необходимо ввести подстановку 
В задачу также добавятся ограничения:
y1=1/2*x1+1/2*x2
z2=1/2*x1+1/2*x2
y2-z2≥0
Тогда задача примет вид:


Определим верхние и нижние границы переменных х1, х2, z, y. Для этого решаем соответствующие задачи линейного программирования. В итоге получим:
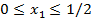


 /4
/4
Для осуществления линеаризации выберем некоторую «сетку» значений x, построенную так:

Затем любое значение x будем выражать в виде некоторой средневзвешенной xk по правилу:

где веса lk удовлетворяют условиям:


Для выбора точек аппроксимации построим графики линеаризуемых функций.

Рисунок 3.1 - 

Рисунок 3.2 - 

Рисунок 3.3 - 
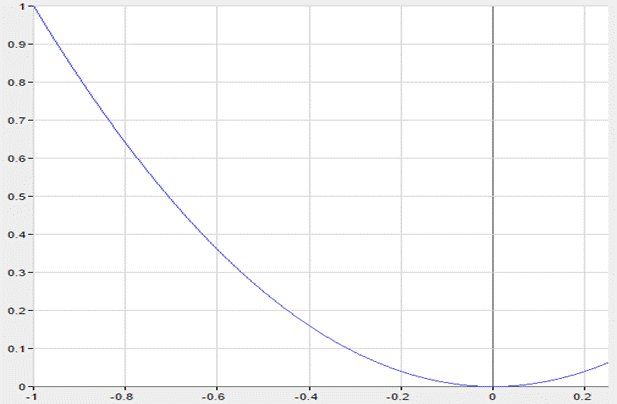
Рисунок 3.4 - 
Точки следует выбрать в соответствии со следующим правилом: чем менее линейна функция на определенном участке, тем выше должна быть плотность точек аппроксимации. Разбиения, принятые при решении данной задачи, приведены в таблице 3.3.1.
Таблица 3.3.1 – Сетка аппроксимации
| Переменная | Номера точек | |||||||||
| x1 | 1/18 | 1/9 | 1/6 | 2/9 | 5/18 | 1/3 | 7/18 | 4/9 | 1/2 | |
| x2 | 2/9 | 4/9 | 2/3 | 8/9 | 10/9 | 4/3 | 14/9 | 16/9 | ||
| y1 | 1/9 | 2/9 | 1/3 | 4/9 | 5/9 | 2/3 | 7/9 | 8/9 | ||
| z1 | -1 | -7/8 | -3/4 | -5/8 | -1/2 | -3/8 | -1/4 | -1/8 | 1/4 |
Выразим переменные
Таблица 3.3.2
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | U10 | ||
| x1 | 1/18 | 1/9 | 1/6 | 2/9 | 5/18 | 1/3 | 7/18 | 4/9 | 1/2 | ||
| f(x1) | -5/324 | -5/81 | -5/36 | -20/81 | -125/32 | -5/9 | -245/32 | -80/81 | -5/4 | ||
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | ||
| x2 | 2/9 | 4/9 | 2/3 | 8/9 | 10/9 | 4/3 | 14/9 | 16/9 | |||
| f(x2) | 628/81 | 1216/81 | 196/9 | 2272/81 | 2740/81 | 352/9 | 3556/81 | 3904/86 | |||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | ||
| y | 1/9 | 2/9 | 1/3 | 4/9 | 5/9 | 2/3 | 7/9 | 8/9 | |||
| f(y) | 1/81 | 4/81 | 1/9 | 16/81 | 25/81 | 4/9 | 49/81 | 64/81 | |||
| T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | ||
| z | -1 | -7/8 | -3/4 | -5/8 | -1/2 | -3/8 | -1/4 | -1/8 | 1/4 | ||
| f(z) | 49/64 | 9/16 | 25/64 | 1/4 | 9/64 | 1/16 | 1/64 | 1/16 | |||




Решение задачи сепарабельным симплекс-методом
Теперь, используя выбранные точки можно преобразовать нелинейные ограничения и нелинейную ЦФ к кусочно-линейному виду. К ограничениям также добавятся ограничения, обеспечивающие свойство весов смежных точек. В итоге получим задачу линейного программирования.
Максимизировать целевую функцию вида:

При ограничениях:



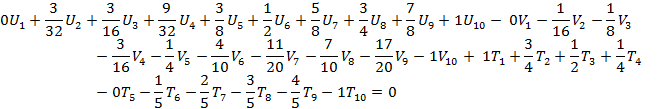

k = 1, 2, …, 10.
Полученную задачу решаем с помощью сепарабельного симплекс-метода. Сепарабельный симплексный алгоритм аналогичен обычному симплекс методу, за исключением необходимости соблюдения правила ограниченного ввода в базис, суть которого заключается в том, что оптимальное решение, полученное с использованием аппроксимирующей модели, содержит либо один вес lk, либо два соседних lk, lk+1.
Оптимизация исходной целевой функции и ее решение, с учетом правила ограниченного ввода в базис, приведены в приложении B.
Полученследующийрезультат:





Подставим полученные значения в исходную функцию и ограничения, получим:


Y = 21/5
Ответ:X = (1; 4/5); Y = 21/5
|
из
5.00
|
Обсуждение в статье: Преобразование нелинейной модели к сепарабельному виду. Аппроксимация нелинейной сепарабельной функции кусочно-линейной функцией |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

