 |
Главная |
Тригонометрическая форма рядов Фурье
|
из
5.00
|
Комплексное ДПФ
До сих пор мы рассматривали ДПФ от действительных сигналов. Обобщим те-перь ДПФ на случай комплексных сигналов. Пусть x[n], n=0,…,N-1 – исходный комплексный сигнал, состоящий из N комплексных чисел. Обозначим X[k], k=0,…N-1 – его комплексный спектр, также состоящий из N комплексныхчи-сел. Тогда справедливы следующие формулы прямого и обратного преобразо-ваний Фурье (здесь 1−=j):

Если по этим формулам разложить в спектр действительный сигнал, то первые N/2+1 комплексных коэффициентов спектра будут совпадать со спектром «обычного» действительного ДПФ, представленным в «комплексном» виде, а остальные коэффициенты будут их симметричным отражением относительно половины частоты дискретизации. Для косинусных коэффициентов отражение четное, а для синусных – нечетное.
Двумерное ДПФ
Для изображений, представляющих собой двумерный сигнал, спектром являет-ся также двумерный сигнал. Базисные функции преобразования Фурье имеют вид

причем фазы также могут быть раз-личны. На изображении каждая из этих базисных функций представляют собой волну определенной частоты, определенной ориентации и определенной фазы.
Здесь N1xN2 – размер исходного сигнала, он же – размер спектра. k1 и k2 – это номера базисных функций (номера коэффициентов двумерного ДПФ, при ко-торых эти функции находятся). Поскольку размер спектра равен размеру ис-ходного сигнала, то k1 = 0,…,N1-1; k2 = 0,…,N2-1.
Непосредственное вычисление двумерного ДПФ по приведенным формулам требует огромных вычислительных затрат. Однако можно доказать, что дву-мерное ДПФ обладает свойством сеперабельности, т.е. его можно вычислить последовательно по двум измерениям. Для вычисления двумерного ДПФ дос-таточно вычислить одномерные комплексные ДПФ всех строк изображения, а затем вычислить в результирующем «изображении» одномерные комплексные ДПФ всех столбцов. При этом результаты всех одномерных комплексных ДПФ нужно записывать на место исходных данных для этих ДПФ. Например, при вычислении одномерного ДПФ первой строки изображения нужно результат ДПФ записать в первую строку этого изображения (он имеет тот же размер). Для этого нужно каждый «пиксель» хранить в виде комплексного числа.
Ряды Фурье
Разложению в ряды Фурье подвергаются периодические сигналы. Периодическую функцию любой формы, заданную на интервале одного периода Т = b-a и удовлетворяющую на этом интервале условиям Дирехле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1-го рода), можно представить в виде ряда Фурье:
s(t) =  Snexp(jnDwt), Sn = S(nDw), Dw = 2p/T, (1)
Snexp(jnDwt), Sn = S(nDw), Dw = 2p/T, (1)
где весовые коэффициенты Sn ряда определяются по формуле:
Sn = (1/T)  s(t) exp(-jnDwt) dt.(2)
s(t) exp(-jnDwt) dt.(2)
Ряд Фурье представляет собой ансамбль комплексных экспонент exp(jnDwt) с частотами, образующими арифметическую прогрессию. Функцию весовых коэффициентов S(nDw) принято называть комплексным спектром периодического сигнала или фурье-образом функции s(t). Спектр периодического сигнала является дискретной функцией, т.к. он определен только для целых значений n с шагом по частоте, обратным периоду: Dw = 2p/Т (или Df = 1/T). Первую частотную составляющую спектра при n = 1, равную w1 = 1×Dw = 2p/T (или f1 = 1/T), называют основной частотой сигнала (первой гармоникой), остальные частоты дискретного спектра nDw при n>1 называют гармониками сигнала. Значения S(nDw) по положительным и отрицательным значениям n являются комплексно сопряженными. Шаг по частоте Dw между двумя соседними синусоидами называется частотным разрешением спектра.
С чисто математических позиций множество функций exp(jnDwt), -¥< n <¥ образует бесконечномерный базис линейного пространства L2[a,b] ортогональных синус-косинусных функций, а коэффициенты Sn по (2) представляют собой проекции сигнала s(t) на эти базисные функции. Соответственно, сигнал s(t) в форме ряда Фурье (1) – это бесконечномерный вектор в пространстве L2[a,b], точка с координатами Sn по базисным осям пространства exp(jnDwt).
Коэффициенты Sn в (2) отображают функцию s(t) в новое пространство единственным образом. Если функция s(t) непрерывна, то ряд (1) сходится равномерно к s(t), при этом ошибка аппроксимации ||s(t)-sN(t)|| функции s(t) с усечением ряда (1) до ±N членов меньше ошибки аппроксимации любым другим рядом с тем же количеством членов. Если s(t) не является непрерывной (имеет разрывы), но конечна по энергии (квадратично интегрируема), то метрика ||s(t)-sN(t)|| стремится к нулю при N → ∞, при этом в точках разрыва сумма ряда стремится к (s(t+)+s(t-))/2.
Тригонометрическая форма рядов Фурье
Объединяя в (1) комплексно сопряженные составляющие (члены ряда, симметричные относительно центрального члена ряда S0), можно перейти к ряду Фурье в тригонометрической форме:
s(t) = Ао+2  (An cos(nDwt) + Bnsin(nDwt)), (6)
(An cos(nDwt) + Bnsin(nDwt)), (6)
s(t) = Ао+  2Rn cos(nDwt + jn). (6')
2Rn cos(nDwt + jn). (6')
Значения An, Bn вычисляются по формулам (4-5), значения Rn и jn - по (3').
Ряд (6) представляют собой разложение периодического сигнала s(t) на сумму вещественных элементарных гармонических функций (косинусных и синусных) с весовыми коэффициентами, удвоенные значения которых (т.е. значения 2An, 2Bn) не что иное, как реальные амплитуды соответствующих гармонических колебаний с частотами nDw. Совокупность амплитудных значений этих гармоник образует односторонний физически реальный (только для положительных частот nDw) спектр сигнала. Для сигнала на рис.1, например, он полностью повторяет правую половину приведенных на рисунке спектров с удвоенными значениями амплитуд (за исключением значения Ао на нулевой частоте, которое, как это следует из (6), не удваивается). Но такое графическое отображение спектров используется довольно редко.

Рис.5 Реконструкция сигнала по ограниченному ряду Фурье.
На рис.6. приведен пример разложения в ряд Фурье одного периода T=(a,c) модельного периодического сигнала sq(x), представленного информационным сигналом s(x) в сумме с шумовым сигналом. Спектр шумов близок к спектру белого шума (равномерное распределение энергии шумов по всем частотам спектра).
На спектре модельного сигнала достаточно четко выделяется диапазон частот информационного сигнала. Реконструкция сигнала с ограничением ряда Фурье гармониками только информационного сигнала (сигнал sr5(x), N=5) дает сглаженную форму сигнала по минимуму среднеквадратического расхождения с модельным сигналом для данного количества членов ряда, но только по периоду разложения (а, с), и наиболее точное приближение к информационному сигналу. При увеличении в реконструкции количества членов ряда Фурье восстановленный сигнал начинает приближаться к модельному сигналу, но только по данному периоду T=(a,c), при этом расхождение с информационным сигналом увеличивается. Заметим, что спектр сигнала может определяться и по нескольким периодам сигнала, что повышает точность реконструкции информационного сигнала.
В ряд Фурье может разлагаться и произвольная непериодическая функция, заданная (ограниченная, вырезанная из другого сигнала, и т.п.) на интервале (a,b), если нас не интересует ее поведение за пределами данного интервала. Однако следует помнить, что применение формул (1-6) автоматически означает периодическое продолжение данной функции за пределами заданного интервала (в обе стороны от него) с периодом Т = b-a.
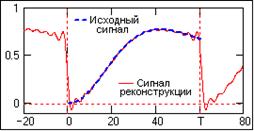
Рис.7.
|
из
5.00
|
Обсуждение в статье: Тригонометрическая форма рядов Фурье |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

