 |
Главная |
Тема 2. Дифференцирование функции
|
из
5.00
|
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 1
Тема 1. Введение в анализ
Задача 1. Вычислить пределы:
а) 
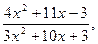 б)
б) 
в)  г)
г) 
Решение. а) Подстановка предельного значения аргумента х=−3 приводит к неопределенному выражению вида 
Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при х  :
:

 =
= 
 =
= 
 =
=
=  =
=  ;
;
б) При  выражение
выражение 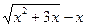 дает неопределенность вида
дает неопределенность вида  −
−  . Для ее устранения умножим и разделим это выражение на (
. Для ее устранения умножим и разделим это выражение на (  ):
):


= 

в) Обозначим 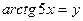 . Тогда
. Тогда  и
и  при
при  . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела  имеем:
имеем:


 ·
· 
=  ·1·1=
·1·1=  ;
;
г) При  выражение
выражение  является неопределенностью вида 1∞. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при
является неопределенностью вида 1∞. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при  величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела:
 .
.
Тогда имеем: 
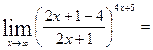 =
= 
Пусть 2х+1= −4у. Тогда 4х+5=−8у+3 и у  −
−  при
при  . Переходя к переменной у, получим:
. Переходя к переменной у, получим:


Тема 2. Дифференцирование функции
Задача 2.Найдите производные функции:
а) у=ln  ;
;
б) у= 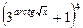 ;
;
в)  .
.
Решение: а) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:
у' =  ' =
' =  '=
'=
= 
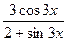 ;
;
б) у'= 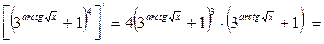
=4 
=4 
 ;
;
в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной у' нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно у':
−sin  −sin
−sin 
−y 
Из последнего уравнения находим у':
2 

Задача 3. Исследовать функцию у= 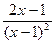 и построить ее график.
и построить ее график.
Решение. Исследование функции проведем по следующей схеме:
1. Найдем область определения функции.
2. Исследуем функцию на непрерывность.
3. Установим, является ли данная функция четной, нечетной.
4. Найдем интервалы возрастания и убывания функции и точки экстремума.
5. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.
6. Найдем асимптоты кривой.
Реализуем указанную схему:
1. Функция определена при всех значениях аргумента х, кроме х=1.
2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах (−∞; 1) и (1; ∞).
3. Для установления четности или нечетности функции проверим выполнимость равенств  =
=  (тогда f(х) – четная функция) или
(тогда f(х) – четная функция) или  =
=  (для нечетной функции) для любых х и −х из области определения функции:
(для нечетной функции) для любых х и −х из области определения функции:
 =
=  ,
,  =−
=− 
Следовательно, 

 и
и 

 , то есть данная функция не является ни четной, ни нечетной.
, то есть данная функция не является ни четной, ни нечетной.
4. Для исследования функции на экстремум найдем ее первую производную:
у'= 
у'=0 при  и у' − не существует при
и у' − не существует при  . Тем самым имеем две критические точки:
. Тем самым имеем две критические точки: 
 Но точка
Но точка 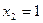 не принадлежит области определения функции, экстремума в ней быть не может.
не принадлежит области определения функции, экстремума в ней быть не может.
Разобьем числовую ось на три интервала (рис. 5): (−∞; 0), (0; 1), (1; ∞).
В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале – положительная и данная функция возрастает. При переходе через точку  первая производная меняет свой знак с минуса на плюс, поэтому в этой точку функция имеет минимум: уmin=y(0)=−1. Значит, А(0; −1) − точка минимума.
первая производная меняет свой знак с минуса на плюс, поэтому в этой точку функция имеет минимум: уmin=y(0)=−1. Значит, А(0; −1) − точка минимума.
На рис. 5 знаками +, −указаны интервалы знакопостоянства производной у', а стрелами – возрастание и убывание исследуемой функции.
5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:
у''=− 

Рис. 5
у''=0 при 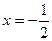 , и у''− не существует при
, и у''− не существует при  . Разобьем числовую ось на три интервала (рис. 6): (−∞; −
. Разобьем числовую ось на три интервала (рис. 6): (−∞; −  ), (−
), (−  ; 1), (1; ∞). На первом интервале вторая производная у''=0, при
; 1), (1; ∞). На первом интервале вторая производная у''=0, при 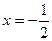 − абсцисса точки перегиба.
− абсцисса точки перегиба.
Следовательно, В 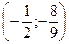 - точка перегиба графика функции.
- точка перегиба графика функции.
 |



Рис. 6
6.  − точка разрыва функции, причем
− точка разрыва функции, причем  .
.
Поэтому прямая  является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты
является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты 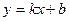 воспользуемся формулами:
воспользуемся формулами:
 ,
,  .
.
Тогда
 ,
,
 .
.
Значит, прямая у=0 есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.
 |
Рис. 7
Задача 4. Найти приближенное значение функции  при значении
при значении 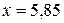 исходя из её точного значения при
исходя из её точного значения при  .
.
Решение: Известно, что дифференциал dy функции y=f(x) представляет собой главную часть приращения этой функции  . Если приращение аргумента
. Если приращение аргумента  мало по абсолютной величине, то приращение
мало по абсолютной величине, то приращение  приближенно равно дифференциалу, т. е.
приближенно равно дифференциалу, т. е.  . Так как
. Так как  , а
, а 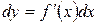 , то имеет место приближенное равенство:
, то имеет место приближенное равенство: 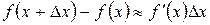 .
.
Пусть  ,
,  Тогда
Тогда
 (1)
(1)
Приближенное равенство (1) дает возможность найти значение функции при  , если известно значение функции и ее производной при
, если известно значение функции и ее производной при  .
.
Прежде чем воспользоваться приближенным равенством (1), находим численное значение производной при  :
:
 или
или 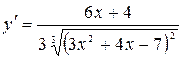 ;
;  .
.
Применяя (1), получаем  .
.
|
из
5.00
|
Обсуждение в статье: Тема 2. Дифференцирование функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

