 |
Главная |
Тема 5. Дифференциальные уравнения
|
из
5.00
|
Задача 8.Решить уравнение у'−у tg x=−y2cos x.
Решение. Данное уравнение является уравнением Бернулли. Для его решения (как и для линейного уравнения) искомую функцию у представим в виде произведения двух других функций: u=u(x) и υ=υ(х), то есть введем подстановку у= u·υ. Тогда у'=u'υ+uυ' и данное уравнение примет вид:
u'υ+uυ'− uυ tg x=− u2 υ2 cos x
или
υ(u'−u tg x)+ uυ'=− u2 υ2 cos x (1)
Выберем функцию u так, чтобы
u'− u tg x=0 (2)
При подобном выборе функции u уравнение (1) примет вид
uυ'==− u2 υ2 cos x или υ'=− u υ2 cos x (3)
Решая (2) как уравнение с разделяющими переменными, имеем:

 tg x d x, ln u=−ln cos x, u=
tg x d x, ln u=−ln cos x, u=  .
.
Здесь производная постоянная С=0. Подставляя найденное значение u в уравнение (3), имеем:
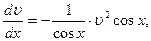

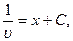
 .
.
Тогда у= u·υ=  − общее решение данного уравнения.
− общее решение данного уравнения.
Задача 9. Найти частное решение уравнения у''+4у=4sin2x-8cos2x, удовлетворяющее начальным условиям у(0)=0, у'(0)=0.
Решение. Общее решение у данного уравнения равно сумме общего решения уодн однородного уравнения и какого-либо частного решения  данного уравнения, то есть
данного уравнения, то есть
у = уодн+  .
.
Для нахождения уодн составим характеристическое уравнение 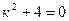 , имеющее комплексные корни
, имеющее комплексные корни  и
и 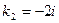 . В этом случае общее решение однородного уравнения ищем в виде
. В этом случае общее решение однородного уравнения ищем в виде
уодн=  , (4)
, (4)
где  − комплексные корни характеристического уравнения. Подставив в (4)
− комплексные корни характеристического уравнения. Подставив в (4)  ,
,  , имеем: уодн=
, имеем: уодн= 
Для нахождения частного решения  неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция
неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция  и числа
и числа  не являются корнями характеристического уравнения, то существует частное решение
не являются корнями характеристического уравнения, то существует частное решение  =
=  . Если же числа
. Если же числа  являются корнями характеристического уравнения, то существует частное решение
являются корнями характеристического уравнения, то существует частное решение  =
=  .
.
Применяя эту теорему при  ,
,  , имеем:
, имеем:  =x(Acos2x+Bsin2x)
=x(Acos2x+Bsin2x)
Дважды дифференцируя последнее равенство, находим у'':
у''=(4В−4Ах) cos2x+(−4А−4Вх) sin2x.
Подставив в данное уравнение  и у'', получим: 4В cos2x−4А sin2x=4 sin2x−8 cos2x,
и у'', получим: 4В cos2x−4А sin2x=4 sin2x−8 cos2x,
откуда А=−1, В=−2.
Следовательно,  =−х(cos2x+2sin2x) и
=−х(cos2x+2sin2x) и
у=  −х(cos2x+2sin2x).
−х(cos2x+2sin2x).
Найдем у':
у'=−2С1 sin2x+2С2 cos2x- cos2x-2sin2x-х(−2sin2x+4 cos2x).
Используя начальные условия, получим систему 
Следовательно, у=  есть искомое частное решение данного дифференциального уравнения.
есть искомое частное решение данного дифференциального уравнения.
Тема 6. Ряды
Задача 10.Написать первыетри члена ряда  , найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
Решение. Беря последовательно n = 1, 2, 3, …, запишем данный ряд в виде:

Для нахождения области сходимости ряда применим признак Даламбера

 .
.
Данный ряд сходится абсолютно при тех значениях x, которые удовлетворяют неравенству  , или
, или  , или
, или  .
.
Исследуем сходимость ряда на концах полученного интервала. При  данный ряд принимает вид
данный ряд принимает вид  .
.
Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при n→ ∞ . Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит,  принадлежит области сходимости данного ряда.
принадлежит области сходимости данного ряда.
При  данный ряд принимает вид
данный ряд принимает вид 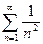 . Это обобщенный гармонический ряд. Так как
. Это обобщенный гармонический ряд. Так как  , то ряд сходится. Значит, при x =
, то ряд сходится. Значит, при x =  исходный ряд сходится.
исходный ряд сходится.
Таким образом,  - область сходимости данного ряда .
- область сходимости данного ряда .
Задача 11.Вычислить 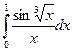 с точностью до 0,001.
с точностью до 0,001.
Решение. Представим подынтегральную функцию в виде степенного ряда. Заменив x в разложении функции sin x на  , имеем:
, имеем:
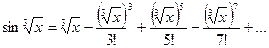
Тогда



 .
.
Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвертый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда
 .
.
|
из
5.00
|
Обсуждение в статье: Тема 5. Дифференциальные уравнения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

