 |
Главная |
Понятие ансамбля систем
|
из
5.00
|
Имеем совокупность макроскопических идентичных систем, именуемых ансамблями. Можем говорить, что конкретная точка фазового пространства соответствует конкретному состоянию одной из систем этого ансамбля.
У систем может быть различное динамическое состояние, так как точки перемещаются в пространстве. Хотя число точек, поля и т.п. у систем будут одинаковыми. Это и будет ансамблем, если таких систем будет неограниченно много.
Часто, т.к. рассматриваются стационарные процессы, то фазовая траектория очень длинная (бесконечная), тогда говорят, что фазовую траекторию, при рассмотрении предела  , можно разбить на достаточно длинные траектории, которым можно приписать системы из ансамбля.
, можно разбить на достаточно длинные траектории, которым можно приписать системы из ансамбля.
Эргодическая гипотеза
Согласно эргодической гипотезе, для наблюдаемых величин в статистической физике водится:

Процессы или поля для которых удовлетворяется это равенство называют эргодическими.
 - это усреднение по пространству реализаций, где
- это усреднение по пространству реализаций, где 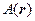 -случайное поле, т.к. здесь больше одной переменной у
-случайное поле, т.к. здесь больше одной переменной у 
 - усреднение по аргументам, которые «сидят» в
- усреднение по аргументам, которые «сидят» в  .
.  - это случайный процесс, т.к. одна переменная в
- это случайный процесс, т.к. одна переменная в  .
.
Равновесное состояние системы
Для стационарных процессов в случае систем с большим числом степеней свободы обнаруживается (где процесс  ), что в процессе измерения величины
), что в процессе измерения величины  , она основное время пребывает в состоянии, имеющим значение близкое к числу
, она основное время пребывает в состоянии, имеющим значение близкое к числу  (которое практически не отлично от
(которое практически не отлично от  ).
).
Система длительное время пребывает в состоянии со значением  . Это значение представляется, таким образом, наиболее вероятным значением случайной величины
. Это значение представляется, таким образом, наиболее вероятным значением случайной величины  .
.
Состояние системы, описываемое наиболее вероятными значениями макропараметра, называется равновесным. Стационарная макросистема основное время пребывает в равновесном состоянии, хотя бывают кратковременные флуктуации.
В термодинамике, во всех термодинамических соотношениях, используются равновесные состояния. Например, под  понимают
понимают  (пишут
(пишут  , а подразумевают
, а подразумевают  ).
).
Время релаксации
Если система выведена из состояния равновесия, то время, в течение которого она, оставленная без воздействия извне, переходит в равновесное состояние, называется временем релаксации  .
.
Если говорят о достаточно больших временах (малых), то обязательно в сравнении с временем  .
.
Достаточно большая макросистема может быть разбита на подсистемы. Так как подсистемы меньше системы, то время релаксации подсистемы меньше времени релаксации всей системы. Так же можно ввести частичные времена релаксации, т.е. времена релаксации по какому-то параметру системы (например, по температуре, по плотности и т.п.).
Можем иметь неполное или частичное равновесие, если рассматриваемы интервал времени 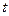 :
:

Здесь 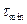 - наименьшее из частичных времен релаксации системы, а
- наименьшее из частичных времен релаксации системы, а 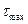 - наибольшее из частичных времен релаксации системы.
- наибольшее из частичных времен релаксации системы.
Неполное равновесие – система по каким-то параметрам пришла в равновесие, а по другим параметрам ещё не пришла в равновесие.
|
из
5.00
|
Обсуждение в статье: Понятие ансамбля систем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

