Статистические методы анализа и моделирования связи

ТЕМА 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Понятие корреляционных и функциональных связей. Методы статистического анализа и моделирования связи.

Однофакторный корреляционно-регрессионный анализ.

Статистическая оценка взаимосвязи между качественными признака с помощью непараметрических методов.

Вопросы для самостоятельного изучения:

- основные предпосылки применения корреляционно-регрессионного анализа;

- простейшие приемы установления связи между признаками;

- многофакторный корреляционно-регрессионный анализ.

Вопрос 1.

Изучение статистических закономерностей – важнейшая задача статистики, которую она решает с помощью особых методов, видоизменяющихся в зависимости от характера исходной информации и целей познания. Знание характера и силы связи позволяет управлять социально-экономическими процессами и предсказывать их развитие. Особую актуальность это приобретает в условиях развивающейся экономики. Изучение механизма рыночных связей, взаимодействия спроса и предложения, влияния объема и структуры товарооборота на объем и состав производства продукции, формирования товарных запасов, издержек производства, прибыли и других качественных показателей имеет первостепенное значение для прогнозирования конъюнктуры рынка, региональной организации производственных и торговых процессов, успешного ведения бизнеса.

Среди многих форм связей важнейшей является причинная, определяющая все другие формы. Сущность причинности состоит в порождении одного явления другим. Вместе с тем, причина сама по себе еще не определяет следствия, она зависит также от условий, вы которых протекает действие причины. Для возникновения следствия нужны все определяющие его факторы – причина и условие. Необходимая обусловленность явлений множеством факторов называется детерминизмом.

Объектами исследования при статистическом измерении связей служит, как правило, детерминированность следствия факторами (причиной и условиями). Признак, характеризующий следствие, называется результативным; признаки, характеризующие причины, - факторными. Выявление связей между признаками основывается на результатах качественного теоретического анализа. Задача статистики – количественная оценка закономерности связей, математическая определенность позволяет использовать результаты экономических разработок для практических целей. Вместе с тем, качественный анализ должен не только предшествовать статистическому, но и являться подтверждением справедливости его результатов.

Между разными явлениями и их признаками необходимо прежде всего выделить два типа связей: функциональную (жестко детерминированную) и стохастическую (стохастически детерминированную).

Связь признака у с признаком х называется функциональной, ели каждому возможному значению независимого признака х соответствует одно или несколько строго определенных значений зависимого признака у.

Характерной особенностью функциональных связей является то, что в каждом отдельном случае известен полный перечень факторов, определяющих значение зависимого (результативного) признака, а также точный механизм их влияния, выраженный определенным уравнением.

Функциональную связь можно представить следующим уравнением:

, (1)

где у_i – результативный признак;

f(x_i) – известная функция связи результативного и факторного признаков;

х_i – факторный признак.

Примером функциональной связи может служить связь между оплатой труда у и количеством изготовленных деталей х при простой сдельной оплате труда. Например, если расценка за одну деталь составляет 3 тыс. рублей, то связь между признаками однозначно выразится простым линейны уравнением у = 3х. Для каждого допустимого значения х можно указать вполне определенное значение у. Если, предположим, х = 5, то соответственно у = 15.

Стохастическая связь – это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины х или других величин х₁, х₂, х₃ и т.д. (случайных или неслучайных) изменением закона распределения. Это обуславливается тем, что зависимая переменная (результативный признак), кроме рассматриваемых независимых, подвержена влиянию ряда неучтенных или неконтролируемых (случайных) факторов, а также некоторых неизбежных ошибок измерения переменных. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.

Характерной особенностью стохастических связей является то, что они проявляются во всей совокупности, а не в каждой ее единице (причем не известен полный перечень факторов, определяющих значение результативного признака, ни точный механизм их функционирования и взаимодействия с результативным признаком). Всегда имеет место влияние случайного.

Модель стохастической связи может быть представлена в общем виде следующим уравнением:

, (2)

где - расчетное значение результативного признака;

f(x_i) – часть результативного признака, сформировавшаяся под воздействием учтенных известных факторных признаков (одного или множества), находящихся в стохастической связи с признаком-результатом;

- часть результативного признака, возникшая вследствие действия неконтролируемых или неучтенных факторов, а также измерения признаков неизбежно сопровождающегося некоторыми случайными ошибками.

Например, уровень производительности труда рабочих стохастически связан с целым комплексом факторов: квалификацией, стажем работы, уровнем механизации или автоматизации производства, интенсивностью труда, простоями и т.д. Полный перечень факторов неизвестен.

Появление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо.

Если ограничится рассмотрением только одного аспекта стохастической связи – изучение вместо условных распределений лишь одного их параметра - условного математического ожидания (среднего значения случайной величины результативного признака), то мы будем исследовать корреляционную или регрессионную связь как частные случаи стохастической связи.

Корреляционная связь существует там, где взаимосвязанные явления характеризуются только случайными величинами. При такой связи среднее значение (математическое ожидание) случайной величины результативного признака у закономерно изменяется в зависимости от изменения другой величины х или других случайных величин х₁, х₂, х₃ и т.д. Корреляционная связь проявляется не в каждом отдельном случае, а во всей совокупности в целом. Только при большом количестве случаев каждому значению случайного признака будет соответствовать распределение средних значений случайного признака у. Таким образом, корреляционная связь является частным случаем стохастической связи.

Кроме того, связи между различными явлениями и их признаками можно классифицировать по следующим признакам.

В зависимости от направленности выделяют прямые и обратные связи.

Прямая связь имеет место тогда, когда направление изменения результативного признака совпадает с изменением направления признака-фактора, т.е. с увеличением факторного признака увеличивается признак результат, и, наоборот, с уменьшением факторного признака уменьшается и результативный признак. Например, чем выше квалификация рабочего (разряд), тем выше уровень производительности труда.

 

Обратная связь имеет место тогда, когда с увеличением факторного признака признак результат уменьшается, или когда с уменьшение значения факторного признак признак-результат увеличивается. Например, чем выше производительность труда, тем ниже себестоимость единицы продукции.

В зависимости от аналитической формы выделяют прямолинейные и криволинейные связи.

Прямолинейные (линейные) связи проявляются тогда, когда с увеличением значения признака-фактора происходит возрастание или уменьшение величины признака-следствия. Математически такая связь выражается уравнением прямой линии:

, (3)

где – теоретические значения результативного признака, полученные по уравнению регрессии;

a₀, a₁ – коэффициенты (параметры) уравнения регрессии.

х – значение признака-фактора.

При криволинейной связи возрастание величины факторного признака оказывает неравномерное влияние на величину результирующего признака. Вначале эта связь может быть прямой, а затем - обратной. Математически такая связь может выражаться рядом функций, например уравнением параболы второго порядка; гиперболы; показательной функции; степенной функции и др.

В зависимости от количества взаимодействующих признаков различают однофакторные и многофакторные связи.

Однофакторные связи обычно называются парными, так какисследуется связь между одним признаком-фактором и одним признаком-результатом (парная корреляция). Например, корреляционная связь между прибылью и производительностью труда.

В случае многофакторной (множественной) связи исследуется влияние многих (два и более) взаимодействующих между собой признаков-факторов на признак-результат (множественная корреляция). Например, корреляционная связь между производительностью труда и уровнем организации труда, автоматизации производства, квалификации рабочих, производственным стажем, простоями и другими факторными признаками. С помощью множественной корреляции можно охватить весь комплекс факторных признаков и объективно отразить существующие множественные связи.

Статистические методы анализа и моделирования связи

Для изучения функциональных связей применяют балансовый и индексный методы статистического анализа.

Для исследованиях корреляционных связей широко используется метод сопоставления параллельных рядов, метод групповой таблицы (или аналитических группировок), графический метод, корреляционно-регрессионный анализ и некоторые непараметрические методы.

Простейшие методы изучения корреляционных связей.

Простейшим приемом обнаружения связи является сопоставление двух параллельных рядов – ряда значений факторного признака и соответствующих ему значений результативного признака. Значение факторного признака (х) располагают в возрастающем порядке и затем прослеживают направление изменения величины результативного признака (у).

В тех случаях, когда возрастание величины факторного признака влечет за собой возрастание и величины результативного признака, говорят о возможном наличии прямой корреляционной связи. Если же с увеличением факторного признака величина результативного признака имеет тенденцию к уменьшению, то можно предполагать обратную связь между признаками.

Однако наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению факторного признака, затрудняет восприятие таких параллельных рядов особенно при большом числе единиц наблюдения. В таких случаях целесообразнее воспользоваться для установления факта наличия связи статистическими групповыми таблицами.

При построении групповой таблицы все наблюдения разбиваются на группы в зависимости от величины признака фактора, и по каждой группе вычисляются средние значения результативного признака (таблица 1).

Таблица 1 – Пример построения групповой таблицы

Группы значений факторного признака х	Частота повторения признака f	Среднее значение результативного признака
Итого

 

Сравнив средние значения результативного признака по группам, можно сделать вывод о наличии связи. Если рост факторного признака влечет за собой рост средних значений результативного признака, то можно предположить наличие прямой корреляционной зависимости между данными признаками.

Корреляционная зависимость отчетливо обнаруживается только при рассмотрении средних значений результативного признака, соответствующих определенным значениям факторного признака, так как при достаточно большом числе наблюдений в каждой группе влияние прочих случайных факторов при расчете групповой средней будет взаимопогашаться, и четче проявиться зависимость результативного признака от фактора, положенного в основу группировки. Иными словами, предполагается, что все прочие причины, если они носят случайный характер, при определении средней по группам взаимопогашаются, т.е. дают в каждой группе один и тот же результат. Следовательно, различия в величине средних будут связаны только с различиями в величине данного факторного признака. Если бы связи между факторным и результативным признаками не было бы, то все групповые средние были бы приблизительно одинаковыми по величине.

Для предварительного выявления связи и раскрытия ее характера, а в известной мере и для выбора формы связи, применяется так же графический метод. Используя данные об индивидуальных значениях признака-фактора и соответствующих ему значениях результативного признака, можно построить в системе прямоугольных координат график, который называется «полем корреляции». Положение каждой точки на графике определяется величиной двух признаков – факторного и результативного. На графике проводят две оси, соответствующие средним значениям признака-фактора и признака-результата . Тогда вся плоскость графика будет разделена на четыре части. Если бы точки, соответствующие значениям признака отдельных единиц, были равномерно распределены по всем четвертям графика, можно было предположить отсутствие связи между признаками.

Если значения факторного признака ниже среднего ( ) и значения результативного признака тоже ниже среднего уровня ( ), или если значения факторного признака выше среднего ( ) и значения результативного признака выше среднего уровня ( ), то в таком случае имеет место прямая корреляционная связь между результативным и факторным признаком.

Рассчитанные с помощью групповой таблицы средние значения результативного признака, соответствующие определенным значениям факторного признака, наносят на график. Соединяя последовательно отрезками прямых соответствующие им точки, получают так называемую эмпирическую линию связи. Если эмпирическая линия связи по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи между признаками. Если же имеет место тенденция неравномерного изменения значений результативного признака и эмпирическая линия связи будет приближаться к какой-либо кривой, то это может быть связано с наличием криволинейной корреляционной связи.

Статистическое моделирование связи

методом корреляционно-регрессионного анализа.

В общем виде задача статистики в области изучения взаимосвязей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа.

Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых, должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на результативный признак.

Задачи регрессионного анализа – выбор типа модели (формы связи), установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной (функции регрессии).

Решение всех названных задач приводит к необходимости комплексного использования этих методов и их объединению в один метод корреляционно-регрессионого анализа.

 

Вопрос 2.

Наиболее разработанной в теории статистики является методология корреляционно-регрессионного анализа парной корреляции, которая исследует связь между одним признаком-фактором (х) и одним признаком-результатом (у).

В основу выявления и установления аналитической формы связи положено применение в анализе исходной информации математических функций, для чего применяют различного вида уравнения прямолинейной и криволинейной связи. Это уравнение называется уравнением регрессии (или уравнение парной зависимости). Например, уравнение парной линейной корреляционной зависимости имеет следующий вид:

, (4)

где у_х – теоретические значения результативного признака, полученные по уравнению регрессии;

a₀, a₁ – коэффициенты (параметры) уравнения регрессии.

Коэффициент парной линейной регрессии а₁ показывает изменение результативного признака у под влиянием изменения факторного признака х. Уравнение (1) показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у, приходящуюся на единицу вариации х. Знак а₁ указывает направление этого изменения.

Параметры уравнения a₀, a₁ определяют путем решения системы нормальных уравнений, полученной на основе метода наименьших квадратов. В основу этого метода положено требование минимальности сумм квадратов отклонений фактических данных (у_i) от выровненных (y_xi):

S(у_i - y_xi)² = S(у_i - а₀ - а₁×х_i)² ® min, (5)

Так, для уравнения парной линейной зависимости система уравнений имеет следующий вид:

(6)

(7)

Параметры уравнения прямой будут иметь следующий вид:

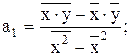(8)

. (9)

Определив значения а₀, а₁ и подставив их в уравнение связи , находим значение у_х, зависящее только от заданного значения х.

Для прямолинейных зависимостей измерителем тесноты связи между признаками является коэффициент парной корреляции, который рассчитывается по формуле:

, (10)

где - среднее произведение факторного и результативного признака:

; (11)

- среднее значение факторного признака:

; (12)

- среднее значение результативного признака:

; (13)

- среднее квадратическое отклонение результативного признака:

; (14)

- среднее квадратическое отклонение факторного признака:

. (15)

Квадрат линейного коэффициента корреляции называется линейным коэффициентом детерминации:

r² = d. (16)

Коэффициент детерминации показывает, какая часть общей вариации результативного признака (y) объясняется влиянием изучаемого фактора (x).

Для получения выводов о практической значимости синтезированных в анализе моделей, показаниям тесноты связи дается качественная оценка. Это осуществляется на основе шкалы Чеддока.

Таблица 9.2 – Шкала Чеддока

Показания тесноты связи	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,999
Характеристика силы связи	слабая	умеренная	заметная	высокая	весьма высокая

 

При r = 1 связь является функциональной, при r= 0 связь отсутствует. Если коэффициент корреляции со знаком «+», то связь прямая, если со знаком «-», то связь обратная.

Для практического использования моделей регрессии важна оценка их адекватности, т.е. соответствия фактическим статистическим данным.

Поскольку корреляционно-регрессионный анализ связи между признаками проводится для ограниченной по объему совокупности, то параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенной статистической модели.

При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения условий: не являются ли полученные значения параметров результатом действия случайных причин.

Значимость параметров простой линейной регрессии осуществляется с помощью t-критерия Стьюдента. При этом вычисляют фактические (расчетные) значения t-критерия:

- для параметра а₀:

, (17)

где - средне квадратическое отклонение результативного признака

у от выровненных значений у_x , которые рассчитываются по уравнению регрессии:

. (18)

- для параметра а₁:

. (19)

Вычисленные по формулам (10.17) и (10.19) значения, сравниваются с критическими t_к, которые принимаются согласно данным таблицы Стьюдента с учетом заданного уровня значимости (a) и числа степеней свободы (k = n – 2). В социально-экономических исследованиях уровень значимости a обычно принимают равным 5%, т.е. a = 0,05, что соответствует доверительной вероятности 95%. Параметр признается существенным при условии, если t_ф > t_к. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.

Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, также могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.

Для оценки значимости линейного коэффициента корреляции r применяется t-критерий Стьюдента. При этом определяется фактическое (расчетное) значение критерия (t_r^ф):

, (20)

где n-2 – число степеней свободы при заданном уровне значимости a и объеме выборки n.

Вычисленное значение t_r^ф сравнивается с критическим t_k , которое берется из таблицы Стьюдента с учетом заданного уровня значимости a и числа степеней свободы k = n - 2.

Если t_r^ф > t_k, то это свидетельствует о значимости линейного коэффициента корреляции r и существенности связи между признаком-фактором и признаком-результатом.

Поскольку не все фактические значения результативного признака лежат на линии регрессии, более справедливо для записи уравнения корреляционной зависимости воспользоваться следующей формулой:

,

где e - отражает случайную составляющую вариации результативного признака.

В некоторых случаях рассеяние точек корреляционного поля настолько велико, что для принятия решений в управлении не целесообразно пользоваться уравнением регрессии, так как погрешность в оценке анализируемого показателя будет чрезвычайно велика. Для всей совокупности наблюдаемых значений рассчитывается средняя квадратическая ошибка уравнения регрессии, которая представляет собой среднее квадратическое отклонение фактических значений результативного признака у относительно значений, рассчитанных по уравнению регрессии у_х:

. (21)

Среднюю квадратическую ошибку уравнения регрессии S_e сравнивают со средним квадратическим отклонением результативного признака s_у. Если S_e < s_у, то использование уравнения регрессии в статистическом анализе является целесообразным.

Таким образом, опираясь на оценку существенности параметров уравнения регрессии и значений линейного коэффициента корреляции, а также на основании оценки надежности уравнения регрессии, дают заключение об адекватности построенной регрессионной модели и возможности распространения выводов, полученных по результатам малой выборки на всю генеральную совокупность.

После проверки адекватности, установления точности и надежности регрессионной модели необходимо ее проанализировать, т.е. дать экономическую интерпретацию параметров регрессии.

Для уравнения парной линейной зависимости прежде всего необходимо проверить согласуется ли знак параметра а₁ с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак. Для удобства интерпретации параметра а₁ следует использовать коэффициент эластичности:

. (22)

Коэффициент эластичности показывает среднее изменение результативного признака при изменении факторного признака на 1% и вычисляется в %-ах.

 

Вопрос 3.

Статистические методы различных обобщений, указывая на наличие прямой или обратной связи между признаком-фактором и признаком-следствием, не дают ответа на вопрос о мере связей, ее количественном выражении. Этот недостаток восполняется методами корреляционного анализа, которые позволяют выделить из комплекса факторов влияние одного или многих обстоятельств, установить характер взаимосвязи и математически точно измерить ее. Все это имеет важное научное и практическое значение. Последовательное внедрение методов измерения в аналитическую практику правоохранительных органов, судов и других юридических учреждений ставит ее на прочную научную основу.

Для изучения корреляционных связей статистиками разработаны разные методы, каждый из которых решает свои конкретные задачи. Одни коэффициенты связи пригодны для измерения взаимосвязей качественных признаков, другие - для качественных и количественных, третьи - для количественных.

Для измерения связи между качественными признаками в статистике широко используются коэффициенты сопряженности А.А. Чупрова, коэффициент ассоциации К. Пирсона, а также коэффициенты ранговой корреляции Спирмена и Кендалла.

Коэффициент ассоциации К. Пирсона (КП) - относительно простой показатель сопряженности величин. Он применяется к вариации двух качественных признаков, распределенных по двум группам.Его расчет производится на основе таблицы, именуемой таблицей четырех полей.

Таблица 10.5 – Расчет коэффициента ассоциации К.Пирсона

Группы	Признаки	Сумма
	а	b	а + b
	с	d	c + d
Сумма	а + с	b + d	-

 

Этими полями являются клетки а, b, с, d. Расчет осуществляется на основе сопряжения по строкама и b, с и d, а также по графам а и с, b u d.

Коэффициент ассоциации Пирсона определяется по формуле:

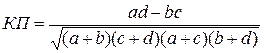(10.37).

Ассоциируемые показатели могут быть как абсолютными, так и относительными. Коэффициент ассоциации измеряется от -1 до +1 и интерпретируется так: чем ближе коэффициент к 1, тем теснее связь.

Пример 10.2. Имеются следующие данные о распределении погибших и раненых по вине водителей и пешеходов за 2003 год (таблица 10.6).

Таблица 10.6 – Распределение погибших и раненых

по вине водителей и пешеходов

Причина наезда	Погибло	Ранено	Сумма
Вина водителей	(а) 15,5%	(b) 84,5%	173 492 100,0 %
Вина пешеходов	(с) 13,8%	(d) 86,2 %	100,0 %
Сумма	29,3 %	186 978 170,7 %	- -

 

Необходимо рассчитать коэффициент ассоциации Пирсона и установить направление и тесноту связи между ранеными и погибшими в дорожно-транспортных происшествиях по вине водителей и пешеходов.

Ввиду того, что абсолютные показатели громоздки, исчислим коэффициент ассоциации Пирсона на относительных показателях, т.е. процентах:

+0,024

Исходя из этого связь между показателями раненых и погибших по вине водителей и пешеходов прямая (+), но незначительная и случайная, поскольку считается, что если коэффициент ассоциации достигает 0,3, то это свидетельствует о существенной связи между признаками.

Коэффициент взаимной сопряженностиА.А. Чупрова (КЧ), в отличие от коэффициента Пирсона, применяется для измерения связи между соотношением двух атрибутивных признаков по трем и более группам. Он рассчитывается по формуле:

, (10.38)

где j ² - показатель взаимного сопряжения;

m₁ и m₂ - число групп по каждому признаку;

1 - постоянный коэффициент.

Коэффициент A.A. Чупрова варьирует от 0 до 1 и его значение не может быть отрицательным. Связь считается существенной при величине коэффициента равной 0,3. Чем ближе его значение к единице, тем сильнее связь.

Пример 10.3. Имеются следующие данные о распределении некоторых преступлений в регионе по видам и их раскрываемости. По таблице 10.7 необходимо рассчитать коэффициента взаимной сопряженности Чупрова и установить направление и тесноту связи между видами преступлений и их раскрываемостью в регионе.

Таблица 10.7 – Распределение некоторых преступлений в регионе

по видам их раскрываемости

Виды преступлений	Раскрыто преступлений	Не раскрыто преступлений	Итого
Разбой
Мошенничество
Умышленное убийство
Поджог
Итого

В нашем примере m₁ - число видов деяний, равное 4 (разбой, мошенничество, умышленное убийство и поджог), m₂ - число групп по раскрываемости преступлений (раскрытые, нераскрытые преступления), равное 2.

Для расчета показателя взаимного сопряжения (j²) построим таблицу 10.8.

Раскроем значение каждого показателя таблицы 10.8 и способы его получения на примере разбоев.

В первой строке каждой клетки (кроме итоговой графы) указаны абсолютные числа раскрытых и нераскрытых преступлений (f_i) (разбой, мошенничество и т. д.). Применительно к разбоям (f₁): раскрыто 110 деяний, не раскрыто 40.

Во второй строке каждой клетки (кроме итоговой графы) указаны квадраты частот преступлений (f_i²). Применительно к разбоям (f₁²): 110 раскрытых деяний в квадрате составляет 12100, а 40 нераскрытых в квадрате составляет 1600.

В третьей строке каждой клетки (кроме итоговой графы) указаны частные от деления квадратов частот на сумму частот по графам (f_i²:Sf). Применительно к раскрытым разбоям (f₁²:Sf): 12100:350=34,5714 и применительно к нераскрытым: 1600:150=10,6667.

 

 

Таблица 10.8 – Количество преступлений в регионе по видам их раскрываемости

Виды преступлений	Раскрыто преступлений	Не раскрыто преступлений	Итого
Разбой f1 f12 f12: Sf (S (f12: Sf )):S f1	34,5714 -	10,6667 -	- 45,2381 0,3016
Мошенничество f2 f22 f22: Sf (S (f22: Sf )):S f2	32 400 92,5714 -	28,1667 -	- 120,7381 0,4928
Умышленное убийство f3 f32 f32: Sf (S (f32: Sf )):S f3	7,1429 -	4,1667 -	- 11.3096 0,1508
Поджог f4 f42 f42: Sf (S (f42: Sf )):S f4	0.2857 -	2,6667 -	- 2,9524 0,0984
Итого Sf S (S (fi2: Sf )):S fi	-	-	1,0436

 

Каждая клетка итоговой графы состоит из четырех строк:

- в первой строке даны суммы частот (110 раскрытых разбоев + 40 нераскрытых = 150);

- во второй строке - прочерк, так как квадраты частот не суммируются;

- в третьей строке даны суммы частных от деления квадратов частот на суммы частот раскрытых и нераскрытых деяний, применительно к разбою: 34,5714 (раскрытые) + 10,6667 (нераскрытые) =45,2381;

- в четвертой строке дается отношение сумм частных (указанных в предыдущей третьей строке) к общему числу частот (указанных в первых строках каждой клетки) ((S(f_i²:Sf)):Sf_i), применительно к разбою ((S(f₁²:Sf)):Sf₁): 45,2381:150 =0,316.

В итоговой строке итоговой графы приводятся два числа: первое - общее число частот (Sf) и второе - общая сумма отношений, указанных в четвертой строке предыдущих клеток итоговой графы (S(S(f_i²:Sf)):Sf_i = 0,3016 + 0,4928 + 0,1508 + 0,984 = 1,0436).

Результирующее число 1,0436, вобравшее в себя все статистически значимые отношения, за вычетом единицы, т.е. 1,0436 - 1 = 0,0436, является именно показателем j², указывающим на взаимную сопряженность атрибутивных признаков нескольких групп.

Тогда коэффициента взаимной сопряженности составит:

.

Коэффициент взаимной сопряженности составил 0,15, что свидетельствует о наличии относительно заметной, но не сильной связи между видами преступлений и их раскрываемостью в регионе.

Особая роль в выявлении связей не только между качественными, но и количественными признаками принадлежит параллельным статистическим рядам. Параллельные статистические ряды представляют собой сопоставление двух и более статистических вариационных или динамических рядов показателей, связанных между собой. Они дают возможность не только увидеть изменения одного явления в рядах распределения, но и установить взаимос