РОЛЬ НАЧАЛЬНЫХ УСЛОВИЙ

Векторное уравнение движения материальной точки можно записать в координатной форме:

, , .

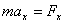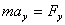(2.6)

Эти три скалярных уравнения, эквивалентные одному векторному уравнению, являются дифференциальными, то есть в них входят вторые производные от координат по времени , поэтому их недостаточно для однозначного описания движения материальной точки. Для однозначного описания движения точки к уравнениям движения надо присоединить дополнительные данные, определяющие значения шести числовых постоянных, получающихся при решении уравнений (2.6), в которые входят вторые производные. В качестве таковых обычно берут значения pадиус-вектора и скорости в момент времени . Эти значения называются начальными условиями.

Поясним этот вопрос на примере движения материальной точки под действием силы тяжести . Уравнение движения в этом случае запишется следующим образом:

.

(2.7)

Это уравнение эквивалентно двум уравнениям:

, .

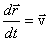Легко проверить, что этим уравнения удовлетворяют следующие решения:

, ,

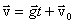(2.8)

где и 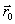– произвольные постоянные векторы. Убедиться в этом можно, если взять производные от и 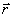по времени. Решение (2.8) называется общим решением уравнения (2.7). Общее решение – это, в сущности, не одно решение, а целое семейство решений, зависящих от двух произвольных векторных постоянных 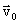и 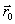. Придавая этим постоянным какие-либо конкретные значения, мы выделяем из этого семейства определенное частное решение. Постоянная 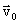– начальная скорость движущейся точки, 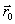– ее радиус-вектор в начальный момент времени. 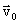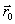Величины и определяются начальными условиями. В зависимости от их значений движения могут сильно отличаться друг от друга: тело может двигаться вверх или вниз по прямой линии, может описывать параболу, достигая или не достигая ее вершины. Получается довольно разнообразный класс движений. Заслуга Ньютона и состоит в том, что он подметил, что все многообразие движений может быть описано единой формулой, не содержащей никаких произвольных постоянных, если от положений и скоростей материальной точки перейти к ее ускорению.

ТРЕТИЙ ЗАКОН НЬЮТОНА

Третий закон Ньютона формулируется следующим образом: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.

.

Одну из сил, или , согласно Ньютону иногда называют действием, а другую – противодействием. Третий закон Ньютона иначе называют законом действия и противодействия. «Если кто нажимает пальцем на камень, – писал Ньютон, – то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и обратно (если можно так выразиться) она с равным усилием оттягивается к камню...». Всякому действию соответствует равное и противоположно направленное противодействие (рис.2.7). Следует, однако, заметить, что «действие» по своей природе ничем не отличается от «противодействия». Так, тяжелое тело, лежащее на столе, давит на стол, испытывая со стороны стола противоположно направленное противодействие. Действие – давление камня на стол – обусловлено деформацией камня, противодействие – давление стола на камень – обусловлено деформацией стола. В основе подразделения сил на «действующие» и «противодействующие» лежит представление об активных телах, производящих действие, и пассивных телах, оказывающих противодействие. Так, если мы поднимаем груз за нитку, то активным телом, производящим действие, будем мы сами, а пассивным телом, оказывающим противодействие, будет груз. Однако подразделение тел на активные и пассивные можно провести далеко не всегда. Например, когда Солнце и планета притягиваются друг к другу силами всемирного тяготения, то в этом взаимодействии они выступают совершенно равноправно, и нельзя указать, какое из взаимодействующих тел является активным, а какое – пассивным. Какую из сил, 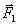или , назвать действием, а какую – противодействием, – это в большинстве случаев вопрос соглашения.

Обосновывая равенство сил действия и противодействия, Ньютон писал: «Относительно притяжений дело может быть изложено вкратце следующим образом: между двумя взаимно притягивающимися телами надо вообразить помещённым какое-либо препятствие, мешающее их сближению. Если бы одно из тел А притягивалось бы телом В сильнее, нежели тело В притягивается телом А, то препятствие испытывало бы со стороны тела А большее давление, нежели со стороны тела В и, следовательно, не осталось бы в равновесии. Преобладающее давление вызвало бы движение системы, состоящей из двух тел и препятствия, в сторону тела В, и в свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону, по которому система должна бы оставаться в своём состоянии покоя или равномерного и прямолинейного движения. Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же».

В основу третьего закона Ньютона положено ньютоновское допущение о мгновенном распространении взаимодействия, которое носит название принципа дальнодействия в классической механике. Согласно этому принципу взаимодействие между телами распространяется в пространстве с бесконечно большой скоростью. Иначе говоря, если изменить состояние одного тела, то сразу же можно обнаружить хотя бы очень слабое изменение во взаимодействующих с ним телах, как бы далеко они не находились.

Сейчас мы знаем, что в действительности это не так – существует конечная максимальная скорость распространения взаимодействий, которая равна скорости света в вакууме. Поэтому третий закон Ньютона (а также и второй) имеет определенные границы применимости.

Примеры

	Баскетболист, забивший мяч, завис на кольце. Противодействующей силе упругости, действующей на спортсмена со стороны кольца, является сила упругой деформации кольца, действующая на кольцо со стороны спортсмена и приложенная к кольцу. Противодействующей силе тяжести, действующей на спортсмена, будет сила гравитационного притяжения Земли баскетболистом, приложенная к Земле
	Сила, с которой самосвал действует на троллейбус при столкновении, равна силе, с которой троллейбус действует на самосвал. При этом последствия действия этих сил для самосвала и троллейбуса могут сильно отличаться. Но ведь в третьем законе Ньютона речь идет только о равенстве сил действия и противодействия, но ничего не говорится о последствиях этого взаимодействия
	Сила, действующая на спортсмена со стороны строп парашюта, равна по величине силе, действующей на стропы со стороны спортсмена
	Сила, с которой спортсмен действует на штангу, и сила, с которой штанга действует на спортсмена, равны по величине и противоположны по направлению. Эти силы приложены к разным телам. Сила, действующая на штангу со стороны спортсмена, уравновешена силой тяжести штанги. Сила, действующая на спортсмена со стороны штанги, в сумме с силой тяжести и силой нормальной реакции опоры, действующими на спортсмена, дают ноль. В результате и штанга, и спортсмен в рассматриваемый момент времени покоятся
	На спортсмена и на катер действуют со стороны соединяющего их каната силы натяжения, равные по величине и противоположные по направлению. Под действием результирующих сил, действующих на катер и спортсмена, эти тела могут двигаться с разными скоростями, ускорениями и в разных направлениях

2.7. ВТОРОЙ ЗАКОН НЬЮТОНА
ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, можно разделить на внутренние и внешние. Внутренними называются силы, с которыми на данное тело воздействуют остальные тела системы; внешними – силы, обусловленные воздействием тел, не принадлежащих системе. В случае если внешние силы отсутствуют, система называется замкнутой или изолированной.

Во Вселенной не может быть полностью изолированных систем, поскольку все тела взаимодействуют между собой. Однако при определенных условиях можно тело считать в достаточной степени изолированным. Например, материальное тело в некоторой области космического пространства, достаточно удаленной от массивных космических тел, ведет себя как изолированная система. В других случаях движение системы в определенных направлениях можно рассматривать как движение замкнутой системы, хотя в целом система таковой не является.

Третий закон Ньютона мы сформулировали для замкнутой системы, состоящей из двух материальных точек. Постулируем теперь его справедливость для системы из произвольного числа материальных точек. Пусть – сила, с которой k-я точка системы действует на i-ю, а – сила, с которой i-я точка действует на k-ю. Третий закон Ньютона утверждает, что обе эти силы направлены вдоль прямой, соединяющей взаимодействующие точки, причем

.

Это соотношение позволяет выполнить переход от механики отдельной материальной точки к механике системы материальных точек.

Пусть в системе из N взаимодействующих частиц кроме внутренних сил 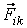на -ю частицу действуют внешние силы, результирующая которых равна 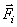. Запишем уравнение движение для каждой из N частиц, входящих в систему:

Сложим правые и левые части этих уравнений. Так как , то

.

Заметим, что импульс системы материальных точек является величиной аддитивной, то есть импульс системы материальных точек равен сумме импульсов отдельных точек, входящих в систему, независимо от того, взаимодействуют они между собой или нет:

,

где – импульс -й частицы. Тогда

.

(2.9)

Согласно полученному уравнению, импульс системы материальных точек может меняться только под действием внешних сил. Внутренние силы исключаются третьим законом Ньютона, поэтому внутренние силы не могут изменить импульс системы. Уравнение (2.9) является обобщением уравнения движения для одной материальной точки.

Таким образом, производная по времени от импульса системы материальных точек равна геометрической сумме всех внешних сил, действующих на систему.

2.8. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК

В любой системе частиц имеется одна замечательная точка, называемая центром масс, которая обладает рядом интересных и важных свойств. Ее положение относительно начала данной системы координат характеризуется радиус-вектором , определяемым как

,

(2.10)

где – масса и радиус-вектор -й частицы, – масса всей системы, – полное число частиц в системе. Если взять производную по времени от обеих частей уравнения и умножить обе части на , то получится:

или

,

где – скорость движения центра масс системы. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость ее центра масс:

.

Подставив это выражение в (2.9), получим:

.

(2.11)

Отсюда следует, что центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы. Этот результат называется теоремой о движении центра масс системы материальных точек. Уравнение (2.11) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на систему материальных точек: ускорение системы как целого прямо пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы.

Если система замкнута, то 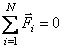и уравнение (2.11) переходит в , следовательно, . Таким образом, центр масс замкнутой системы движется прямолинейно и равномерно или покоится.

Примеры

В безвоздушном пространстве снаряд, выпущенный из пушки под некоторым углом к горизонту, будет двигаться по параболе под действием силы тяжести. Если в какой-либо момент времени снаряд разорвется на мелкие осколки, то эти осколки под действием внутренних сил будут разлетаться в разные стороны. Однако центр масс осколков и газов, образовавшихся при взрыве, будет продолжать свое движение по параболической траектории, как если бы никакого взрыва не было. Действительно, результирующая внешняя сила, действующая на продукты распада, равна силе тяжести, действовавшей на неразорвавшийся снаряд.

 

При взрыве праздничной ракеты центр масс продуктов распада в течение некоторого времени продолжает двигаться по траектории, по которой двигалась бы ракета, если бы взрыва не произошло

2.9. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ.
ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ

 

«Открытие спутников Юпитера, фаз Венеры, солнечных пятен и т.д. потребовало лишь наличие телескопа и некоторого трудолюбия, но нужен был необыкновенный гений, чтобы открыть закон природы в таких явлениях, которые всегда пребывали перед глазами, но объяснение которых, тем не менее, всегда ускользало от изысканий философов». Ж.Л. Лагранж

 

 

 

Галилео Галилей (Galileo Galilei), 1564–1642

Галилео Галилей – великий итальянский физик, механик и астроном. Родился в Пизе в 1564 г. в тот самый день, когда умер Микеланджело. Галилей по праву считается одним из основоположников точного естествознания. Ряд открытий Галилея и некоторые его взгляды имели непосредственное отношение к движению небесных тел. В 1632 г. вышла его книга «Диалог о двух главнейших системах мира – Птолемеевой и Коперниковой», в которой Галилей в доступной форме изложил свои взгляды на систему мира Коперника. А годом позже Галилей был вызван на суд римской инквизиции, и там коленопреклоненный был вынужден поклясться, что отрекается от идеи о неподвижном Солнце и движущейся Земле. Он был взят под домашний арест. Однако Галилей не был сломлен. Страдая от болезней и переживаний, он все же нашел в себе силы и мужество, чтобы написать новую книгу «Беседы и математические доказательства, касающиеся двух новых отраслей наук». Это был самый значительный труд Галилея, в котором сконцентрировались плоды всех его научных поисков. Эта книга была издана в Лейдене в 1636 г.

Заслуга Галилея заключалась в том, что он опроверг ошибочное положение динамики Аристотеля и заложил основы современной механики, выдвинул идею об относительности движения, установил законы инерции, свободного падения и движения тел по наклонной плоскости. Галилей первым направил телескоп в небо, открыл горы на Луне, четыре спутника Юпитера, фазы у Венеры и пятна на Солнце.

Прожив 78 лет, совершенно потеряв зрение, Галилей умер 8 января 1642 г., того самого года, в котором на Земле суждено было появиться Ньютону.

Физики любой эпохи будут с благодарностью и уважением вспоминать Галилея, указавшего на то, что новые идеи надо искать «в великой книге – природе», опираясь только на факты.

В 1632 г. в книге «Диалог о двух главнейших системах мира – Птолемеевой и Коперниковой» Галилей обосновал принцип относительности, ставший одним из первых основных принципов физики. Согласно этому принципу все ИСО по своим механическим свойствам эквивалентны друг другу. Это значит, что никакими механическими опытами, проводимыми внутри данной ИСО, нельзя установить, покоится эта система или движется равномерно и прямолинейно. Этот принцип является обобщением опыта и подтверждается всем многообразием приложений механики Ньютона к движению тел, скорости которых значительно меньше скорости света.

Все сказанное достаточно ясно свидетельствует об исключительности свойств ИСО, в силу чего именно эти системы должны, как правило, использоваться для изучения механических явлений.

Найдем формулы преобразования координат при переходе от одной ИСО к другой. Допустим, что система отсчета S инерциальна. Рассмотрим вторую систему отсчета S', движущуюся относительно первой поступательно с постоянной скоростью 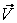(рис. 2.8). Свяжем с каждой системой отсчета декартову систему координат. Пусть известно движение точки в одной из этих систем, например, в системе S, то есть известна зависимость координат точки от времени. Как найти движение той же точки в системе отсчета S'? Задача сводится к нахождению формул, выражающих координаты движущейся точки в системе отсчета S' через ее координаты в системе отсчета S в один и тот же момент времени. Начало координат и направление координатных осей можно выбрать произвольно как в системе отсчета S, так и в системе отсчета S'. Для простоты можно принять, что координатные оси 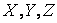системы S соответственно параллельны координатным осям системы S' и что в начальный момент начало системы координат, связанной с системой отсчета S, совпадает с началом системы координат, связанной с системой отсчета S'. Кроме того, предположим, что скорость 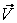параллельна оси 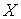. При этих условиях ось будет все время совпадать с осью .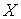

Пусть в момент времени движущаяся точка находится в положении M. За время начало координат S' переходит из точки О в положение 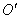, причем, так как то

,

(2.12)

где 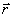и – радиус-векторы движущейся точки соответственно в системах отсчета S и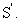

Спроецируем соотношение (2.12) на оси координат:

(2.13)

Формулы обратного преобразования имеют вид

или в координатной форме

(2.14)

Формулы (2.12–2.14) и дают решение поставленной задачи. Они называются преобразованиями Галилея. Мы присоединили к формулам преобразования координат дополнительное выражение , чтобы явно отметить, что время в механике Ньютона считается абсолютным (то есть не меняется при переходе от одной системы отсчета к другой) и поэтому не преобразуется.

С точки зрения «здравого смысла» преобразования Галилея кажутся очевидными. Однако в основе вывода лежит предположение механики Ньютона об абсолютности длин и промежутков времени. Абсолютность времени явно отмечена в уравнении , при выводе остальных формул использовалось предположение об абсолютности длин. Действительно, формулы (2.12–2.14) были бы очевидными, есл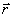и и измерялись бы в одной системе отсчета. Мы же измеряем их в разных системах отсчета. По этой причине без предположения об абсолютности расстояний и промежутков времени нельзя обойтись. Релятивистская физика отказалась от такой абсолютности.

Чтобы получить формулы сложения скоростей в нерелятивистской механике, возьмем производную по времени от (2.12):

или

,

(2.15)

где – скорость точки в системе отсчета S, а – в системе отсчета 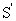. Эта формула выражает закон сложения скоростей в классической механике.

Возьмем производную по времени от (2.15), тогда получим

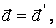
(2.16)

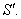где – ускорение точки в системе отсчета S, – в системе отсчета Таким образом, ускорение точки в обеих системах отсчета одинаково. Говорят, что ускорение инвариантно относительно преобразований Галилея.

По определению ИСО свободная материальная точка движется в системе отсчета S без ускорения. Формула (2.16) показывает, что движение данной материальной точки в системе отсчета 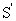будет также неускоренным. Следовательно, 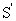– также инерциальная система отсчета. Таким образом, система отсчета, движущаяся относительно инерциальной системы отсчета прямолинейно и равномерно, также является инерциальной системой. Следовательно, если существует хотя бы одна ИСО, то существует и бесконечное множество ИСО, движущихся относительно друг друга равномерно и прямолинейно.

Сила в классической механике может зависеть от разностей координат, разностей скоростей взаимодействующих точек и от времени. Поэтому, как видно из преобразований Галилея, она не меняется при переходе от одной системы отсчета к другой. Отсюда следует, что уравнение, выражающее второй закон Ньютона, остается неизменным при переходе от одной ИСО к другой. Такие уравнения называются инвариантными. Таким образом, уравнения механики Ньютона инвариантны относительно преобразований Галилея. Это утверждение и составляет содержание принципа относительности Галилея. Равноправие ИСО дает возможность в каждом конкретном случае подбирать систему отсчета, наиболее удобную для решения рассматриваемой задачи.

Итак, принцип относительности Галилея выражает полное равноправие всех ИСО. Однако означает ли это, что одно и то же движение выглядит одинаково во всех ИСО? Конечно, нет! Движение тела, свалившегося с полки равномерно движущегося вагона, является прямолинейным, если его рассматривать относительно вагона. Но то же самое движение происходит по параболе в системе отсчета, связанной с полотном железной дороги, хотя законы механики Ньютона одинаковы в обеих системах отсчета. Движения выглядят по-разному, так как для описания движения к уравнению движения необходимо добавить начальные условия, то есть задать начальное положение тела и его начальную скорость, а они будут различными в разных системах отсчета.

РАБОТА И ЭНЕРГИЯ

Зная законы действия сил на систему частиц и состояние системы частиц (координаты и скорости всех частиц) в некоторый начальный момент времени, можно с помощью уравнений движения предсказать ее дальнейшее поведение, то есть найти состояние системы в любой момент времени. Однако детальное рассмотрение поведения системы с помощью уравнений движения часто бывает связано с большими математическими трудностями. А в тех случаях, когда законы действия сил неизвестны, такой подход оказывается в принципе неосуществимым. Поэтому возникает вопрос: нет ли каких-либо общих принципов, которые позволили бы иначе подойти к решению задачи?

Оказывается, такие принципы есть. Это законы сохранения. Законы сохранения позволяют рассмотреть общие свойства движения без решения уравнений движения и подробной информации о развитии процессов во времени. Законы сохранения были установлены опытным путем, как обобщение огромного количества экспериментальных фактов. В механике имеют значение три закона сохранения: закон сохранения энергии, закон сохранения импульса, закон сохранения момента импульса. Эти законы относятся к числу тех фундаментальных принципов физики, значение которых трудно переоценить. Их роль особенно возросла после того, как выяснилось, что они далеко выходят за рамки механики и представляют собой универсальные законы природы. Во всяком случае, до сих пор не обнаружено ни одного явления, где бы эти законы нарушались.

Открыв возможность другого подхода к рассмотрению различных механических явлений, законы сохранения стали мощным и эффективным инструментом исследования, которым повседневно пользуются физики. Эта важнейшая роль законов сохранения как инструмента исследования обусловлена следующими причинами.

Законы сохранения не зависят ни от траекторий движения, ни от характера действующих сил. Поэтому они позволяют получить ряд общих и существенных заключений о свойствах различных механических процессов, не вникая в детальное рассмотрение их с помощью уравнений движения.

Так как законы сохранения не зависят от характера действующих сил, то их можно использовать даже тогда, когда силы неизвестны. В этих случаях законы сохранения являются единственным и незаменимым инструментом исследования.

Даже в тех случаях, когда силы в точности известны, законы сохранения следует использовать при решении многих задач о движении частиц. Хотя все эти задачи могут быть решены с помощью уравнений движения, привлечение законов сохранения очень часто позволяет получить решение наиболее простым путем, избавляя нас от утомительных математических расчетов. Поэтому при решении новых задач обычно принято придерживаться следующего порядка: прежде всего, применяют законы сохранения, и только убедившись, что этого недостаточно, привлекают для решения задачи уравнения движения.