 |
Главная |
Характерные скорости молекул газа
|
из
5.00
|
Наиболее вероятная  (9)
(9)
Средняя  (10)
(10)
Среднеквадратичная  (11)
(11)
Распределение Больцмана
в поле потенциальных сил  (12)
(12)
где 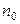 - плотность молекул в том месте, где их потенциальная энергия равна нулю
- плотность молекул в том месте, где их потенциальная энергия равна нулю
Распределение Больцмана
в поле сил тяготения  (13)
(13)
где 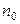 - концентрация молекул на высоте
- концентрация молекул на высоте  .
.
Классическое распределение Максвелла – Больцмана:
 (14)
(14)
где 
Распределение Ферми – Дирака 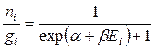 (15)
(15)
Распределение Бозе - Эйнштейна:  (16)
(16)
где 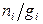 - число частиц, приходящихся на одно состояние с энергией
- число частиц, приходящихся на одно состояние с энергией  ,
, 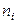 -число неразличимых частиц в
-число неразличимых частиц в 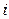 -м состоянии,
-м состоянии,  - число ячеек, по которым могут быть распределены частицы в состоянии с энергией
- число ячеек, по которым могут быть распределены частицы в состоянии с энергией  ,
,  - параметр, зависящий от вида
- параметр, зависящий от вида  и определяемый из условия сохранения числа частиц,
и определяемый из условия сохранения числа частиц,  .
.
Статистический смысл энтропии (определение)  (17)
(17)
Свойство аддитивности энтропии  (18)
(18)
Закон возрастания энтропии  (19)
(19)
Связь изменения энтропии с количеством переданного тепла:
для обратимого процесса  (20)
(20)
для необратимого процесса 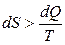 (21)
(21)
Теорема Нернста  (22)
(22)
Варианты тестов промежуточного контроля по теме
ТЕСТ№1
1. В чем состоит статистический подход в молекулярной физике?
2. Состояние, которое характеризует систему в общем и описывается такими параметрами как давление, температура и объем называется _________.
3. Почему силы отталкивания между молекулами убывают быстрее, чем силы притяжения?
4. Сформулируйте третье положение МКТ.
5. Чему равна средняя кинетическая энергия молекулы?
6. Какие параметры связывает основное уравнение МКТ?
7. Приведите соотношение, описывающее распределение молекул по скоростям.
8. Какие скорости называют характерными для распределения Максвелла?
9. Число различных микросостояний, соответствующих данному макросостоянию называют ________.
10. Запишите формулу, выражающее статистическое определение (смысл) энтропии.
ТЕСТ№2
1. Какое состояние называют микроскопическим?
2. Сформулируйте первое положение МКТ.
3. Приведите формулу, связывающую давление газа со среднеквадратичной скоростью его молекул.
4. Наиболее вероятная скорость молекул соответствует ______ и рассчитывается _________.
5. Из формы распределения Максвелла видно, что с ростом температуры характерные скорости молекул _____, а высота кривой в максимуме______.
6. Наиболее вероятная скорость определяется по формуле _______.
7. Средняя скорость находится из соотношения _______.
8. В каком состоянии системы статистический вес является максимальным?
9. Запишите соотношение для распределения Больцмана.
10. Приведите формулу, которая соответствует свойству аддитивности энтропии.
ТЕСТ№3
1. Состояние, которое характеризует положение и скорость каждой частицы системы называется ______.
2. В чем суть второго положения МКТ.
3. На основании какого подхода в молекулярной физике Клаузиус установил зависимость давления от средней кинетической энергии газа?
4. Приведите соотношение, связывающее давление и среднеквадратичную скорость.
5. При каком условии квантовые статистики сводятся к классической?
6. Приведите распределение Больцмана для произвольного поля потенциальных сил.
7. Чему равна средняя скорость в соответствии с распределением Максвелла?
8. Сформулируйте два основных свойства энтропии.
9. Что происходит с энтропией при стремлении температуры к абсолютному нулю?
10. Какой должен быть спин у частиц, подчиняющихся статистике Ферми - Дирака?
ТЕСТ№4
1. Какое состояние называется макроскопическим?
2. Как связана скорость хаотического движения молекул с температурой?
3. Соотношение между среднеквадратичной скоростью молекул и давлением показывает, что чем больше кинетическая энергия молекул газа, тем _______.
4. Приведите функцию распределения Максвелла по кинетическим энергиям.
5. Как найти наиболее вероятную скорость с помощью функции распределения Максвелла?
6. Какой вид имеет функция распределения Больцмана в поле сил тяготения?
7. Что такое энтропия?
8. При абсолютном нуле тело находится в основном состоянии, статистический вес которого _______.
9. В чем выражается свойство аддитивности энтропии?
10. Какой должен быть спин у частиц, подчиняющихся статистике Бозе – Эйнштейна?
|
из
5.00
|
Обсуждение в статье: Характерные скорости молекул газа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

