ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ

 

Теоретический материал

Среднее число соударений, испытываемых одной молекулой газа в единицу времени

,

где d – эффективный диаметр молекул, n – концентрация молекул, - средняя арифметическая скорость молекул.

Средняя длина свободного пробега молекул газа

.

Уравнение диффузии

,

где 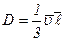- коэффициент диффузии, - градиент плотности в направлении перпендикулярном к площадке, - масса газа, перенесенная в результате диффузии через площадку S, перпендикулярную оси x, за время .

Уравнение теплопроводности

,

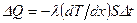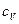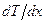где - коэффициент теплопроводности, - удельная теплоемкость газа при постоянном объеме, - плотность газа, - градиент температуры, - количество теплоты, перенесенное газом в результате теплопроводности через площадку S, перпендикулярную оси x, за время .

Сила внутреннего трения, действующая между слоями газа

,

где - коэффициент внутреннего трения, - градиент скорости в направлении, перпендикулярном площадке.

 

Основные типы задач и методы их решения

Классификация

1. Определение эффективного диаметра, средней длины свободного пробега и частоты столкновений молекул.

Метод решения. 1) Использование соотношения между эффективным диаметром, длиной свободного пробега, частотой столкновений и средней скоростью. 2) Использование формул для коэффициентов переноса.

2. Определение изменения величины коэффициентов переноса и газокинетических характеристик молекул в зависимости от изменения параметров состояния газа.

Метод решения. Использование формул для коэффициентов переноса, соотношений между газокинетическими характеристиками явления столкновений молекул и основного уравнения молекулярно-кинетической теории газов.

3. Определение неизвестных характеристик процессов переноса для данного конкретного процесса.

Метод решения. Использование соответствующих уравнений переноса и формул для коэффициентов переноса.

Примеры

Задача 1. Найти среднюю длину свободного пробега и частоту столкновений молекул воздуха при нормальных условиях. Эффективный диаметр молекулы воздуха d = 3×10^-10м, масса одного киломоля M = 29 кг/кмоль.

Решение

Средняя длина свободного пробега молекул газа

.

Учитывая, что , получаем

.

Частота столкновений молекул воздуха, т.е. среднее число соударений, испытываемых одной молекулой в единицу времени, определится по формуле

,

где

.

Подставляя числовые значения в выражения, найдем

м, =4,7×10⁹.

Задача 2. Коэффициент вязкости углекислого газа при нормальных условиях равен 1,4×10^-5 кг/мс. Вычислить длину свободного пробега и коэффициент диффузии молекул СО₂ при нормальных условиях.

Решение

Коэффициент внутреннего трения (вязкости) газа определяется по формуле

,

откуда .

Средняя арифметическая скорость и плотность молекул углекислого газа при нормальных условиях определяется по формулам

, ,

где T₀ = 273 К, p₀ = 1,0×10⁵ Па, M = 44 кг/кмоль.

Проведя расчеты по данным формулам, найдем

r = 1,94 кг/м; м/c, = 5,9×10^{-8 м.}

Из сопоставления выражения для коэффициентов диффузии и внутреннего трения следует

,

откуда, с учетом выражения для плотности,

.

После подстановки числовых значений, получим

7,21×10^-6 м²/c.

 

Задача 3. Как изменится вязкость двухатомного газа при уменьшении объема в два раза, если процесс перехода был: а) изотермическим, б) изобарическим, в) адиабатическим:

Решение

Коэффициент внутреннего трения (вязкости) газа определяется формулой

,

в которую в явном виде не входит объем. Следовательно, необходимо установить зависимость от объема каждого из сомножителей.

Средняя длина свободного пробега молекул

с учетом , прямо пропорциональна объему . С другой стороны, величина обратно пропорциональна объему.

Следовательно, h может зависеть от объема только через среднюю скорость. Для изотермического процесса (Т = const)

,

и, таким образом, h = const.

Для изобарического процесса

.

Следовательно, h 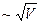, т.е. с уменьшением объема в 2 раза при изобарическом процессе, вязкость уменьшится в раз.

Для адиабатического процесса

и, с учетом этого

,

где 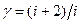=1,4 (i = 5).

Таким образом, .

 

Задача 4. Пространство между двумя большими параллельными пластинами заполнено гелием. Расстояние между пластинами L = 50 мм. Одна пластина поддерживается при температуре Т₁ = 290 К, другая – при Т₂ = 330 К. Давление газа близко к нормальному. Найти плотность потока тепла.

Решение

Так как температуры пластин поддерживаются постоянными, то в пространстве между ними установится постоянное распределение температур. Плотность потока тепла не будет зависеть от времени и определится из уравнения теплопроводности

.

Коэффициент теплопроводности выражается формулой

,

в которой , , ; .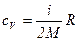

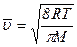С учетом данных соотношений, получим

,

где .

Таким образом, для плотности потока тепла имеем уравнение

.

Разделяя переменные и интегрируя, получим

,

.

Окончательно

.