Формализация примера и основные соотношения (математическая модель)

Линейное программирование

Построение моделей задач линейного программирования

Математическое программирование («планирование»)— это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи (РЗ) возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

Линейное программирование (ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие:

1) показатель оптимальности (целевая функция) L(X) представляет собой линейную функцию от элементов решения ;

2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.

Общая форма записи модели задачи ЛП

Целевая функция (ЦФ) , при ограничениях

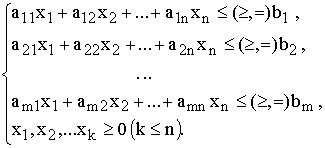
((1.1)

Допустимое решение— это совокупность чисел (план) , удовлетворяющих ограничениям задачи (1.1).

Оптимальное решение —это план, при котором ЦФ принимает свое максимальное (минимальное) значение.

Решение задачи ЛП при помощи надстройки «Поиск решения» в MS Excel

Пример: Оптимальный план выпуска продукции мебельного цеха

Цех может выпускать два вида продукции: шкафы и тумбы для телевизора. На каждый шкаф расходуется 3,5 м стандартных ДСП, 1 м лицевого стекла и 1 человеко-день трудозатрат. На тумбу -1м ДСП, 2 м стекла и 1 человеко-день трудозатрат. Прибыль от продажи 1 шкафа составляет 200 у. е., а 1 тумбы -100 у е. Материальные и трудовые ресурсы ограниченны: в цехе работают 150 рабочих, в день нельзя израсходовать больше 350 м ДСП и более 240 м стекла. Какое количество шкафов и тумб должен выпускать цех, чтобы сделать прибыль максимальной?

 

Формализация примера и основные соотношения (математическая модель)

 

Сведем все данные в следующую таблицу

Таблица 1 – Параметры задачи

Ресурсы	Запасы	Продукты
Шкаф	Тумба
ДСП		3,5
Стекло
Труд
Прибыль, у.е.

В колонке «Ресурсы» запишем предельный расход ресурсов (ДСП, стекла и труда). В колонках «Шкаф» и «Тумба» (продукция, выпускаемая цехом) запишем расход сырья на единицу продукции. Наконец, на пересечении колонок «Шкаф» и «Тумба»и строки «Прибыль» запишем величины прибыли от продаж 1 шкафа и 1 тумбы.

Определим теперь все элементы математической модели данной ситуации (таблица 2):

- переменные решения;

- целевую функцию;

- ограничения.

В данном случае очевидно, что переменные решения (иначе — неизвестные), от которых зависит целевая функция (прибыль) цеха, — это количество шкафов и тумб, выпускаемых цехом. Обозначим эти переменные соответственно x₁ и х₂.

Таблица 2 – Элементы модели

Переменные решения	Целевая функция
x1 — количество шкафов х2 — количество тумб, производимых цехом	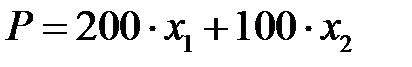прибыль цеха
Ограничения

 

Нетрудно также понять, как в данном случае записывается выражение для целевой функции.

Прибыль от продажи одного шкафа равна 200 у. е., значит, прибыль от продажи x₁ шкафов будет 6∙x₁. Аналогично прибыль от продажи x₂ тумб равна 5∙x₂, что и отражено в соответствующей графе таблицы. Глядя на выражение для целевой функции (типичное для моделей линейного программирования), можно легко увидеть, что, чем больше будут значения переменных x₁ и x₂, тем больше будет и прибыль Р. Если бы было возможно беспредельно увеличивать ежедневный выпуск шкафов и тумб, прибыль росла бы беспредельно. Ясно, однако, что это невозможно, поскольку доступные запасы ресурсов ограничены. Это приводит к ограничениям на значения переменных x₁ и x₂.

Займемся теперь этими ограничениями. Запишем неравенство, отражающее ограниченность запасов шкафов. Поскольку на 1 шкаф расходуется 3,5 м ДСП, а на 1 тумбу — 1 м, то суммарный расход ДСП на x₁ шкафов и x₂ тумб будет, очевидно, 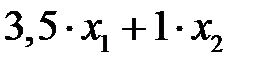, что не должно превышать запаса ДСП в цехе, т.е. 350 м ДСП. Это отражено первым неравенством, записанным в таблице 2. Точно так же получаются второе и третье неравенства, отражающие ограниченность запасов стекла и человеко-день трудозатрат. Естественно, переменные решения не могут быть отрицательными числами, что отражено в последнем ограничении в таблице 2.

Определение переменных решения, целевой функции и ограничений — это почти все, что должен сделать менеджер, чтобы воспользоваться результатами оптимизации и анализа линейной модели. Далее необходимо только правильно организовать данные для компьютера, а все остальное сделает компьютерный алгоритм оптимизации.

 

2.2 Решение задачи об оптимальном плане выпуска продукции с помощью Excel

 

1. Организуйте данные на листе MS Excel так, как это показано на рисунке 1.

a) В ячейку G9 введена целевая функция , представляющая собой прибыль от продажи x₁ десятков свитеров и x₂ десятков кофточек.

b) В ячейки G6, G7, G8 — формулы, отражающие расход сырья при изготовлении x₁ десятков свитеров и x₂ десятков кофточек.

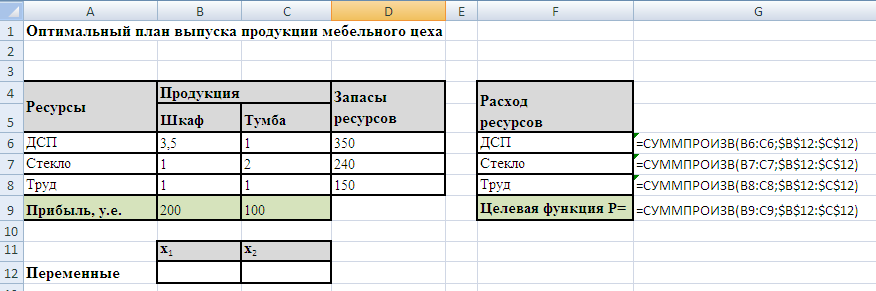
Рисунок 1 – Организация данных на листе MS Excel для примера «Оптимальный план производства трикотажной фабрики»

 

2. Выберите вкладку «Данные» à «Поиск решения». Появится окно, озаглавленное «Поиск решения»(рисунок 2).

а) В поле окна «Установить целевую ячейку» отметьте ячейку G9 (щелкните сначала по полю окна, а затем по ячейке G9);

b) Установите переключатель на отметке «Равной максимальному значению»;

c) В поле окна «Изменяя ячейки» отметьте ячейки В12:С12.

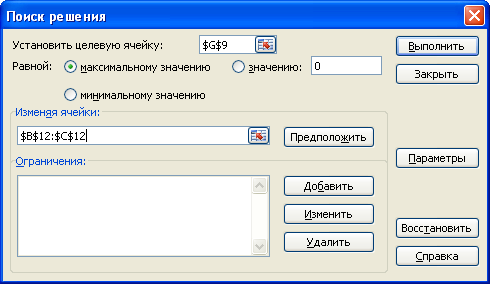
Рисунок 2 – Общий вид и работа с окном «Поиск решения»

 

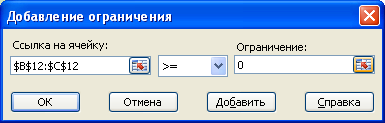
Добавьте ограничения, щелкая по кнопке «Добавить». В появившемся окне, озаглавленном «Добавление ограничения» (рисунок 3), щелкните по полю «Ссылка на ячейку», а затем отметьте ячейки В12:С12, выберите знак ограничения, щелкните по правому полю «Ограничение» и введите в него значение 0. Таким образом, вы ввели ограничение 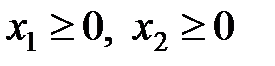. Вновь щелкните по кнопке «Добавить».

.

Рисунок 3 – Общий вид и работа с окном «Добавление ограничения»

 

e) В появившемся окне «Добавление ограничения» щелкните в поле «Ссылка на ячейку», а затем отметьте ячейку G6, выберите знак ограничения (≤), щелкните по правому полю «Ограничение» и отметьте в нем ячейку D6, содержащую ограничение на ресурс «ДСП». Таким образом, вы ввели ограничение ;

f) Продолжайте процесс, пока не введете остальные два ограничения.

3. Щелкните по кнопке «Параметры». Появится окно «Параметры поиска решения» (рисунок 4), в котором можно (но не нужно) менять многочисленные параметры оптимизации. Вас интересует только, установлен ли флажок «Линейная модель». Если нет, установите его, щелкните по кнопке Ok и вернитесь к окну «Поиск решения».

Рисунок 4 – «Параметры поиска решения» в MS Excel

 

Установка параметров оптимизации в окне «Поиск решения»должна выглядеть так, как показано на рисунке 5.

Рисунок 5 – Ввод данных для примера «Оптимальный план выпуска продукции мебельного цеха» в окно «Поиск решения»

 

Замечание

а) Первое ограничение ( 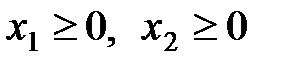) можно не добавлять в список ограничений в окне «Поиск решения», вместо этого можно поставить флажок «Неотрицательные значения» в окне «Параметры поиска решения»;

b) Если ограничения имеют один и тот же знак и расположены на листе MS Excel в смежных ячейках (и если запасы ресурсов также расположены в смежных ячейках), то в окне «Добавление ограничения» в полях «Ссылка на ячейку»и «Ограничение»можно указывать не отдельные ячейки, а диапазоны ячеек (рисунок 6).

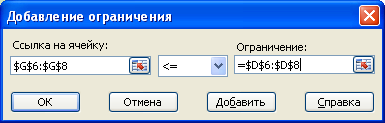
Рисунок 6 – Пример ввода ограничений в окно «Добавление ограничения»

 

4. Щелкните по кнопке «Выполнить». Оптимизационная программа MS Excel выполнит поиск решения, после чего появится окно «Результаты поиска решения» (рисунок 7). Прочтите сообщение программы в этом окне. Если вы все сделали правильно, программа сообщит: «Решение найдено. Все ограничения и условия оптимальности выполнены».

 

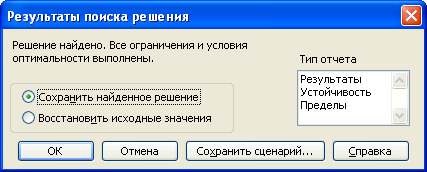
Рисунок 7 – Вид окна «Результаты поиска решения»

Вид листа MS Excel, соответствующий оптимальному решению, показан на рисунке 8.

Рисунок 8 – Вид листа MS Excel, соответствующий оптимальному решению

 

В этом случае убедитесь, что переключатель в окне «Результаты поиска решения» находится в положении «Сохранить найденное решение», щелкните по кнопке Ok и прочтите ответ в ячейках В12:С12. В ячейках G6:G8 содержатся значения ресурсов, которые необходимы для полученного оптимального плана. В случае, если вы неверно задали знак ограничений, ввели неверные формулы для целевой функции или для ограничений и оптимизационная программа не может найти решения, в окне появятся сообщения «Значения целевой ячейки не сходятся»или «Поиск не может найти решения», или «Условия линейной модели не выполняются». В этом случае следует переставить переключатель в окне «Результаты поиска решения»в положение «Восстановить исходные данные», щелкнуть по кнопке Ok и проверить организацию данных на листе Excel и в установках окна «Поиск решения».