Тема 5.2. Элементы теории оценок и проверки гипотез

1. Заданы математическое ожидание т исреднее квадратическое отклонение σнормально распределенной случайной величины х. Найти: 1) вероятность того, что х примет значение, принадлежащее интервалу (α, β); 2) вероятность того, что абсолютная величина отклонения \х—т\ окажется меньше δ.

1.1. т=15, σ=2, α=16, β=25, δ=4.

1.2. т=14, σ=4, α=18, β=34, δ=8.

1.3. т=13, σ=4, α=156, β=17, δ=6.

1.4. т=12, σ=5, α=17, β=22, δ=15.

1.5. т=11, σ=3, α=17, β=26, δ=12.

1.6. т=10, σ=2, α=11, β=13, δ=5.

1.7. т=9, σ=4, α=15, β=19, δ=18.

1.8. т=8, σ=2, α=6, β=15, δ=8.

1.9. т=7, σ=5, α=2, β=22, δ=20.

1.10. т=6, σ=3, α=0, β=9, δ=9.

2. Найти выборочное уравнение прямой 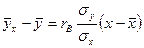регрессии У на Х по данной корреляционной таблице.

 

2.1.

У	Х	пу
			-	-	-	-
	-	-		-	-
	-					-
	-	-				-
		-	-	-
пх							п=100

 

2.2.

У	Х	пу
	-	-			-	-
	-		-	-	-
		-		-		-
	-				-	-
		-	-		-
пх							п=100

 

2.3.

У	Х	пу
	-	-	-			-
	-			-	-	-
	-		-			-
	-	-			-
		-	-			-
пх							п=100

 

2.4.

У	Х	пу
	-	-	-	-		-
	-			-	-	-
		-				-
	-					-
	-	-	-		-
пх							п=100

 

2.5.

У	Х	пу
		-	-	-	-
	-			-	-	-
	-	-				-
	-					-
			-	-		-
пх							п=100

 

2. В задаче выборочные совокупности заданы из соответствующих генеральных совокупностей. Требуется: 1) по несгруппированным данным найти выборочную среднюю; 2) найти доверительный интервал для оценки неизвестного математического ожидания признака X генеральной совокупности (генеральной средней), если признак X распределен по нормальному закону; известно g -надежность и s - среднее квадратическое отклонение; 3) составить интервальное распределение выборки с шагом h, взяв за начало первого интервала х₀; 4) построить гистограмму частот; 5) дать экономическую интерпретацию полученных результатов.

 

3.1 Получены результаты о фондовооруженности в 25 производственных объединениях (тыс. руб.):

16,8 17,2 17,6 17,6 17,9 18,0 18,2 18,4 18,6 18,9 18,9

19.0 19,1 19,2 19,2 19,3 19,7 19,9 20,0 20,0 20,2 20,3

20,4 20,8 21,5

g=0,95; s=1; h=1; х₀=16,5.

 

3.2. Для определения удельного веса активных элементов основных производственных фондов было выборочно обследовано 25 производственных объединений и получены следующие результаты:

22,3 23,7 24,5 25,9 26,1 26,6 27,3 27,9 28,2 28,5 28,8

29.1 29,2 29,9 30,5 30,7 31,4 32,2 32,3 33,5 34,2 34,4

34.9 35,7 38,9

g=0,95; s=4; h=5; x₀=20.

 

3.3. Произведено выборочное обследование 25 магазинов по величине товарооборота. Получены следующие результаты (в тыс. руб.):

42,5 60,0 63,5 70,5 82,0 83,5 92,0 95,5 100,0 101,0 105,0

108,5 110,0 115,5 120,0 120,5 122,0 130,0 138,5 140,0

142,0 150,5 160,0 162,1 180,5

g=0,96; s=31; h=20; х₀=42,5.

 

3.4. При изучении уровня инфляции за некоторый период времени было обследовано 25 стран, получены следующие результаты:

0,35 0,41 0,53 0,59 0,64 0,68 0,71 0,73 0,77 0,78 0,82

0,83 0,85 0,86 0,88 0,89 0,92 0,93 0,97 1,01 107 108 1,14 1,25 1,28

g=0,98; s=0,22; h=0,2; х₀=0,3.

 

3.5. Для определения себестоимости продукции было произведено выборочное обследование 25 предприятий пищевой промышленности и получены следующие результаты (руб.)

15,0 16,4 17,8 18,0 18,4 19,2 19,8 20,2 20,6 20,6

20,6 21,3 21,4 21,7 22,0 22,2 22,3 22,7 23,0 24,2

24,2 25,1 25,3 26,0 26,5 27,1.

g=0,95; s=2,8; h=2,5; x₀=15.

 

3.6. Проведено выборочное обследование 25 частных фирм по количеству занятых в них служащих, получены следующие результаты (чел.):

266 278 315 336 347 354 368 369 391 408

411 416 427 437 444 448 457 462 481 483

495 512 518 536 576

g=0,96; s=65; h=50; х₀=250.

 

3.7. Проведена случайная выборка личных заемных счетов в банке, получены следующие результаты (тыс. руб.):

1850 2200 2400 2450 2500 2550 2800 2900 2950 3100

3150 3200 3200 3300 3350 3400 3450 3550 3550 3600

3800 3900 4100 4300 4550

g=0,96; s=690; h=500; x₀=1550.

 

3.8. Выборочно исследовано 25 предприятий для определения объема выпущенной продукции в месяц на одного рабочего, получены следующие результаты:

773 792 815 827 843 854 861 869 877 886 889 892 885

901 903 905 911 918 919 923 929 937 941 955 981

g=0,92; s=50; h=40; x₀=760.

 

3.9. В Сбербанке проведено выборочное обследование 25 вкладов, которое дало следующие результаты (тыс.руб.):

75 210 350 350 400 520 540 560 590 680 700 700 720

750 780 790 810 850 875 890 1000 1000 1100 1200 1250

g=0,95; s=280; h=250; х₀=50.

 

3.10. При исследовании объема продаж некоторого товара в супермаркете за 25 дней были получены следующие результаты (шт.):

69 76 77 79 83 86 87 88 89 89 90 91 91 92 93 93

94 94 96 96 99 101 103 107 108

g=0,98; s=9,5; h=10; х₀=65.

4. Пусть зависимость признака у от х характеризуется таблицей.

 

хi	-3	-2	-1
yi	2,6	-0,3	-2	-2,3	-1,5	0,7	3,2

 

Предполагая, что справедлива зависимость у = а₀ + а₁х + а₂х², определить оценки коэффициентов а_к.

 

5.Применяя способ наименьших квадратов, составить уравнение параболы второго порядка, которая проходит возможно ближе к точкам, указанным в таблице.

хi	-4	-3	-2	-1
yi				0,3	-0,1	-0,2		0,2

 

 

6.Себестоимость у (в рублях) одного экземпляра книги в зависимости от тиража х (тыс. экз.) характеризуется данными, приведенными в таблице.

хi
yi	1,25	1,15	1,00	0,80	0,65	0,41	0,36	0,20	0,15	0,1

 

Применяя способ наименьших квадратов, определить коэффициенты для гиперболической зависимости вида у = а / х + b.

7. В ходе этнографической экспедиции по двум этнокультурным группам (районам) Архангельской области были выявлены наиболее часто встречающиеся узоры русской вышивки: конь и крылатая птица. На основе частоты появления этих образов орнамента в обследуемых этнокультурных группах была составлена следующая таблица:

Район	конь	крылатая птица
Онежский
Плисецкий

По имеющимся данным построить таблицу сопряженности и по ней 1) оценить тесноту связи между признаками; 2) при уровне значимости 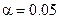проверить нулевую гипотезу о независимости исследуемых признаков: вид орнамента и принадлежность его к определенной группе.

 

8. В ходе медицинского обследования стояла задача проверить аллергенность нового препарата. Из 100 пациентов с одним и тем же заболеванием часть принимала старый общеизвестный препарат X, а часть принимала новый препарат Y. Из принимавших старый препарат: у 48 человек была нормальная реакция, а у 4 человек обнаружена аллергия. Среди тех, кто принимал новый препарат: у 42 зафиксирована нормальная реакция,. А у 6 человек аллергия. Проверить гипотезу о равенстве вероятностей возникновения аллергии при применении препаратов X и Y, когда уровень значимости равен 0,02. останется ли принятое решение о проверке данных гипотез справедливым, если при тех же значения частостей число пациентов возрастет в 10 раз?

 

9. На заводе изготовлен новый игровой автомат, который должен обеспечить появление выигрыша в одном случае из 100 бросаний монеты. Для проверки годности автомата произведено 400 испытаний, где выигрыш появился 5 раз. Оценить вероятность появления выигрыша. Построить приближенные доверительные границы для этой вероятности при , используя: преобразование арксинуса. Как изменится доверительный интервал, если при той же частости появления выигрыша число наблюдений возрастет в 20 раз?

 

10. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	-1	3
Y	2	3	1	4

Предполагая, что между X и Y имеется зависимость вида найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

 

11. Пусть вероятность того, что покупателю магазина женской обуви необходимы туфли 37 размера, равна 0,25. Оценить с помощью теоремы Бернулли и интегральной теоремы Муавра-Лапласа, вероятность того, что доля покупателей, которым необходимы туфли 37 размера, отклонится по абсолютной величине от вероятности 0,25 не более чем на 0,1, если всего в день магазин посещает 1000 покупателей.

 

12. Из 250 абитуриентов, сдававших вступительный экзамен по математике, в одном потоке 63 человека получило неудовлетворительные оценки. Оценить вероятность получения неудовлетворительной оценки на экзамене. Используя интегральную теорему Лапласа построить доверительные границы для этой вероятности при . Как изменится этот интервал, если при той же частости, число абитуриентов возрастет в 10 раз?

 

13. Из проконтролированных 100 телевизоров, выпущенных на Воронежском заводе, целиком удовлетворяют заданным техническим требованиям 85. При контроле 105 телевизоров, выпущенных на Шауляйском заводе, заданным техническим требованиям удовлетворяет 98 телевизоров. Проверить гипотезу о равенстве вероятностей выпуска годного телевизора на этих заводах при уровне значимости 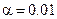. Останется ли принятое решение в силе, если при тех же значениях частостей число проконтролированных телевизоров возрастет в 20 раз?

 

14. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	4	6
Y	2	2,5	2,3	2,1

Предполагая, что между X и Y имеется зависимость вида 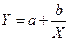найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

 

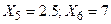15. Из 450 деталей, изготовленных станком-автоматом оказалось 39 нестандартных. Оценить вероятность того, что произвольным образом взятая деталь окажется стандартной. Используя преобразование арксинуса, построить приближенные доверительные границы для этой вероятности при . Как изменится доверительный интервал, если при той же частости изготовления стандартных деталей число наблюдений возрастет в 25 раз?

 

16. В ходе социологических исследований, Стояла задача выявить, зависят ли миграционные установки выпускников от того, в каком регионе они живут. Результаты опроса представлены в таблице:

 

Город	Навсегда уехать	Жить в своем городе постоянно
Пермь
Екатеринбург

По имеющимся данным построить таблицу сопряженности и по ней 1) оценить тесноту связи между признаками; 2) при уровне значимости 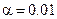проверить нулевую гипотезу о независимости исследуемых признаков: место жительства респондента и его миграционная установка. Изменится ли принятое решение, если все данные увеличить в 40 раз?

 

17. Пусть вероятность того, что автомат по продаже горячих напитков сработает равна 0,97. Пользуясь теоремой Бернулли, оценить вероятность того, что при использовании 1000 наборов из купюр в автомате отклонение частости правильной работы автомата от ее вероятности не превысит по абсолютной величине 0,02.

18. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	0	1	5	6
Y	5	3	4	7

Предполагая, что между X и Y имеется зависимость вида найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

Раздел 6. Случайные процессы