Форма отчета к практической работе № 1

Практическая работа № 1

 

Тема: Приготовление раствора заданной концентрации.

 

Цель работы: Отработать навыки решения расчетных задач.

 

Теоретическая часть

 

Правило смешения или «конверт Пирсона».

 

При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешении. При расчетах записывают одну над другой массовые доли растворенного вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.

 

ЗАДАЧА 1

 

Определите концентрацию раствора, полученного при слиянии 150 г 30%-го и 250 г 10%-го растворов какой-либо соли.

Дано:

m1 = 150 г,

m2 = 250 г,

W1 = 30%,

W2 = 10%.

Найти: W3.

 

Решение:

1-й способ (метод пропорций).

Общая масса раствора:

 

m3 = m1 + m2 = 150 + 250 = 400 г.

 

Массу вещества в первом растворе находим методом пропорций, исходя из определения: процентная концентрация раствора показывает, сколько граммов растворенного вещества находится в 100 г раствора:

 

100 г 30%-го р-ра – 30 г в-ва,

150 г 30%-го р-ра – х г в-ва,

х = 150•30/100 = 45 г.

 

Для второго раствора составляем аналогичную пропорцию:

 

100 г 10%-го р-ра – 10 г в-ва,

250 г 10%-го р-ра – y г в-ва,

y = 250•10/100 = 25 г.

Следовательно, 400 г нового раствора содержит 45 + 25 = 70 г растворенного вещества.

Теперь можно определить концентрацию нового раствора:

 

400 г р-ра – 70 г в-ва,

100 г р-ра – z г в-ва,

z = 100•70/400 = 17,5 г, или 17,5%.

 

2-й способ (алгебраический).

 

m1•W1 + m2•W2 = W3(m1 + m2). Отсюда

W3 = (m1•W1 + m2•W2)/(m1 + m2). В результате находим:

W3 = (150•30 + 250•10)/(150 + 250) = 17,5%.

 

3-й способ (правило креста).

 

 

(W3 – 10)/(30 – W3) = 150/250. Тогда

(30 – W3)•150 = (W3 – 10)•250,

4500 – 150W3 = 250W3 – 2500,

4500 – 2500 = 250W3 – 150W3,

7000 = 400W3

3 = 7000/400 = 17,5%.

 

Ответ. При слиянии взятых растворов получится новый раствор с концентрацией W3 = 17,5%.

 

ЗАДАЧА 2

Определите, сколько нужно взять 10%-го раствора соли и 30%-го раствора этой же соли для приготовления 500 г 20%-го раствора.

Дано:

W1 = 10%,

W2 = 30%,

W3 = 20%,

m3 = 500 г.

Найти: m1, m2.

 

Решение

 

Используем правило креста.

 

Для приготовления 500 г 20%-го раствора соли нужно взять по 10 частей растворов исходных концентраций.

Проверим правильность нашего решения, учитывая, что 1 часть равна 500/(10 + 10) = 25 250 г 10%-го р-ра – х г соли,

100 г 10%-го р-ра – 10 г соли,

х = 250•10/100 = 25 г.

 

250 г 30%-го р-ра – y г соли,

100 г 30%-го р-ра – 30 г соли,

y = 250•30/100 = 75 г.

 

m(р-ра) = 250 + 250 = 500 г.

m(соли) = 25 + 75 = 100 г. Отсюда находим W3:

 

500 г р-ра – 100 г соли,

100 г р-ра –W3 г соли,

 

W3 = 100•100/500 = 20 г, или 20%.

 

Ответ. Для приготовления 500 г 20%-го раствора нужно взять исходные растворы по 250 г (m1 = 250 г, m2 = 250 г).

 

ЗАДАЧА 3

Определите массу раствора Nа2СО3 10%-й концентрации и массу сухого кристаллогидрата Na2CO3•10H2O, которые нужно взять для приготовления 540 г раствора 15%-й концентрации.

Дано:

W1 = 10%,

W3 = 15%,

m3 = 540 г.

Найти: m1, m2.

 

Решение

 

1-й способ (через систему уравнений с двумя неизвестными).

 

Определяем массу соли Na2CO3 в 540 г 15%-го раствора:

100 г 15%-го р-ра – 15 г соли,

540 г 15%-го р-ра – z г соли,

z = 540•15/100 = 81 г.

 

Cоставляем систему уравнений:

 

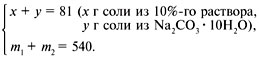
Находим молярную массу:

 

 

Избавляемся от лишних неизвестных: m2 = 286y/106;

 

100 г 10%-го р-ра – 10 г соли,

m1 г 10%-го р-ра – х г соли,

m1 = 100х/10 = 10х.

 

Подставляем m2 и m1 в систему уравнений:

 

 

С учетом того, что х = 81 – y, избавляемся от второго неизвестного:

10(81 – y) + 286y/106 = 540. Отсюда

y = 270/7,3 = 37 г.

 

Тогда m2 = 286y/106 = 2,7•37 100 г – это масса необходимого количества кристаллогидрата Na2СО3•10H2O.

Далее находим: х = 81 – y = 81 – 37 = 44 г – это масса соли из 10%-го раствора.

Находим массу 10%-го раствора:

 

100 г 10%-го р-ра – 10 г соли,

m1 г 10%-го р-ра – 44 г соли,

m1 = 100•44/10 = 440 г.

 

2-й способ (правило креста).

Допустим, что Na2СО3•10H2O – это «сухой раствор» (ведь он же содержит воду). Тогда найдем его «концентрацию»:

 

 

286 г – 106 г соли,

100 г – х г соли,

х = 100•106/286 = 37 г, или 37%.

 

Применяем правило креста.

 

 

Находим массу одной части и массы веществ: 540/27 = 20 г,

 

m1 = 20•22 = 440 г, m2 = 20•5 = 100 г.

 

Ответ. Для приготовления 540 г раствора Na2CO3 15%-й концентрации необходимо взять 440 г 10%-го раствора и 100 г кристаллогидрата.

 

 

Упражнения

 

1.Сколько миллилитров воды надо прилить к 80 г 5 %-ного раствора соли, чтобы получить 2 %-ный раствор?

2.Сколько грамм соли надо добавить к 150 г 0,5 %-ного раствора этой соли, чтобы получить 6 %-ный раствор?

3.Сколько миллилитров воды надо прилить к 200 г 6 %-ного раствора сахара, чтобы получить 1,5 %-ный раствор сахара?

4.Сколько воды надо прилить к 80 г 10 %-ного раствора гидроксида натрия, чтобы получить 3 %-ный раствор?

5.Сколько грамм сахара надо добавить к 300 г 2 %-ного раствора, чтобы получить 5 %-ный раствор?

6.Сколько миллилитров воды надо добавить к 70 г 20 %-ного раствора серной кислоты, чтобы получить 3 %-ный раствор?

7.Сколько воды нужно добавить к 250 г раствора соли для понижения его концентрации с 45% до 10%?

8.Сколько сухой соли нужно добавить к 250 г раствора 10%-й концентрации для ее увеличения до 45%?

 

Форма отчета к практической работе № 1

 

1.Номер практической работы

2.Наименование практической работы

3.Цель

4.Решение задач

5.Список использованных источников