Интегралы от экспоненты, умноженной на многочлен

 

Общее правило: заu всегда обозначается многочлен.

 

Пример 5

Найти неопределенный интеграл.

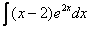
Решение:

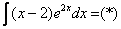
Используя знакомый алгоритм, интегрируем по частям:

Если возникли трудности с интегралом 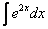, то следует вернуться к статье Метод замены переменной в неопределенном интеграле.

Единственное, что еще можно сделать, это «причесать» ответ:

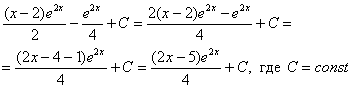
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом ,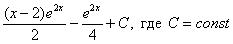

или даже .

То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.

 

Пример 6

Найти неопределенный интеграл

.

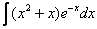Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что 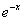– сложная функция.

 

 

Интегралы от тригонометрических функций, умноженных на многочлен

 

Общее правило: заu всегда обозначается многочлен.

Пример 7

Найти неопределенный интеграл.

Интегрируем по частям:

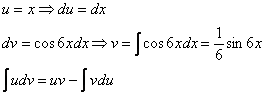
Пример 8

Найти неопределенный интеграл

.

Это пример для самостоятельного решения.

 

Пример 9

Найти неопределенный интеграл

.

Еще один пример с дробью. Как и в двух предыдущих примерах заu обозначается многочлен.

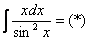
Интегрируем по частям:

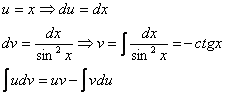
Пример 10

Найти неопределенный интеграл

.

Это пример для самостоятельного решения.

Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.

 

 

Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен

 

Общее правило: за u всегда обозначается обратная тригонометрическая функция.

Напоминаем, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи мы будем называть их «арками».

 

Пример 11

Найти неопределенный интеграл.

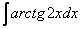
Решаем.

.

Интегрируем по частям:

Здесь интеграл найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример разбирался на уроке Метод замены переменной в неопределенном интеграле.

Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять другие методы и приёмы решения.

 

Пример 12

Найти неопределенный интеграл

.

Это пример для самостоятельного решения.

 

И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков, желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.

 

Пример 13

Найти неопределенный интеграл

.

Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.

 

 

Решения и ответы:

 

Пример 3: Решение:

.

 

Пример 4: Решение:

Интегрируем по частям:

.

 

Пример 6: Решение:

Дважды интегрируем по частям:

 

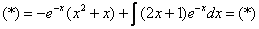
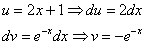
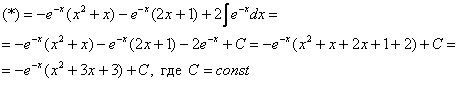
Пример 8: Решение:

Интегрируем по частям:

 

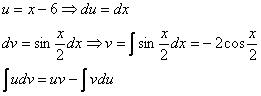
Пример 10: Решение:

Интегрируем по частям:

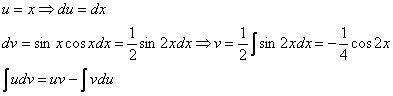
Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла 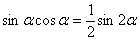. Её можно было использовать и сразу: 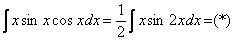, а потом интегрировать по частям.

 

Похожим способом также решаются интегралы вроде 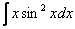, – в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул.

Более подробно – см.Интегралы от тригонометрических функций.

 

Пример 12:

Интегрируем по частям:

 

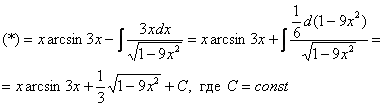
Пример 13:

Интегрируем по частям:

 

Примечание: Если возникли трудности с интегралом

,

то следует посетить урок Интегрирование некоторых дробей.