ЭКОНОМИЧЕСКАЯ ТЕОРИЯ БЛАГОСОСТОЯНИЯ

В экономике достаточно часто стоит вопрос об определении эффективности государственной политики в отношении граждан, жителей данного государства. По сути, речь идет о сопоставлении частных преимуществ индивида при проведении государственного проекта с общественной выгодой данного общества.

При этом у каждого домохозяйства есть четко выверенная иерархия своих предпочтений относительно социальных решений, что подразумевает выполнимость основных аксиом потребительского выбора упорядоченности, транзитивности и рефлексивности. Центральным вопросом теории экономического благосостояния становится вопрос о существовании такого правила агрегирования предпочтений индивидов, которое удовлетворяло бы всех членов общества. Подобного рода вопрос предполагает создание специфических «разумных» правил агрегирования, которые бы позволили связать общественные и индивидуальные предпочтения.

Один из механизмов формирования функции общественного благосостояния – голосование.

Представим себе, что в обществе имеются три группы депутатов, которые должны принять решение в отношении трех законопроектов. Предпочтения каждой группы депутатов представлены в табл. 1.

 

Группа депутатов	Законопроект
	А	В	С

 

Например, для первой группы депутатов наиболее предпочитаемым законопроектом будет А, для второй – В, для третьей – С. На втором месте депутаты первой группы ставят законопроект В, депутаты второй группы – законопроект С, и депутаты третьей группы – законопроект А. И наконец, наименее предпочтительным для первой группы будет законопроект С, для второй группы – законопроект А, для третьей группы – законопроект В.

Предположим, для выявления исхода голосования используется принцип простого большинства голосов. Тогда при голосовании между законопроектами А и В две группы депутатов (первая и третья) проголосуют «за», вторая группа депутатов проголосует «против». При одинаковом числе депутатов в каждой группе законопроект А будет принят большинством голосов. Точно также большинством голосов будет принят законопроект В при выборе между В и С. Так как законопроект А предпочитается большинством голосов законопроекту В, а законопроект В предпочитается большинством голосов законопроекту С, логично было бы ожидать, что законопроект А предпочитается законопроекту С. Однако, как мы видим из таблицы предпочтений, при голосовании между законопроектами А и С большинство голосов (группы вторая и третья) будет отдано за С. Таким образом, механизм голосования по принципу большинства голосов выявляет серьезный недостаток – невозможность последовательного принятия решений, или парадокс голосования, известный как парадокс Кондорсе.

Конечно, принцип принятия решений большинством голосов не обязательно приводит к парадоксу голосования. При других видах предпочтений общества принцип большинства голосов сопровождается последовательностью общественного выбора. Однако этим не исчерпываются все проблемы принятия решений в обществе.

Пусть предпочтения в обществе демонстрируют последовательность, так что парадокса голосования не возникает. Каждая группа депутатов голосует за законопроект, который отражает ее предпочтения или оказывается наиболее близким к ее предпочтениям и соответственно голосует против того законопроекта, который находится дальше всего от ее спектра предпочтений. Другими словами, каждая группа депутатов характеризуется одновершинными предпочтениями[90], которые в целом дают транзитивность предпочтениям общества.

В данном случае общественные решения, принятые большинством голосов, будут отражать предпочтения «среднего избирателя», расположенные в середине возможной шкалы общественных предпочтений. Позиция среднего избирателя всегда будет предпочтительнее любой крайней точки зрения, поскольку за эту позицию будет отдано большинство голосов. Пусть, например, три группы депутатов рассматривают объемы расходов на национальную оборону. И пусть их предпочтения распределяются таким образом (табл. 2):

Таблица 2

Группа депутатов	Объем расходов на национальную оборону, в млрд. руб.

 

Объемы расходов в 100 и 35 млрд. руб. не будут приняты, поскольку за них проголосуют только депутаты соответствующих групп: против объема расходов в 100 млрд. руб. проголосуют депутаты второй и третьей группы; против объема расходов в 35 млрд. руб. проголосуют депутаты первой и второй группы. Объем расходов в 60 млрд. руб. (некая промежуточная величина) будет принят большинством голосов либо второй и первой группами (если первая группа расценит 60 млрд. руб. на оборону лучше, чем «ничего» в виде 35 млрд. руб., предлагаемых третьей группой), либо второй и третьей группами (если третья группа расценит 60 млрд. руб. лучше, чем слишком большая сумма в 100 млрд. руб., предлагаемая первой группой).

Следовательно, последовательность общественного выбора при механизме голосования по принципу большинства голосов будет наблюдаться тем в большей степени, чем в большей степени каждый голосующий рассматривает «второе наилучшее решение» в качестве исхода, близкого к предпочитаемому им самим результату. Данное утверждение носит название теорема Блэка, которая гласит: «Если число голосующих нечетно и все они обладают однопиковыми предпочтениями, то процедура голосования большинством обеспечивает полное и транзитивное упорядочение». Если же голосующие действуют по правилу «все или ничего», велика вероятность непоследовательности общественного выбора и парадокса голосования; нахождение позиции среднего избирателя в данном случае означает бессмысленную трату времени.

Еще один метод решения вопросов – это создание коалиционных групп, так как меньшинство может защитить свои права путем созданий коалиций либо со многими такими же малочисленными партиями, какой является сама, либо путем присоединения к одной большой партии, которой все же не хватает голосов для принятия нужного ей решения. У партий в коалиции могут совпадать взгляды хотя бы по некоторым позициям, в остальных же случаях они делают взаимные уступки в соответствии со своими приоритетами. Последние выборы в Эстонии и в Германии доказали это, поскольку выиграли партии, которые создали коалиции c малочисленными и несущими узкие и специфические идеи (в данном случае это были «зеленые»), близкие, однако, особенно в совокупности c крупными пакетами программ, большей части общества. Кроме того, особенно значимые законы парламентарии по регламенту должны принимать квалифицированным большинством (2/3 голосов), что позволяет учитывать мнение не только той партии, которая обладает простым большинством.

Процесс диктата можно объяснить на примере образования коалиций. Пусть у I лица выбор падает на А, у II – на В, у III – на С. Если голосование производилось бы по принципу простого большинства, то избиратели II и III не смогли бы выбрать А, I и III не смогли бы выбрать В, а I и II – C.

Таблица 3

	Альтернативы	Общее число баллов
A	B	C
Голосующие лица	I
II
III
Общее число баллов

 

В табл. 3 выражена идея о том, что сконцентрированные интересы и предпочтения оказывают более сильное влияние, чем размытые и менее концентрированные. Но поскольку в большинстве случаев существует большая дисперсия (разброс) интересов и предпочтений избирателей, то на практике широкое применение находит метод образования коалиции и обмена голосов (logrolling).

Таблица 4

	Альтернативы	Общее число баллов
A	B	C
Голосующие лица	I
II
III
Общее число баллов

 

Эффективность лоббизма определяется тем, что сплоченная группа, действующая активно и целенаправленно, может добиваться принятия решений, выгодных для меньшинства, если большинство разобщено и индивидуальная предельная выгода каждого члена большинства в отдельности меньше индивидуальных предельных затрат, связанных с ее получением. Для усиления эффективности лоббизма могут применяться такие методы, как рассмотренный выше договор о взаимной поддержке, а также прямая торговля голосами (купля-продажа необходимого числа голосов, требуемого для принятия решения, выгодного группе интересов).

Последний метод, который можно предложить, носит название ранжирование альтернатив, или голосование де Борда. Пусть каждый избиратель припишет число 1 наихудшей альтернативе, 2 – следующей (менее худшей), 3 – следующей и т.д. Пусть #(Θ) – общее число баллов, приписанное состоянию Θ, тогда можно отметить, что состояние Θ выше Θ΄ тогда и только тогда, когда #(Θ) > #(Θ΄). Очевидно, что использование #(Θ) дает полное транзитивное упорядочивание, которое напрямую зависит от системы баллов, приписываемых голосам. Например, если вместо системы баллов [1,2,3,4] использовать систему [1,2,4,8], то может возникнуть другое социальное упорядочивание. При этом отбрасывая некоторые из худших альтернатив при доступности «наилучших состояний», они перестают быть «наилучшими» и изменяют систему не только ранжирования, но и показывают взаимозависимость всех альтернатив.

Для примера приведем выбор Международным олимпийским комитетом места проведения игр в 2000 г. В каждом столбце табл. 5 показан раунд голосования с исключением наихудшего выбора после каждого раунда.

Таблица 5

Раунд
Сидней
Пекин
Манчестер				–
Берлин			–	–
Стамбул		–	–	–

 

Очевидно, что преимущество Сиднея над Пекином определяется тем, присутствует ли в ранжировании Манчестер, что еще раз подчеркивает нарушение независимости альтернатив.

Приведенные системы голосования показывают, что в каждом из вариантов голосования существует невозможность создания единой функции благосостояния, удовлетворяющей всех членов общества. Для определения функции как таковой необходимо, чтобы она как минимум обладала следующими возможностями, о которых написал Эрроу.

1. Универсальность.

Критерий общественных предпочтений должен определяться логически для всех возможных индивидуальных предпочтений.

Данное условие утверждает, что функция общественного благосостояния может порождать упорядоченные общественные предпочтения независимо от того, какими оказываются индивидуальные отношения предпочтения. По сути речь идет о том, что механизм общественного выбора не должен зависеть от индивидуума. Таким образом, если учитывать это условие, а также требование транзитивности, механизм голосования по принципу большинства прекращает свое действие.

2. Единогласие по Парето.

Критерий единогласия по Парето означает следующее – в мире двух состояний Ϛ и Ϛ¹, из которых каждый индивид предпочитает Ϛ, будет приниматься именно это решение уже и с позиции общества в целом.

3. Независимость от посторонних альтернатив.

Если индивиды принимают данное ранжирование предпочтений двух товаров, то появление третьего товара не изменяет данного ранжирования, точно также себя ведет и общество в целом.

4. Отсутствие диктатуры.

Не существует индивида, голос в процессе принятия общественных решений является решающим. Таким образом, исключается лишь наиболее экстремальная и абсолютная форма диктатуры. При этом допускается существование так называемого квазидиктатора, который добивается своего по всем социальным альтернативам, кроме одной пары предпочтений.

Исходя из данных аксиом, вытекает знаменитая теорема о невозможности Эрроу, которая гласит о том, что построение по данным аксиомам единой функции общественного благосостояния не представляется возможным, только если данное общество не состоит из одного индивида, или не является диктатурой.

При этом сама теорема Эрроу не утверждает, что функции общественного благосостояния не существует – не существует именно функции, которая подчинялась бы всем аксиомам. Утверждается лишь то, что невозможно создать единое правило для нахождения «общественной воли», то есть тяжело создать механизм, одновременно удовлетворяющий правилам честного ранжирования, простоте и зависимости от индивидуальных предпочтений.

Строгое доказательство теоремы было предоставлено в работе Геанокоплоса в 1996 г.

1 этап доказательства. Предположим, что существует некое социальное состояние с. Предположим, что в предпочтениях индивида это состояние занимает последнее место. Тогда согласно аксиоме о единогласии по Парето это состояние должно быть последним и в общественных предпочтениях.

2 этап доказательства. Представим, что социальное состояние χ перемещается на первое место для 1 индивида, причем положение остальных социальных состояний остается неизменным. Предположим теперь, что индивид 2 приходит к такому же выводу в отношении социального состояния χ в силу каких-то собственных ощущений. Можно повторить такое рассуждение для каждого последующего потребителя, и, если принять во внимание возможность индивидуальных предпочтений влиять на общественные, в конце концов социальное состояние χ окажется на вершине общественных предпочтений. При этом индивид, который является первым в списке изменивших общественное предпочтение, оказывается основным игроком в этом процессе голосования.

Предпринималось много попыток ослабить требования Эрроу к функции общественного благосостояния. Одним из таких приемов является создание этической концепции благосостояния, предложенной Роулзом в 1971 г. Роулз вводит дополнительные этические соображения о функции общественного благосостояния.

1. Анонимность. Пусть ú – N вектор полезностей и пусть û – другой вектор, полученный из ú путем перестановки некоторых элементов. Тогда W(ú)= W(û).

Речь идет о том, что необходимо ранжировать социальные состояния не на основе индивидуальных предпочтений, а в зависимости от их уровня благосостояния.

2. Равенство по Хаммонду. Пусть ú и û – два различных N-мерных вектора полезностей. Предположим, что úк = ûк для всех к, кроме i и j. Если ûi > úi >új >ûi, то W(ú) >W(û). Оно отражает тот факт, что общество предпочитает снижение дисперсии полезностей различных индивидов.

3. Сепарабельность. Данное условие предполагает независимость предельной нормы замещения между двумя индивидами от благосостояния остальных граждан.

В этической системе, предложенной Роулзом, за основу принятия решений берется благосостояние наибеднейшего гражданина. В ней автор отказывается от основных условий Эрроу, оставляя лишь необходимость следовать принципу Парето. В результате чего появляется максиминная функция благосостояния, схожая с комплементарной функцией в теории потребления: W=min{û;ú}.

Рис. 1

 

Вторая функция, названная в честь философа Ницше, является максимаксной функцией W=max{û;ú}. Согласно данной функции благосостояния общественный выбор определяется в первую очередь благосостоянием самого богатого индивида. Однако данная функция не отвечает критериям этического порядка Хаммонда, а именно выбор, оптимизирующий данную функцию, всегда исключает одного потребителя из рассмотрения и тем самым заведомо делает диктатором одного потребителя. График ее представлен на рис. 2.

 

 

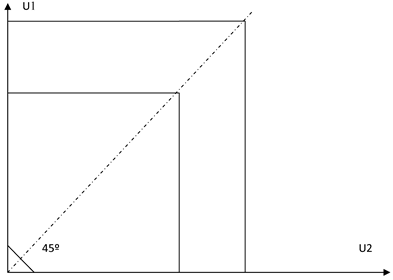
Рис. 2

 

Третьей функцией, которая может быть использована в качестве функции, описывающей общественное благосостояние, является утилитаристская функция. Эта функция удовлетворяет условию равенства по Парето и условию анонимности (рис. 3).

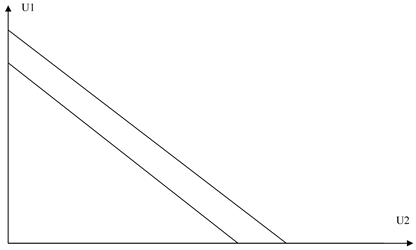
Рис. 3

Обобщая вышеназванные функции, можно сказать, что функция общественного благосостояния должна принадлежать к семейству функций с постоянной эластичностью замещения (CES-функций):

,

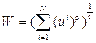где 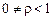, а 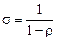– постоянная и одинаковая для всех индивидуумов эластичность замещения между двумя любыми индивидами.

Это очень гибкая функция общественного благосостояния. Различные значения ρзадают различную степень «кривизны» общественных кривых безразличия и таким образом учитывают степень, в которой в распределении доходов ценится равенство. Действительно, утилитаристскую функцию, которая подразумевает полное безразличие общества к вопросам распределения доходов, можно рассматривать как предельный случай при ρ → 1 (σ → ∞). При ρ → – ∞ (σ →0) стремится к роулсианскому виду, где имеет место абсолютный сдвиг общества в сторону равенства. Возможные варианты изображены на графиках (рис. 4):

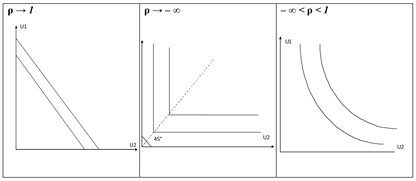
Рис. 4

 

Функцию общественного благосостояния можно рассматривать также и в макроэкономическом аспекте, для этого необходимо посмотреть, как изменяется уровень благосостояния при небольших изменениях в распределении. Допустим, нам задана утилитаристская функция, и потребление каждого блага каждым домохозяйством изменяется на величину 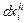. Отсюда

.

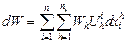Предположим, что государство может выбрать распределение 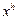при общем ограничении

.

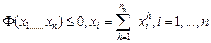Для любой пары товаров, потребляемой любыми двумя домохозяйствами, получим 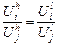и в дополнение к нему получаем 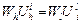(при условии, что все издержки на производство товаров идентичны).

Если при данной функции общественного благосостояния каждое домохозяйство максимизирует свою полезность при бюджетном ограничении 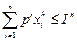, то можно подставив функцию спроса в функцию полезности получить неявную функцию полезности каждого домохозяйства, уже зависящую от уровня цен в экономике: 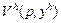, что, в свою очередь, дает возможность представить функцию общественного благосостояния как зависимость от цен и доходов населения:

.

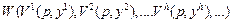Вспомним, что в точке потребительского выбора на свободном рынке мы имеем , где величина 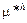– предельная полезность денежного дохода для домохозяйства h, равная 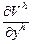. Таким образом, для случая рыночной экономики условие общественного оптимума можно переписать так: 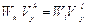для любой пары названных домохозяйств. По сути мы наблюдаем эффект роста общественного благосостояния от передачи одного доллара в точке оптимума (обозначим его буквой М). Отсюда напрямую вытекает, что если имеется какое-то изменение в экономике, влияющее на индивидуальные доходы (например, изменение количества природных ресурсов или технологии), то изменение общественного благосостояния имеет вид:

= = ,

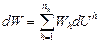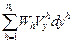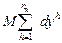где правая часть отражает изменение национального дохода.

Рассмотрим изменение в ценах р при неизменных доходах 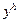. Дифференцируя функцию общественного благосостояния, получим, что воздействие на общественное благосостояние равно: 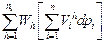. Но поскольку предполагается, что каждое домохозяйство максимизирует полезность, то согласно тождеству Роя – – получим следующее равенство:

= ,

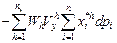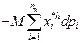что можно охарактеризовать как стоимость агрегированных расходов. В то же время агрегированные расходы в макроэкономической интерпретации представляют собой показатель национального дохода. Таким образом, в микроэкономике возникает глубоко макроэкономический вопрос распределения данного национального дохода.

При этом необходимо создать критерий распределения, который бы позволил, не нарушив критерий эффективности по Парето, оптимально распределить имеющиеся ресурсы в условиях неравномерных индивидуальных функций полезности. Один из возможных методов – это аккумулировать все желаемые результаты с позиции основного принципа эффективности, который для общества часто носит название «равенство» или «справедливости».

Само по себе понятие справедливости уже несет в себе проблемный характер, так как связано скорее не с экономической сферой, а с понятиями, далекими от экономики, а именно моралью и нравственностью.

Однако для того, чтобы не участвовать в разборке нравственных категорий, необходимо попытаться ввести в эту глубоко нравственную тему некую экономическую интерпретацию: путь распределения будет тогда справедливым, если в обществе никто не желает иметь чей-нибудь потребительский набор вместо своего, то есть в обществе отсутствует понятие зависти. Такое распределение будет не только справедливым, но и эффективным по Парето.

В этом случае распределение может осуществляться по принципу равенства полезностей двух и более полезностей, или иначе говоря, точка оптимума будет располагаться на серединном луче в плоскости двух полезностей (рис. 5):

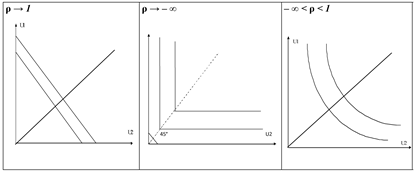
Рис. 5

 

Еще одна концепция справедливого распределения изложена в работах Харшаньи и Роулза. А именно под справедливым распределением и Харшаньи и Роулз принимают положение о том, что справедливым критерием общественного благосостояния должен быть такой, который выбрал бы рациональный человек, если бы судил по справедливости. Чтобы обеспечить «справедливость» его решения, они вводят понятие исходного состояния (скрытого, по выражению Роулза, «покровом неведения»), в котором индивид обдумывает свой выбор, не зная о том, какие роль и место в обществе будут отведены ему на самом деле. Таким образом, оба эти автора предполагают, что этот выбор делается в условиях неопределенности относительно того, кем человек в итоге станет в обществе, создаваемом по его видению. Однако взгляды Харшаньи и Роулза на правило, которое определяет выбор индивида в «исходном состоянии», различаются.

Харшаньи предполагает, что каждый рациональный индивид действует в условиях неопределенности согласно функции фон Неймана–Моргенштерна. Тогда предпочтения можно представить как функцию неопределенности, считая, что в качестве полезностей выбора находятся социальные функции предпочтений. Затем согласно принципу недостаточного обоснования он предполагает, что рациональный индивид в исходном состоянии оценивает возможность оказаться на месте любого члена общества как равновероятную (т.е. если в обществе N членов, то вероятность составляет 1/N), что позволяет выписать функцию полезности следующим образом:

.

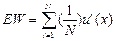При общественном выборе между состояниями х и у должно предпочитаться то из них, которое имеет более высокую ожидаемую полезность, т.е.: 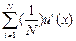> 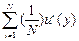, что соответствует утилитаристскому критерию.

Роулз отвергает утилитаристское правило Харшаньи по нескольким причинам. В частности, он отрицает назначение каких бы то ни было вероятностей одинаковых или нет, потому что один индивид окажется на чужом месте, поскольку в исходном для этого нет эмпирических оснований. Таким образом, Роулз отвергает саму идею выбора на основе ожидаемой полезности. Вместо этого он рассматривает проблему выбора в исходном состоянии как проблему выбора при полном неведении. Предполагая, что люди не склонны к риску, он доказывает, что при полном неведении рациональный индивид будет ранжировать социальные состояния, основываясь на том, как бы он их оценил с позиции самого бедного члена общества. Тем самым состояние х предпочитается у, если:

min{u1(x)…..;un(x)}> min{u1(y)…..;un(y)},

т.е. в соответствии с критерием максимина.

При этом Эрроу показал, что оба эти критерия являются абсолютно совместимыми. Для доказательства этого факта он берет произвольную функцию полезности на социальных состояниях в условиях определенности ui(x). Эти же самые предпочтения можно представить и с помощью положительного монотонного преобразования 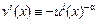, где α>0. Теперь предположим, что функция vi(x) – функция полезности фон Неймана–Морген-
штерна на неопределенных исходах. Легко убедиться, что степень несклонности к риску, демонстрируемая vi(x), возрастает по параметру α. Предположим, как это делает Харшаньи, что: 1) вероятность оказаться в положении любого индивида одинакова; 2) социальные состояния ранжируются каждым индивидом в соответствии с его ожидаемой полезностью; 3) функция общественного благосостояния имеет вид:

W=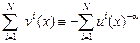

или при монотонном преобразовании имеет вид

W*= .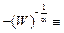

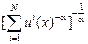При 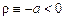это выражение полностью соответствует условию Харшаньи.

 

 

[1] Скитовски Т. Суверенитет и рациональность потребителя. В кн.: Вехи экономической мысли. СПб. Т. 1. С. 370.

[2] Алле М. Поведение рационального человека в условиях риска: критика постулатов американской школы// THESIS. 1994 – №5. С. 227.

[3] Беккер Г. Экономический анализ и человеческое поведение // THESIS. Зима. 1993. Т. 1. Вып. 1. 1993, с. 26.

[4] Скитовки Т. Суверенитет и рациональность потребителя. В кн.: Вехи экономической мысли. СПб. Т. 1. С. 372.

[5] Там же. С. 374.

[6] Теория потребительского поведения и спроса (Серия «Вехи экономической мысли». Вып. 1). Под ред. В.М. Гальперина. – СПб.: Экономическая школа, 1993. С. 333.

[7] Гальперин В.М., Игнатьев С.М., Моргунов В.И. Микроэкономика. Т. 1. СПб.: Экономическая школа, 1996. С. 160–161.

[8] В СССР сходный подход к анализу и прогнозированию потребительского спроса разрабатывала в Новосибирске группа под руководством К.К. Вальтуха.

[9] Теория потребительского поведения и спроса (Серия «Вехи экономической мысли». Вып. 1). Под ред. В.М. Гальперина. СПб.: Экономическая школа, 1993. С. 333–326.

[10] K. Lancaster. A new approach to consumer theory// Journ. Polit. Econ. 1966. Vol. 74, #2.

K. Lancaster. Consumer demand: A new approach. New York. 1991.

[11] Там же. С. 327.

[12] Теория потребительского поведения и спроса (Серия «Вехи экономической мысли». Вып. 1). Под ред. В.М. Гальперина. СПб.: Экономическая школа, 1993. С. 328.

[13] Ланкастер К. Математическая экономика М.: Изд-во «Советское радио». С. 126.

[14] Ланкастер К. Математическая экономика / Пер. с англ. под ред. Д.Б. Юдина. М.: Советское радио, 1972. С. 126.

[15] Ланкастер К. Математическая экономика Пер. с англ. под ред. Д.Б. Юдина. М.: Советское радио, 1972. с. 129.

[16] Там же С. 130.

[17] Фридман А.А. Лекции по курсу микроэкономического уровня продвинутого уровня. М.: Издательский дом ГУ ВШЭ, 2008. С. 154.

[18] Вальрас Л. Элементы чистой политической экономии, или Теория общественного богатства. М.: Изограф, 2000.

[19] Блауг М. 100 великих экономистов до Кейнса. М.: «Экономикус», 2008. С. 57.

[20] Чеканский А.Н., Фролова Н.Л. Микроэкономика. Промежуточный уровень. М.: ИНФРА-М, 2005. С. 548–549.

[21] Чеканский А.Н., Фролова Н.Л. Микроэкономика. Промежуточный уровень. М.: ИНФРА-М, 2005. С. 556.

[22] Френсиса Исидора Эджуорта (1845–1926) принято считать экономистом для экономистов. Он автор многочисленных технических эссе по широкому кругу экономических проблем: начиная с вопросов ценообразования в условиях монополии, заканчивая чистой теорией международной торговли. Его наиболее масштабное сочинение «Математическая психология» («Mathematical Psychics», 1881) содержало идеи, опережавшие время и нелегко воспринималось современниками. Так, например, в нем использовались кривые безразличия и понятие «ядра» меновой экономики, которые вошли в широкий научный обиход намного позднее. М. Блауг называет теорию «ядра» меновой экономики прекраснейшим вкладом Ф.И. Эджуорта в экономическую теорию и описывает ее следующим образом: «Вообразите группу торговцев, имеющих некоторые начальные запасы товаров и настроенных на обмен при том, что пока отсутствует рынок или какое-то его подобие; эти торговцы могут действовать поодиночке или образовывать блоки или коалиции, чтобы улучшить свое исходное положение; разрешено все, но каждый торговец должен добровольно принять любой окончательный результат торговли. Затем Эджуорт показывает, что в предельном случае, когда количество торговцев увеличивается, «ядро» окончательного распределения товаров, достигнутого в результате единогласно согласованной системы сделок, оказывается идентичным тому множеству равновесных запасов товаров, которое генерирует ценовая система в условиях совершенной конкуренции». Блауг М. 100 великих экономистов до Кейнса. М.: «Экономикус», 2008. С. 337–338.

[23] Патинкин Дон. Деньги, процент и цены. М.: Экономика, 2004.

[24] Вальрас Л. Элементы чистой политической экономии, или Теория общественного богатства. М.: Изограф, 2000.

[25] Блауг М. 100 великих экономистов до Кейнса. СПб.: Экономикус, 2008. С. 56, 57.

[26] Arrow K. J., Debreu G. Existence of an equilibrium for a competitive economy // Econometrica, 1954, v. 22, №3.

[27] McKenzie L.W. On the existence of general equilibrium for a competitive market. //Econometrica, 1959, 27, pp. 54–71.

[28] В экономике обмена все потребители имеют локально ненасыщаемые, непрерывные, строго выпуклые предпочтения и положительные начальные запасы каждого блага.

[29] Фридман А.А. Лекции по курсу микроэкономического уровня продвинутого уровня. М.: Издательский дом ГУ ВШЭ, 2008. С. 195.

[30] Розанова Н.М. Микроэкономика. Руководство для будущих профессионалов. М.: Юрайт, 2012. С. 889.

[31] Микроэкономика. Под общей редакцией В.М. Гальперина. Т.1. СПб.: «Экономическая школа», 1996. С. 51–52.

[32] Микроэкономика. Под общей редакцией Гальперина. СПб.: «Экономическая школа», 1996. Т. 2. С. 306–307. Fisher I. The Nature of Capital and Income. New York, 1927. Р. 52.

[33] Микроэкономика. Под общей редакцией В.М. Гальперина. СПб.: «Экономическая школа», 1996. Т. 2. С. 308.

[34] Кейнс Дж. М. Общая теория занятости, процента и денег. М.: «Прогресс», 1978. М. 202.

[35] Хайман Д.Н. Современная микроэкономика: анализ и применение. М.: Финансы и статистика, 1992. С. 203.

[36] Розанова Н.М. Микроэкономика. Руководство для будущих профессионалов. М.: Юрайт, 2012. С. 787–788.

[37] Рынок капитала состоит из кредитного рынка и рынка корпоративных ценных бумаг, причем кредитный рынок подразделяется на денежный рынок и рынок государственных облигаций.

[38] Schultz T.W. Investment in human capital: the role of education and of research. – New York; London: The Free press; Macmillan, 1971, p. 57.

[39] Weisbrod B.A. The valuation of human capital // Journal of political economy. – Chicago (Ill.): The University of Chicago press, 1961. – Vol. 69, №5, p. 426–428, 430–434.

[40] Это тождество можно рассматривать как формализацию ветхозаветной максимы, согласно которой человек «как вышел … нагим из утробы матери своей, таким и отходит, каким пришел, и ничего не возьмет от труда своего, что мог бы он понести в руке своей…» (Библия: книги священного писания Ветхого и Нового Завета. М.: Российское библейское общество, 2002. – Ветхий Завет. Книга Екклесиаста, или Проповедника. Глава 5. – С. 621).

[41] Беккер Г.С. Экономический анализ и человеческое поведение // Теория и история экономических и социальных институтов и систем (THESIS), 1993. Т. 1. Вып. 1. С. 28.

[42] Микроэкономика. Под общ. ред. В.М. Гальперина. СПб.: Экономическая школа, 1996. Т. 2. с. 326.

[43] Samuelson P.A. Dynamic process analysis. – В сб. [Collected papers]. – Т. 1, с. 597–598; еще один способ получения множителя e^rt приведен в работе: Фалин Г.И. Математические основы теории страхования жизни и пенсионных схем. М.: Изд-во мех.-мат. ф-та МГУ, 1996. – С. 8–11.

[44] Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. 3-е изд. М.: Дело и сервис, 2001. С. 198.

[45] Samuelson P.A. Collected papers. – Т.1. С. 161–188.

[46] Samuelson P.A. Collected papers. – Т. 1, с. 161–188.

[47] Если , то К будет фиксированной величиной, и чистые инвестиции будут равны нулю (разрыв между фактическим и желаемым запасом капитала не будет сокращаться).

Если , то этот разрыв будет преодолен в течение одного (t-го) периода и желаемый запас капитала будет достигнут. Другими словами, будет происходить мгновенная настройка.

[48] Если , то фактический запас капитала будет отдаляться от оптимального.

[49] Слово «вечный» используется, т.к. при постоянно-экспоненциальном износе объем производимых данным оборудованием услуг стремится к нулю, но никогда не достигает, таким образом, амортизируемое оборудование навсегда остается в составе основных фондов.

[50] Кейнс Дж. М. Общая теория занятости, процента и денег. М.: Прогресс, 1978. С. 218, 219, 222–224.

[51] Богл Джон К. Битва за душу капитализма. М.: Издательство Института Гайдара, 2011. С. 143.

[52] Там же. С. 10.

[53] Там же. С. 31.

[54] Найт Ф.Х. Теория вероятности и математическая статистика. М.: Дело, 2003.

[55] Ф. Найт проводит различие между собственно риском и неопределенностью. Он выделяет типичные ситуации исчислимого риска. Во-пер-
вых, это ситуации, в которых известна априорная вероятность, например азартные игры. Во вторых, ситуации, в которых известна статистическая вероятность, например вероятность человека дожить до определенного возраста, которая рассчитывается компаниями по страхованию жизни. Такие риски вполне можно вычислить, от них можно застраховаться и включить страховые взносы в издержки функционирования. Другое дело – подлинная неопределенность, для которой характерно отсутствие не только вероятностей, но даже полного описания во