 |
Главная |
Этапы решения задачи 1
|
из
5.00
|
1. Уравнивание углов.
2. Вычисление дирекционных углов и румбов.
3. Вычисление и уравнивание приращений координат.
4. Вычисление координат точек хода.
5. Построение плана теодолитного хода в масштабе 1 : 500.
6. Вычисление разбивочных элементов плановой привязки здания.
Решение задачи:
1. Уравнивание углов.
Подсчитываем сумму внутренних углов теодолитного хода 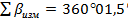 .
.
Теоретическая сумма углов в многоугольнике находится по формуле
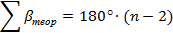
где 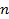 - количество углов многоугольника.
- количество углов многоугольника.
В нашем случае теоретическая сумма углов равна
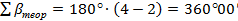 .
.
Разность практической суммы углов 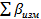 и теоретической суммы
и теоретической суммы  даёт ошибку измерения углов
даёт ошибку измерения углов 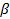 , которая называется угловой невязкой
, которая называется угловой невязкой 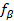
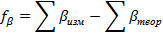
 .
.
Далее необходимо сравнить полученную невязку с допустимым значением 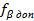
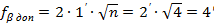 .
.
Получаем, что 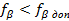 , т.е.
, т.е. 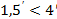 . Следовательно углы измерены с необходимой точностью.
. Следовательно углы измерены с необходимой точностью.
Угловую невязку необходимо распределить между измеренными углами с противоположными знаками, в первую очередь в углы с десятыми долями минут, а при наличии целых минут – в углы, заключенные между наиболее короткими сторонами.
Исходные данные и исправленные углы 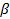 записывают в ведомость координат (приложение 1).
записывают в ведомость координат (приложение 1).
2. Вычисление дирекционных углов и румбов.
По исходному дирекционному углу 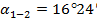 вычисляем дирекционные углы последующих направлений по формулам
вычисляем дирекционные углы последующих направлений по формулам
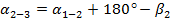

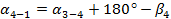
Для контроля высчитываем  .
.
В нашем примере дирекционные углы равны
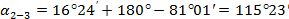
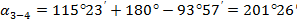
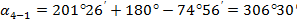
|
Контроль 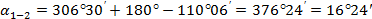
Вычисленные дирекционные углы вносят в ведомость координат теодолитного хода (приложение 1).
Далее полученные дирекционные углы переводим в румбы:
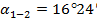
| 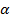 лежит в 1 четверти лежит в 1 четверти
| 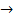
| 
|
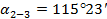
| 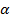 лежит во 2 четверти лежит во 2 четверти
| 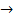
| 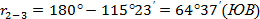
|

| 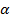 лежит в 3 четверти лежит в 3 четверти
| 
| 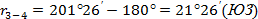
|
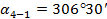
| 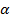 лежит в 4 четверти лежит в 4 четверти
| 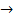
| 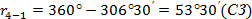
|
3. Вычисление и уравнивание приращений координат.
По румбам и горизонтальным проложениям линий вычисляем приращения координат:

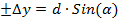
Вычисление приращений координат производится с помощью калькулятора или таблиц Брадиса с точностью до 4 знаков после запятой, а при записи в ведомость координат до 0,01 м.
Вычисляем приращения координат для нашего примера (приложение 1).
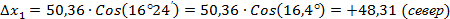
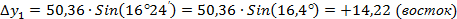
Примечание: при вычислении косинусов и синусов углов необходимо минуты и секунды перевести в доли градуса. В 1 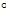 содержится 60
содержится 60 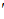 , значит 24
, значит 24 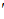 будут равны 0,4
будут равны 0,4 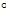 (24
(24 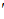 : 60
: 60 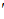 = 0,4
= 0,4 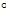 ).
).
Также необходимо обращать внимание на знаки приращений координат, которые зависят от направления румба
| 
| |
| СВ | + | + |
| ЮВ | - | + |
| ЮЗ | - | - |
| СЗ | + | - |
Аналогично находим остальные приращения координат.
Далее подсчитываем алгебраическую сумму приращений координат
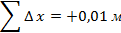
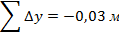
Теоретическая сумма приращений должна быть равна нулю.
Разница практики и теории даёт линейные невязки по осям X и Y.
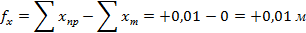
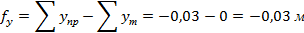
Далее вычисляем абсолютную линейную невязку:
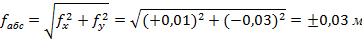
Вычисляем относительную линейную невязку и сравниваем её с допустимой величиной ( 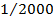 )
)
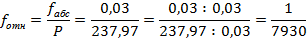
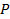 - периметр теодолитного хода, т.е. сумма всех расстояний.
- периметр теодолитного хода, т.е. сумма всех расстояний.
 :
: 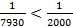
Значит, условие выполняется.
Линейные невязки распределяем с обратным знаком в вычисленные приращения:
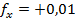 , поправку -0,01 вносим в в большее расстояние между опорными точками (в примере в
, поправку -0,01 вносим в в большее расстояние между опорными точками (в примере в  .
.
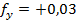 , поправки по +0,01 вводим в наиболее длинные стороны.
, поправки по +0,01 вводим в наиболее длинные стороны.
После введения поправок заносим полученные данные в ведомость координат (приложение 1).
Далее приступаем к вычислению координат опорных точек:

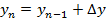
В нашем примере:

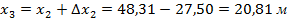

|
Для контроля вычисляем координаты начальной точки 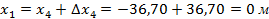
Аналогично производятся вычисления координат точек по 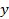 .
.
Полученные координаты записываем в ведомость координат (приложение 1).
Пользуясь значениями вычисленных координат наносим опорные точки на план в масштабе 1 : 500. Для этого необходимо на чертежной или миллиметровой бумаге формата А4 вычертить координатную сетку квадратов размерами  см и произвести оцифровку координат по осям
см и произвести оцифровку координат по осям  и
и  .
.
Полученные на плане точки необходимо соединить прямыми линиями и указать значения румбов и горизонтальных проложений сторон теодолитного хода (приложение 2).
Примечание:
1). Координатная сетка должна быть нанесена тонкими линиями зеленого цвета.
2). Точки соединить линиями толщиной 1-2 мм тушью или в карандаше.
3). Диаметр точек теодолитного хода в масштабе 1 : 500 должен быть не более 2 мм.
Далее на плане теодолитного хода накладываем контур здания размерами 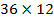 м (например параллельно стороне 2-3), два угла которого привязываем к опорным точкам ближайшей стороны теодолитного хода полярным способом (угол В к точке 2, угол С – к точке 3).
м (например параллельно стороне 2-3), два угла которого привязываем к опорным точкам ближайшей стороны теодолитного хода полярным способом (угол В к точке 2, угол С – к точке 3).
Для плановой привязки углов здания к опорным точкам необходимо решить 2 обратные геодезические задачи и вычислить разбивочные элементы β и d.
2 – В:
По плану в масштабе 1 : 500 измеряем координаты 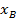 и
и 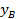 , а координаты точки 2 берем из ведомости координат:
, а координаты точки 2 берем из ведомости координат:
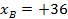
| 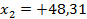
|
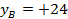
| 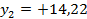
|
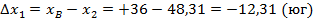
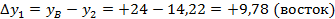
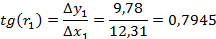
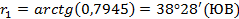
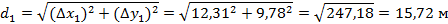
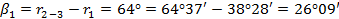
3 – C:
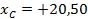
| 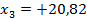
|
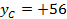
| 
|
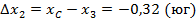
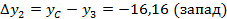

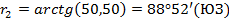
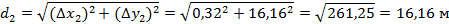
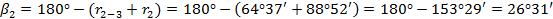
Получаем разбивочные элементы:
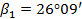
| 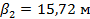
|
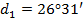
| 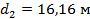
|
Приложения к задаче 1:
1). Ведомость координат замкнутого теодолитного хода – приложение 1.
2). План по координатам с плановой привязкой здания в масштабе 1 : 500 – приложение 2.
Задача 2. Вертикальная планировка строительного участка с составлением картограммы земляных работ, подсчетом объемов земляных масс и вертикальная привязка здания на плане с горизонталями.
[Литература: Л-1 (9-3); Л-2 (§96, 97); Л-3 (§43, 44, 55-59); Л-4 (§26)].
По плану вертикальной планировки составить:
1). Картограмму земляных работ и произвести подсчёт объемов земляных масс с вычисление баланса земляных работ в %.
2). План участка в горизонталях с вертикальной привязкой здания.
Исходные данные:
1. Схема нивелирования по квадратам (стороны квадрата 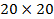 м).
м).

2. Отметка репера равна № варианта учащегося (задаёт преподаватель).
3. Продольный уклон планировки – 0,02, поперечный уклон – 0,01.
4. Высота сечения рельефа на плане в горизонталях равна 0,25 м.
Этапы решения задачи 2:
1. Вычисление черных, проектной и рабочих отметок.
2. Составление картограммы земляных работ.
3. Вычисление объемов земляных масс с подсчетом баланса земляных работ.
4. Составление плана участка в горизонталях.
5. Вертикальная привязка здания к строительной площадке.
Решение задачи:
1. Вычертить на миллиметровой бумаге размером 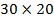 см схему нивелирования в произвольном масштабе (по исходным данным) и картосхему из 6 квадратов в масштабе 1 : 500 (квадрат
см схему нивелирования в произвольном масштабе (по исходным данным) и картосхему из 6 квадратов в масштабе 1 : 500 (квадрат 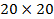 ). Пронумеровать вершины квадратов слева направо и сверху вниз от 1 до 12 (см. приложение №3).
). Пронумеровать вершины квадратов слева направо и сверху вниз от 1 до 12 (см. приложение №3).
2. Используя отметку репера, отсчёт a по рейке над репером и отсчёты по рейке, устанавливаемой над каждой вершиной, вычислить черные отметки (отметки земли) через горизонт прибора.
Рассмотрим этот процесс на примере (см. приложение №3).
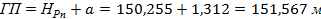
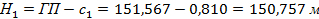

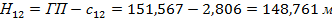
Полученные отметки вершин квадратов с 1 по 12 округлить до сотых и вписать на картосхему (приложение 3).
3. Вычислить проектную отметку (красную отметку) горизонтальной плоскости площадки по формуле:
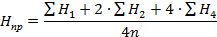
где 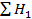 – черные отметки, входящие в один квадрат,
– черные отметки, входящие в один квадрат, 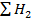 - черные отметки, входящие в два квадрата,
- черные отметки, входящие в два квадрата,  - черные отметки, входящие в четыре квадрата,
- черные отметки, входящие в четыре квадрата,  - число всех квадратов.
- число всех квадратов.
В нашем примере:

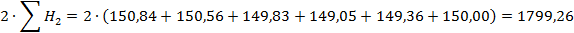
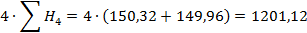
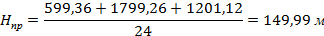
Проектную отметку вписать на картосхему над черными отметками красным цветом в каждой вершине (приложение 3).
4. Вычислить рабочие отметки для каждой вершины квадратов:

В примере:
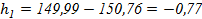 ,
,
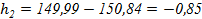 ,
,
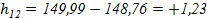
Если знак рабочей отметки «+», то это насыпь, если «-», то это выемка. Рабочие отметки вписываются под черными отметками в каждой вершине.
Рабочие отметки необходимо вписать синим цветом под черными отметками в каждой вершине (приложение 3).
5. Определить местоположение точек нулевых работ.
Указанные точки определяются на сторонах квадратов, имеющих противоположные знаки рабочих отметок. Расстояние  до точек нулевых работ вычисляется по формуле
до точек нулевых работ вычисляется по формуле

где 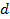 - длина стороны квадрата (в примере 20 м),
- длина стороны квадрата (в примере 20 м), 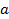 - рабочая отметка вершины квадрата, от которой определяется
- рабочая отметка вершины квадрата, от которой определяется  ,
, 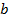 - рабочая отметка другой вершины данной стороны квадрата.
- рабочая отметка другой вершины данной стороны квадрата.
Значения рабочих отметок в формуле берутся без учета знаков (+/-), т.е. по модулю.
Рассмотрим стороны 10 – 6, 6 – 7:
 ,
, 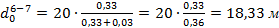
Полученные значения расстояний  откладывают в масштабе на соответствующих сторонах квадратов на картограмме, после чего точки соединяют под линейку прямыми линиями. Эти линии называются линиями нулевых работ (границами между насыпями и выемками). Полученные фигуры нумеруют слева направо и сверху вниз. Площади фигур оформляют условными знаками или в цвете (розовый фон – насыпь, желтый – выемка).
откладывают в масштабе на соответствующих сторонах квадратов на картограмме, после чего точки соединяют под линейку прямыми линиями. Эти линии называются линиями нулевых работ (границами между насыпями и выемками). Полученные фигуры нумеруют слева направо и сверху вниз. Площади фигур оформляют условными знаками или в цвете (розовый фон – насыпь, желтый – выемка).
6. По составленной картограмме земляных работ подсчитывают объем насыпей и выемок грунтов для каждой фигуры по формуле 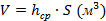 , где
, где  - средняя рабочая отметка данной фигуры (м),
- средняя рабочая отметка данной фигуры (м), 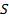 - площадь данной фигуры (
- площадь данной фигуры ( 
7. Определение средних рабочих отметок  .
.
Фигура №9: 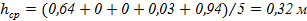
Фигура №1: 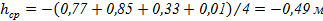
Фигура №8: 
Подсчитывают все 10 средних рабочих отметок и вписывают их в таблицу подсчета объемов земляных масс.
Примечание: фигуру 3 из-за своей малой величины можно отбросить, а фигуру 2 считать четырехугольником.
8. Вычисляют площади фигур.
Т.к. один квадрат 20×20 м, то 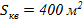 . В нашем примере фигуры 1,2 и 10 будут иметь площадь
. В нашем примере фигуры 1,2 и 10 будут иметь площадь 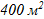 .
.
игура №4 – трапеция: 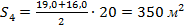 . Поэтому площадь фигуры №5 будет равна
. Поэтому площадь фигуры №5 будет равна 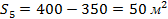 , т.к. фигуры 4 и 5 вместе составляют квадрат (
, т.к. фигуры 4 и 5 вместе составляют квадрат ( 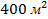 ).
).
Фигура №8 – треугольник: 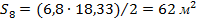 . Значит
. Значит 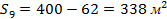 .
.
Подсчитав площади всех фигур, их значения заносят в таблицу подсчета объемов земляных масс.
Примечание:
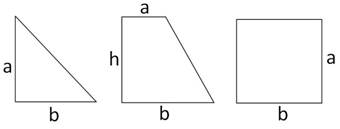
Площади элементарных фигур:
1). Треугольник - 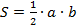
2). Трапеция – 
3). Квадрат – 
9. Перемножаем  и площади фигур и получаем объемы насыпи и выемки.
и площади фигур и получаем объемы насыпи и выемки.
| № фигур | Средняя раб. отм. 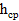
| Площади фигур, м2 | Объемы, м3 | |
| Выемка (-) | Насыпь (+) | |||
| -0,49 | ||||
| -0,43 | ||||
| -0,30 | ||||
| +0,05 | 2,5 | |||
| -0,11 | 70,5 | 7,8 | ||
| +0,36 | 329,5 | 118,6 | ||
| -0,11 | 6,8 | |||
| +0,32 | 108,2 | |||
| +0,59 | ||||
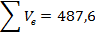
| 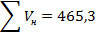
|
Примечание: фигура №3 исключена из подсчётов из-за своей малости.
Подсчитываем баланс земляных работ:
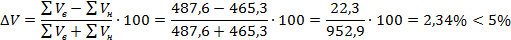
10. Составляется план участка местности в горизонталях.
- на миллиметровую бумагу наносят сетку квадратов в масштабе 1 : 500.
- наносят на план горизонтали с высотой сечения рельефа 0,25 м.
Использую аналитический способ, определяют расстояния от вершин квадратов до точек, где пройдут горизонтали при заданном сечении рельефа.
Сторона квадрата 1 – 5: разность отметок 1 и 5 точек составляет 0,76 м (158,76 – 150,00), которое приходится на длину линии 1 – 5 на плане равную 40 мм. Если идти от 5й точки к 1й, то кратными сечению будут отметки точек 150,25, 150,50, 150,75 м. Решаем пропорцию и находим расстояние на стороне квадрата через каждые 0,25 м.
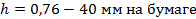
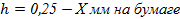
Отсюда  .
.
Таким образом, отложив по линии 1 – 5 три расстояния по 13 мм, мы получим выходы горизонталей 150,25, 150,50 и 150,75 м.
Проинтерполировав по всем сторонам квадратов, соединяют одноименные отметки, нанося тем самым горизонтали на план.
11. Оформляют план в горизонталях. Горизонтали проводятся коричневым цветом.
12. Произвести вертикальную планировку здания к строительной площадке.
Для этого необходимо:
1). Нанести на план в горизонталях здание размерами 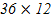 м в масштабе 1 : 500 примерно в середине участка.
м в масштабе 1 : 500 примерно в середине участка.
2). Определить черные отметки углов здания по горизонталям.
В нашем примере: 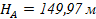 ,
, 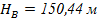 ,
,  ,
,  .
.
3). Определить диагональ здания (АС или BD) с наибольшим перепадом высот:
А – С: 150,16 – 149,97 = 0,19 м
B – D: 150,44 – 149,65 = 0,79 м.
Выбираем диагональ BD и вычисляем отметку планировки 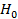
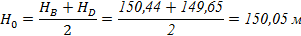
Определяем условное превышение между этими точками (B и D):
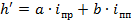
где 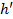 - условное превышение по диагонали BD,
- условное превышение по диагонали BD, 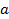 - длина здания (равна 36 м),
- длина здания (равна 36 м), 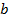 - ширина здания (равна 12 м),
- ширина здания (равна 12 м), 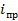 - продольный уклон (равен 0,01),
- продольный уклон (равен 0,01), 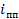 - поперечный уклон (0,01).
- поперечный уклон (0,01).

4). Вычислить красные (проектные) отметки углов здания.
Начинаем с более высокой отметки по диагонали BD:
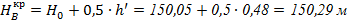
Затем переходим к противоположной точке диагонали

Отметку угла А определяем по найденной отметке  :
:
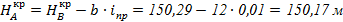
Отметку угла С находим по отметке  :
:
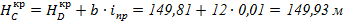
5). На плане в горизонталях в углах здания записываем над чертой красным цветом проектные отметки, под чертой – черные отметки (см. приложение 4).
Приложения к задаче 2:
1). Картограмма земляных работ – приложение 3.
2). План вертикальной привязки здания к строительной площадке – приложение 4.
|
из
5.00
|
Обсуждение в статье: Этапы решения задачи 1 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

