 |
Главная |
Алгоритм схемы Халецкого
|
из
5.00
|
· Вводим матрицу A и вектор f.
· Обнуляем вспомогательные матрицы B и C.
· Задаем первый столбец B и первую строку C по формулам (3.7) и (3.8).
· Вычисляем остальные элементы матриц B и C.
Þ Перебор строк (цикл i от 1 до N)
Þ Перебор столбцов (цикл j от 1 до N)
Þ Если  , то вычисляем
, то вычисляем  по формуле (3.7).
по формуле (3.7).
Þ Если 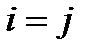 , положим
, положим  .
.
Þ Если  , то вычисляем
, то вычисляем  по формуле (3.8).
по формуле (3.8).
Þ Конец перебора строк и столбцов.
· Проверяем правильность вычисления матриц B и C. Для этого достаточно вычислить произведение  и сравнить с A.
и сравнить с A.
· Определим вектор y по формуле (3.9).
· Вычислим решение x по формуле (3.10).
· Выведем матрицу A и вектор правой части f, решение x и невязку Ax-f на экран.
Вычисление невязки решения
Для проверки правильности решения системы линейных алгебраических уравнений необходимо вычислить невязку решения. Невязка v является вектором и вычисляется по формуле
 , (3.11)
, (3.11)
где  - приближенное решение системы уравнений Ax=f.
- приближенное решение системы уравнений Ax=f.
Если решение  является точным решением, то невязка v будет равна нулевому вектору. При решении задачи на компьютере, точное решение получить практически невозможно из-за ошибок округления. Приближенное решение является приемлемым, если его невязка не будет превосходить заранее заданной погрешности Eps. Обычно погрешность Eps равна 0.001, но это значение можно изменять в зависимости от поставленной задачи и требуемой точности решения.
является точным решением, то невязка v будет равна нулевому вектору. При решении задачи на компьютере, точное решение получить практически невозможно из-за ошибок округления. Приближенное решение является приемлемым, если его невязка не будет превосходить заранее заданной погрешности Eps. Обычно погрешность Eps равна 0.001, но это значение можно изменять в зависимости от поставленной задачи и требуемой точности решения.
Итерационные методы
Итерационные методы основаны на построении итерационной последовательности  , сходящейся к искомому решению системы
, сходящейся к искомому решению системы  .
.
Каждый такой метод характеризуется своей итерационной формулой, позволяющей вычислять очередное приближение  по ранее найденным.
по ранее найденным.
В простейшем случае при вычислении  используется только одно приближение
используется только одно приближение  . Такие методы называют одношаговыми или двухслойными. Итерационную формулу для одношаговых методов принято записывать в стандартной канонической форме.
. Такие методы называют одношаговыми или двухслойными. Итерационную формулу для одношаговых методов принято записывать в стандартной канонической форме.
 . (3.12)
. (3.12)
где  - итерационный параметр (
- итерационный параметр (  >0),
>0),  - вспомогательная невырожденная матрица.
- вспомогательная невырожденная матрица.
Метод называется стационарным, если для 
 и
и 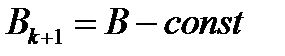 .
.
Стационарные методы - наиболее простые с точки зрения организации вычислительного процесса. Однако нестационарные методы имеют другие преимущества, связанные с выбором  и
и  для ускорения сходимости итерационного процесса.
для ускорения сходимости итерационного процесса.
Определение очередного приближения  с помощью итерационной процедуры (3.12) требует решения уравнения
с помощью итерационной процедуры (3.12) требует решения уравнения
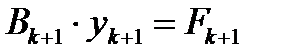 , (3.13)
, (3.13)
где
 .
.
Такую процедуру приходится выполнять на каждом шаге. Поэтому итерационный метод можно применять при условии, что определение отдельных членов итерационной последовательности  требует существенно меньшего объема вычислений, чем прямое решение исходной системы. Это накладывает ограничения на выбор матрицы
требует существенно меньшего объема вычислений, чем прямое решение исходной системы. Это накладывает ограничения на выбор матрицы  .
.
Самый простой случай, когда  . Тогда формула (3.13) приобретает вид
. Тогда формула (3.13) приобретает вид
 . (3.14)
. (3.14)
Итерационные методы, со схемой вычислений (3.14), называются явными.
Среди неявных методов (  ) наибольшее распространение получили методы с треугольной матрицей
) наибольшее распространение получили методы с треугольной матрицей  .
.
Разность между приближенным решением  и точным решением
и точным решением  называется погрешностью
называется погрешностью  .
.
Погрешность удовлетворяет итерационной формуле:
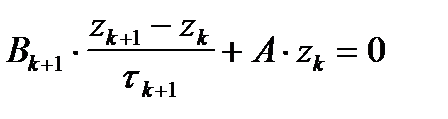 .
.
Итерационный процесс сходится  , если
, если  при
при  .
.
Матрица  называется транспонированной матрицей
называется транспонированной матрицей 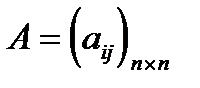 , что записывается
, что записывается  , если
, если  для всех
для всех  .
.
Матрица 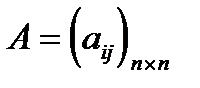 называется симметричной (
называется симметричной (  ), если
), если  для всех
для всех  .
.
Матрица 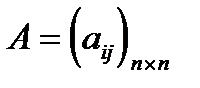 называется положительно определенной (
называется положительно определенной (  ), если для
), если для  имеем
имеем  .
.
Матрица 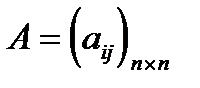 называется матрицей с диагональным преобладанием, если ее элементы удовлетворяют неравенству:
называется матрицей с диагональным преобладанием, если ее элементы удовлетворяют неравенству:
 для любого
для любого  .
.
Примеры:
 ,
, 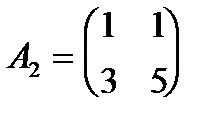 и
и 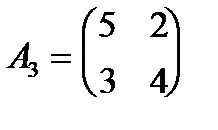 .
.
 - симметричная матрица,
- симметричная матрица, 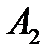 и
и  - несимметричные.
- несимметричные.
 - не положительно определенная, т.к. для
- не положительно определенная, т.к. для  имеем
имеем  .
.
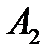 - положительно определенная, т.к. для
- положительно определенная, т.к. для  получаем
получаем  .
.
 и
и 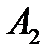 - без диагонального преобладания,
- без диагонального преобладания,  - с диагональным преобладанием.
- с диагональным преобладанием.
|
из
5.00
|
Обсуждение в статье: Алгоритм схемы Халецкого |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

