 |
Главная |
Операторы в геометрических пространствах
|
из
5.00
|
Задача 3.Найти матрицу проецирования пространства V3 на плоскость  параллельно оси
параллельно оси  .
.
Решение.Базисные векторы  переходят при проецировании в себя, вектор
переходят при проецировании в себя, вектор  переходит в
переходит в  (нулевой вектор). Матрица оператора имеет вид:
(нулевой вектор). Матрица оператора имеет вид:
 .
.
Задача 4.Найти матрицу поворотапространства V3 вокруг оси 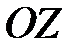 на угол
на угол  .
.

|
| j |
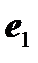
|

|

|
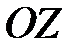 вектор
вектор 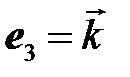 переходит в себя, а плоскость
переходит в себя, а плоскость  поворачивается на угол
поворачивается на угол  . Найдем координаты векторов
. Найдем координаты векторов  – образов базисных векторов
– образов базисных векторов 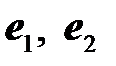 при повороте на угол
при повороте на угол 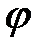 . Проекции вектора
. Проекции вектора  равны
равны  , а вектора
, а вектора  –
–  (см. рис.), то есть
(см. рис.), то есть  .
.
Следовательно, матрица  оператора поворотаплоскости
оператора поворотаплоскости  на угол j имеет вид:
на угол j имеет вид:  , а матрица оператора поворотапространства вокруг оси
, а матрица оператора поворотапространства вокруг оси  на угол j имеет следующий вид:
на угол j имеет следующий вид:
 .
.
Операторы в функциональных пространствах
Задача 5.Выбрав подходящий базис в пространстве  многочленов степени не выше
многочленов степени не выше  , найти матрицу
, найти матрицу 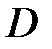 оператора дифференцирования
оператора дифференцирования  в этом базисе.
в этом базисе.
Решение. Выберем в  базис
базис  . Т.к.
. Т.к.  , то матрица
, то матрица  оператора дифференцирования в этом базисе имеет вид:
оператора дифференцирования в этом базисе имеет вид:
 (мы ограничились, для простоты, случаем
(мы ограничились, для простоты, случаем  ).
).
Задача 6.Выбрав подходящий базис в функциональном пространстве 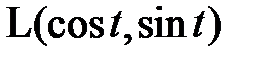 , найти матрицу оператора
, найти матрицу оператора  сдвига аргумента на
сдвига аргумента на 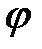 в этом базисе
в этом базисе  .
.
Решение.Выберем в  базис
базис 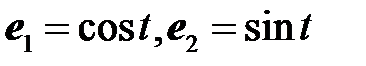 . Применим оператор
. Применим оператор  к базисным векторам (функциям). Получим:
к базисным векторам (функциям). Получим:

Следовательно, матрица  оператора сдвига аргумента в пространстве
оператора сдвига аргумента в пространстве  в базисе
в базисе  имеет следующий вид:
имеет следующий вид:  .
.
Матричная запись действия оператора
Задача 7.Заданы матрица  оператора
оператора  и координаты
и координаты  вектора
вектора  . Найти координаты
. Найти координаты  вектора
вектора  .
.
Решение.Координаты  вектора
вектора  определяются с помощью умножения матрицы
определяются с помощью умножения матрицы  оператора
оператора  на столбец
на столбец  из координат вектора
из координат вектора  , то есть
, то есть  .
.
 .
.
З а д а ч и д л я с а м о с т о я т е л ь н о г о р е ш е н и я
1.Выяснить, какие из заданных преобразований  являются линейными и найти их матрицы.
являются линейными и найти их матрицы.
1)  ; 2)
; 2) 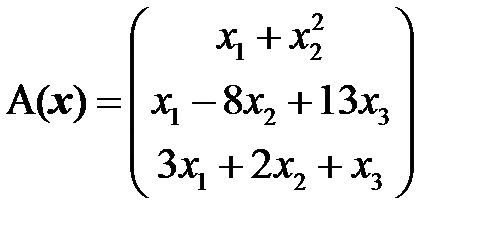 ;
;
3)  ; 4)
; 4)  .
.
2.Найти матрицы линейных преобразований пространства 
1) Проецирования пространства на ось  параллельно плоскости
параллельно плоскости  .
.
2) Симметрии пространства относительно плоскости  .
.
3) Симметрии пространства относительно оси  .
.
4) Поворотпространства вокруг прямой  на угол 120°.
на угол 120°.
3. Выбрав подходящие базисы в функциональных пространствах, найти матрицы указанных линейных операторов.
1) Оператора дифференцирования на пространстве  .
.
2) Оператора сдвига аргумента  на пространстве
на пространстве  .
.
3) Оператора дифференцирования на пространстве  .
.
4) Оператора сдвига аргумента  на пространстве
на пространстве  .
.
4. Заданы координаты  вектора
вектора  и матрица
и матрица  оператора
оператора  . Найти координаты
. Найти координаты  вектора
вектора 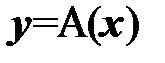
1)  ;
; 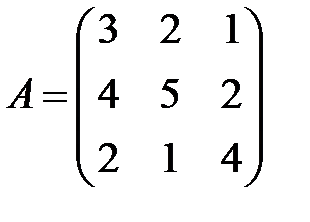 ; 2)
; 2)  ;
;  ;
;
3) 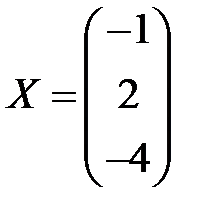 ;
;  ; 4)
; 4) 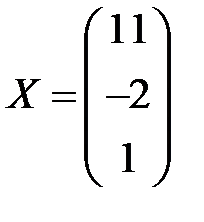 ;
; 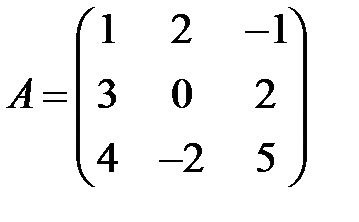 .
.
Ответы:
1.1)  ; 3)
; 3)  .
.
В задачах2) и 3) преобразования  не являются линейными.
не являются линейными.
2.1)  2)
2)  3)
3)  4)
4)  .
.
3.1) 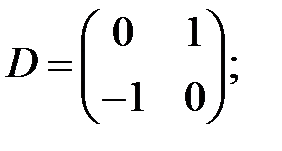
2)  3)
3)  4)
4)  .
.
4.1) 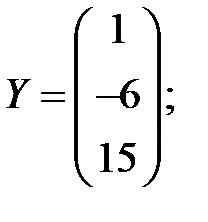 2)
2)  3)
3) 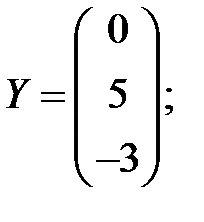 4)
4)  .
.
Тема 5. Определители
|
из
5.00
|
Обсуждение в статье: Операторы в геометрических пространствах |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

