Построение многогранников

 

 

Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником. К наиболее часто используемым в практике многогранникам относятся призма и пирамида.

Чертёж любого многогранника состоит из сочетания многоугольников. Каждая линия на чертеже многоугольника - это либо проекция линии пересечения двух граней (ребра), либо проекция самой грани (плоскости), если эта грань перпендикулярна плоскости проекций. При проецировании многогранника на плоскость чертежа необходимо уметь мысленно разделять его на составные части и правильно определять порядок их изображения.

Вспомним из курса черчения, как изображаются на чертеже плоские фигуры, различно расположенные относительно плоскостей проекций:

- плоская фигура, параллельная плоскости, проецируется на неё без искажения;

- плоская фигура, перпендикулярная к плоскости, проецируется на неё в прямую линию;

- плоская фигура, наклонённая к плоскости, проецируется на неё с искажением.

Плоскости, наклонённые к плоскостям проекций, называются плоскостями общего положения. Рассмотрим построение многоугольников в случае, когда они являются плоскостями общего положения.

Проекцией треугольника в общем случае является треугольник. Чтобы построить на чертеже проекции треугольника, необходимо построить проекции его вершин (точек). Следует помнить, что они должны лежать на одной линии связи. Проекцией четырёхугольника в общем случае будет четырёхугольник. При этом у квадрата, прямоугольника, ромба и параллелограмма сохраняется параллельность противоположных сторон (проекции параллельных прямых - параллельны).

На чертеже четырёхугольника произвольно можно построить только одну его проекцию и три вершины на другой проекции (три точки определяют плоскость). Проекцию четвёртой вершины нужно строить исходя из принадлежности её плоскости четырёхугольника (найти её на одной из диагоналей) (рис. 3.6).

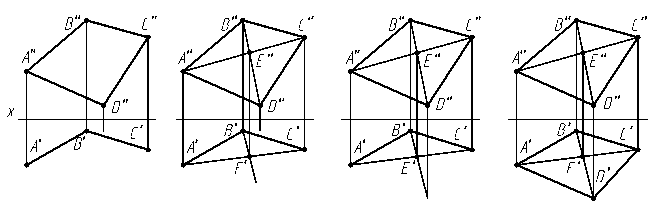
а) б) в) г)

Рис. 3.6

 

Аксонометрические проекции многогранников, так же как и многоугольников, строятся при помощи координат вершин многогранника.

Рис. 22

Построение геометрического тела в аксонометрии начинается с построения плоской геометрической фигуры - многоугольника. При построении правильного шестиугольника в изометрии или диметрии центровые линии заданной фигуры принимаются за координатные оси (рис. 3.7), относительно которых ориентируются вершины рассматриваемой фигуры. Например, координата вершины 1 определяется радиусом R; вершины 6- отрезками R/2 и hдля изометрии (рис. 3.7б) и отрезками R/2 и h/2для диметрии (рис. 3.7в).

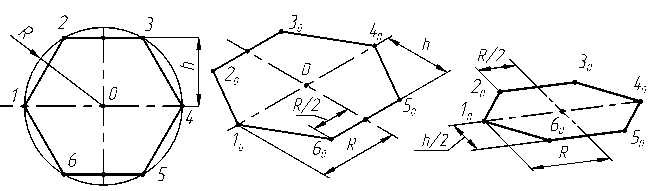
а) б) в)

Рис. 3.7

 

Построим прямоугольную изометрию правильной шестиугольной пирамиды. На свободном месте поля строят основание (рис. 3.7б), из точки пересечения осей проводят отрезок прямой, равный высоте пирамиды (рис. 3.8). Вершину пирамиды соединяют прямыми линиями с вершинами шестиугольного основания.

Построение прямой шестигранной призмы в диметрии (рис. 3.9) также начинают с построения нижнего основания (рис 3.7в). Затем из каждой вершины нижнего основания проводят вертикальные прямые, на которых откладывают высоту призмы. Полученные точки соединяют отрезками и получают верхнее основание.

Рис. 3.8 Рис. 3.9

Построение наклонной призмы в аксонометрии начинают с проведения аксонометрических осей и построения нижнего основания. Затем строят одно ребро боковой грани, для чего по координатам определяют верхнюю точку ребра (рис. 3.10). После этого можно построить верхнее основание и провести остальные рёбра боковых граней.

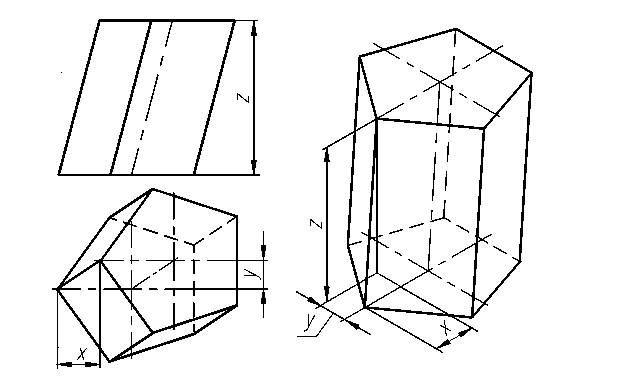
Рис. 3.10

 

Построение проекций точек, лежащих на поверхности многогранника. При выполнении заданий по проекционному черчению приходится строить линию пересечения двух поверхностей. Для этого необходимо уметь находить точки, расположенные на поверхности геометрических тел.

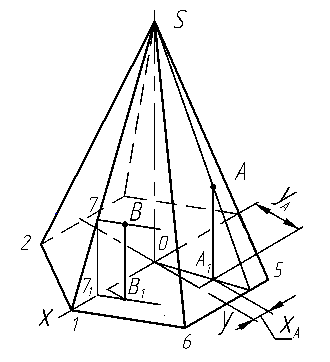
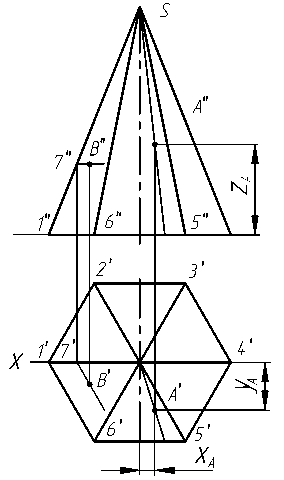На чертеже для построения горизонтальной проекции точки А, расположенной на поверхности пирамиды, через заданную проекцию точки А″ проводят прямую линию и находят её горизонтальную проекцию (рис. 3.11а). На горизонтальной проекции прямой с помощью линии связи находят горизонтальную проекцию А′ точки А. При построении точки А в изометрической проекции необходимо сначала построить на основании пирамиды её проекцию А₁, определяемую координатами X_A и Y_A (рис. 3.11б). Затем через построенную точку А₁ нужно провести линию параллельно вертикальной оси и отложить на ней координату Z_A . Полученная точка А и будет изображением точки А в изометрии. Аксонометрическое изображение является обратимым изображением, что подтверждается возможностью построения аксонометрической координатной ломаной любой точки поверхности, принадлежащей пирамиде.

а) б)

Рис. 3.11

Координатными ломаными пользуются, если нельзя применить какой-либо частный приём. Например, по наглядному изображению точки В(рис. 3.11б), принадлежащей боковой грани пирамиды, можно определить координаты точки и построить её горизонтальную и фронтальную проекции. Для этого через точку В проводим прямую линию, параллельную ребру 1 6, до пересечения с ребром S 1 и получаем точку 7, лежащую в координатной плоскости хОу. Строим проекцию точки 7 на основании пирамиды (точку 7₁) и проводим отрезок прямой параллельно 1 6, на котором определяем точку В₁ .

По координатам точки В, определённым на аксонометрической проекции (рис. 3.11б), можно построить горизонтальную и фронтальную проекции точки В на чертеже (рис. 3.11а).

 

 

Тела вращения

 

 

Цилиндр - геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями. Цилиндрическая поверхность вращения образуется при вращении прямой линии g (образующей) вокруг оси i, параллельной образующей (рис. 3.12 а). Если часть цилиндрической поверхности отсечь двумя плоскостями, перпендикулярными к оси вращения, то ограниченное этими плоскостями и цилиндрической поверхностью тело будет являться прямым круговым цилиндром.

а) б) в)

Рис. 3.12

Отметим на прямой g ряд точек, при вращении каждая точка опишет окружность (параллель). Если на этом цилиндре отметить ряд промежуточных меридианов, то можно получить изображение цилиндра с каркасом, нанесённым на его поверхность (рис. 3.12б).

На рис. 3.12в представлены три проекции прямого кругового цилиндра, ось вращения которого перпендикулярна горизонтальной плоскости. Проводим фронтальную проекцию образующей цилиндра через A″. Она является горизонтально-проецирующей прямой и проецируется в точку на окружности. В этой точке будет находиться и горизонтальная проекция A′ точки A , так как точка видна относительно фронтальной плоскости проекций. Профильная проекция точки A находится в проекционной связи с проекциями A′ и A″. Чтобы найти профильную проекцию A″′, надо провести линию связи из точки A″ и отложить расстояние y от оси z. Все три проекции точки видимы.

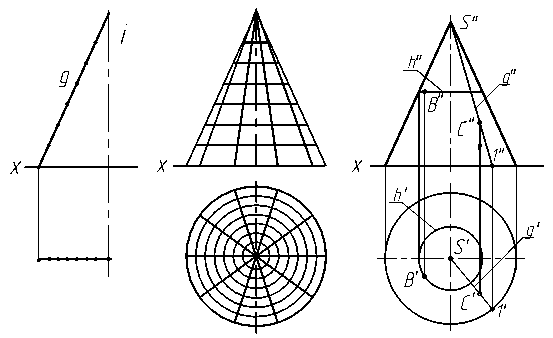
Конус - геометрическое тело, ограниченное конической поверхностью и плоскостью. Коническая поверхность образуется вращением прямой g вокруг оси i, которая пересекает эту прямую (рис. 3.13а). Точка S пересечения образующей и оси вращения называется вершиной конической поверхности.

а) б) в)

Рис. 3.13

 

Отметим на прямой g ряд точек, при вращении каждая из них опишет окружность (параллель). Если на этом конусе отметить ряд промежуточных меридианов, то можно получить изображение конуса с каркасом, нанесённым на его поверхность (рис. 3.13б).

На рис. 3.13в представлены две проекции прямого кругового конуса, ось вращения которого перпендикулярна горизонтальной плоскости проекций. На поверхности задана проекция точки A″. Проводим фронтальную проекцию образующей конуса через A″ и S″ - S″1″. Находим горизонтальную проекцию образующей S′1′, используя линии связи и принадлежность точки 1 окружности основания конуса. Горизонтальная проекция точки A′ находится на пересечении линии связи с горизонтальной проекцией образующей S′1′. Чтобы найти горизонтальную проекцию точки В по заданной В″, проведём через неё параллель h″ и построим h′, которая проецируется на горизонтальную плоскость проекций в окружность. Горизонтальная проекция точки В′ находится на пересечении линии связи с горизонтальной проекцией h′.

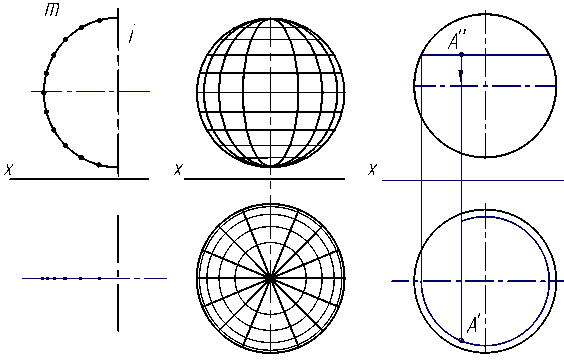
Шар - геометрическое тело, ограниченное сферической поверхностью. Сферическая поверхность образуется вращением дуги окружности m вокруг диаметра i (рис. 3.14а). Отметим на дуге m ряд точек, при вращении дуги каждая точка опишет окружность (параллель). Если на этой сфере отметить ряд промежуточных меридианов, то можно получить изображение шара с каркасом, нанесённым на его поверхность (рис. 3.14б).

а) б) в)

Рис. 3.14

Рассмотрим нахождение горизонтальной проекции точки А, принадлежащей сфере, по заданной её фронтальной проекции А'' (рис. 3.14в). Через фронтальную проекцию точки А'' проведём параллель (линия, параллельная горизонтальной плоскости). От точки пересечения параллели и окружности главного меридиана проведём линию связи до горизонтальной проекции главного меридиана (горизонтальная осевая линия). Через найденную точку проведём окружность (горизонтальная проекция параллели). От фронтальной проекции точки проведём линию связи, которая пересечёт окружность в двух точках. Поскольку А'' видима, то выбираем точку с большей координатой y и обозначаем А'.

Аксонометрические проекции тел вращения. Основанием ряда геометрических тел вращения является окружность. Чтобы построить геометрическое тело в аксонометрии, надо уметь строить, прежде всего, его основание. Изображения окружностей в изометрии и диметрии во всех трёх плоскостях проекций представляют собой эллипсы. В практике выполнения аксонометрических чертежей допускается сложные лекальные построения эллипсов заменять более простыми построениями овалов, вычерчиваемых при помощи циркуля.

Построим изометрическую проекцию окружности радиуса R, расположенной в горизонтальной плоскости, заменив эллипс четырехцентровым овалом (рис. 3.15).

Рис. 3.15

Малая ось эллипса (0₁ 0₁) параллельна оси, отсутствующей в горизонтальной плоскости, т.е. оси z (рис. 3.15). Большая ось перпендикулярна малой. Необходимо также провести аксонометрические оси х, у и вспомогательную окружность радиуса R. Построенный овал должен проходить через точки 1, так как только в этом случае сохранятся размеры вдоль координатных осей.

Центры большой дуги овала (0₁) находятся на пересечении вспомогательной окружности с продолжением малой оси (рис. 3.15). Радиус большой дуги R₁ равен расстоянию от 0₁ до точки 1. Точки пересечения отрезков 0₁1 с большой осью будут центрами 0₂меньших дуг овала. Отрезок 0₂1 равен радиусу меньшей дуги. Проведя теперь меньшие дуги овала, получим четырехцентровой овал.

В прямоугольной диметрии, так же как и в изометрии, малая ось эллипса параллельна той аксонометрической оси, которая перпендикулярна плоскости проекций, где расположена изображаемая окружность.

Рис. 3.16

Рассмотрим построение в плоскости х0z овала радиусом R (рис. 3.16). Из точки пересечения осей хиz проводим окружность радиуса Rи на пересечении с осями получаем точки 1,которые являются точками касания дуг овала. Затем строим центры дуг, для чего из точек 1, принадлежащих оси х, проводим горизонтальные прямые до пересечения с большой и малой осями эллипса и получаем точки 0₁ и 0₂. Точки 0₁, лежащие на малой оси, являются центрами больших дуг овала, а точки 0₂ - центрами малых дуг. Из центров 0₁ радиусом R₁, равным отрезку 0₁1, проводим большие дуги овала, а из центров 0₂ - малые дуги овала.

Рис. 3.17

На рис. 3.17 приведено построение овала в плоскости х0у. На оси х строим точки 1 касания дуг овала. Для нахождения центров 0₁ больших дуг овала от пересечения осей хиувверх и вниз по направлению малой оси откладываем отрезки, равные 2R. Центры малых дуг овала 0₂ находим на пересечении отрезка 0₁1 и большой оси эллипса. Большие дуги овала проводим из центров 0₁ через точки 1, малые дуги - из центров 0₂.

Построение аксонометрической проекции поверхности вращения (конуса, цилиндра) начинают с построения кругового основания. Затем на вертикальной оси откладывают высоту. Для цилиндра (рис. 3.18) строят верхнее основание и проводят очерковые образующие - касательные к двум овалам оснований. У конуса вершину S соединяют касательными с основанием (рис. 3.19).

Для построения точки А на поверхности цилиндра в прямоугольной изометрии сначала строят проекцию точки А₁ на основании цилиндра по координате Х_А , взятой с горизонтальной проекции (рис. 3.12в). От точки А₁ параллельно оси 0z проводят прямую и откладывают координату Z_А, взятую с фронтальной проекции (рис. 3.12в).

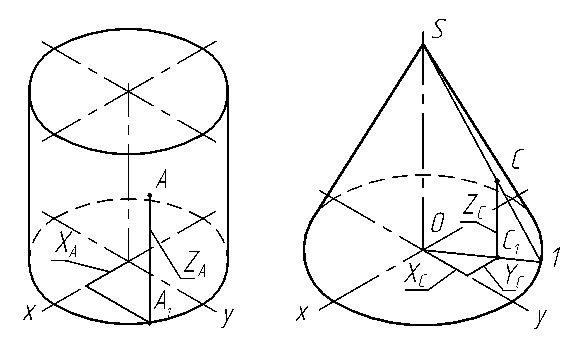
Рис. 3.18 Рис. 3.19

 

Построение точки С на поверхности конуса в изометрии (рис. 3.19) выполняют в следующей последовательности: строят проекцию точки С₁ на основании конуса по координатам X_А и Y_А , взятым с горизонтальной проекции (рис. 3.13в), от точки С₁ параллельно оси 0z проводят прямую и откладывают координату Z_С, взятую с фронтальной проекции (рис. 3.13в).

Если же по наглядному изображению точки Стребуется определить её координаты, то вначале через заданную точку С проводят образующую S1 и строят её проекцию 01 на основание конуса, а затем из точки С проводят прямую, параллельную оси 0z, и строят точку С₁. Выполненные построения позволяют определить координаты точки С на наглядном изображении.