Форма и размеры Земли – геоид, общеземной эллипсоид,земн.шар

Предмет и задачи инженерной геодезии

Геодезия - наука, изучающая форму и размеры Земли, геодезические приборы, способы измерений и изображений земной поверхности на планах, картах, профилях и цифровых моделях местности. В процессе развитии геодез. в ней выделились ряд связанных между собой научных дисциплин. Назовём те которые нужн учитывать или исп. в геодезич. обеспечении строительства:

- высшая геодезия ( изучает методы определения формы и размеров Земли)

- топография и гидрография развивают методы съемки участков земной поверхности и изображения их на плоскости в виде карт, планов и профилей;

- фотограмметрия занимается обработкой фото-, аэрофото- и космических снимков для составления карт и планов;

- картография- изучает теоретические основы картографических проекций и технологию созд. карт различн. масштабов;

- маркшейдерия - область геодезии, обслуживающая горнодобывающую промышленность и строительство тоннелей;

- инженерная (прикладная) геодезия изучает методы геодезических работ, выполняемых при изысканиях, проектировании, строительстве и эксплуатации различных зданий и сооружений.

-космическая(спутниковая геодез.)-рассматривает методы координатн.описаний движения искуств. спутников земли в режиме реального времени.

Задачи инженерной геодезии:

1) топографо-геодезические изыскания различных участков, площадок и трасс с целью составления планов и профилей;

2) инженерно-геодезическое проектирование - преобразование рельефа местности для инженерных целей, подготовка геодезических данных для строительных работ;

3)Геодезические разбивочные работы:- вынос проекта в натуру, детальная разбивка осей зданий и сооружений;

4) геодез.выверка конструкций и технологического оборудования при установке их в проектное положение,

5) наблюдения за деформациями зданий и сооружений.

При топографо-геодезических изысканиях выполняют:

а) измерение углов и расстояний на местности с помощью геодезических приборов (теодолитов, нивелиров, лент, рулеток и др.);

б) вычислительную (камеральную) обработку результатов полевых измерений на ЭВМ;

в) графические построения планов, профилей, цифровых моделей местности (ЦММ).

 

Исторические сведения о развитии геодезии.

Геодезия – возникла в древности. Она возникла и развивалась исходя из практических запросов человека(необходимость ориентирования на местности, межевание земель, определение площади участк,

при строительстве сооружений, определен.форм,выполн. измерен.на местности, по их результатам задавали уклоны водотоков,составл.чертежи участков земн.поверхн. и сооружений на ней.

В дренв.Египте, Греции 4 век до н.э исп. Различные тех.средства:отвесы, угольники, водн.уровни, угломерн.устройств и так стала формироватс геометрия (ЗЕМЛЕИЗМЕРЕНИЕ).В дальнейшем геометрия и геодезия получили свои теоритич. и практич. задачи. Основные теоремы, кот.формировали основы геометрии-Пифагоров треугольник служил для построен. угла на метсности, а число «пи» для расчёта R окружности.

В это ж время создвались простейшие приборы: мерные шнуры, отвесы,угольники,водн.уровни). Голандский учёный Снелиус предложил определять большие расст. методом Триангуляции. К 1795г. во Франции была установлена единица измерения длины – метр(раная 1/40.000000 длины дуги Парижского меридиана.Первые теоретич.работы на тер.РБ проведены были в 1816-1821 корпусом воен.фотограф.В России в Виленск.губерни была созд. Первая сеть триангуляции. В 1969 году на смену оптико механич.-приборам стали внедрять электрон.цифровые измерит.комплексы и компьютерные технологии.

Форма и размеры Земли – геоид, общеземной эллипсоид,земн.шар.

Реальная поверхность земной коры представляет собой рельеф с сочетанием

неровностей различной величины и формы. Фигура земли формируется под действием сил внутреннего тяготения и центробежной силы. Принято считать что земля имеет две поверхности: физическую- образованную твердой оболочкой земли и уровневую поверхность (Мировой океан(70%)) мысленно продолженную под сушей.(геоід)

Геоид – гладкая всюду выпуклая поверхность,образован.уровнем воды мирового океана в состоянии полного покоя и ранвовесия мыслено продолженая под материками и к каждой её точки вектор силы тяжести явл.нормалью к ней. Сущ.различные системы высот. В РБ принята Балтийская система высот за отсчётную поверхность которой принята поверхность геоида,проходящая через нуль Крондштадского футштока. Из-за неравномерного распределения плотности в земной коре и рельефа поверхность геоида имеет

глобальные и локальные волны и не имеет строгого геометри­

ческого описания, поэтому невозможно решение на ней задач

вычисления и передачи координат точек земной поверхности.

Для решения этих задач в геодезии используют математиче­

скую модель - общий земной эллипсоид, представленный эл­

липсоидом вращения, сжатым у полюсов, ось вращения кото­

рого и геометрический центр совпадают с осью вращения и

центром масс Земли. Системы геодезич.координат((широт ф, долгот А.), отнесённые к пов-ти эллипсоида назыв. общеземными геоцентрическими.Под руководством Красовского были получены параметры общего земного элипсоида(а=6378245, в=6356263, £=1/298,3 полярное сжатие). На его -(референц-элипсоид) поверхность проецировали центры геодезическ.пунктов полигонов триангуляции 1-ого класса и таким образом на поверхн эл. Была закреплена сис-ма координат СК-42, кот. до настоящего времени исп. на терр. РБ. Сейчас на поверхности эллипсоида была закреплена сис-ма геодезич.координат СК-95.К настоящему времени получены современные общеземные геоцентрические сис-мы координат. Примерами таких систем служат WGS-84(США), ПЗ-90 (Россия).

Во многих практических маркшейдерско-геодезических рас­

четах общий земной эллипсоид и референц-эллипсоид заме­

няются их более простой моделью - земным шаром радиуса

R = 6371 км (объем земного шара равен объему земного эл­

липсоида). Длина экватора L на эллипсоиде Ф.Н. Красовского

равна 2па, или 40 075 км, на земном шаре 2kR, или 40 000 км).

 

4. Метод проекции в геодезии: ортогональная проекция объектов земной поверхности на сферу, на плоскость, размеры площадок, которые можно считать плоскими прив в плане, учет кривизны Земли при определении превышений.}

Метод ортогональной проекции на горизонтальную плоскость. Иначе методо горизонтальной проекции, применяется при выполнении геодезических работ для отображения их данных на горизонтальной плоскости в виде числовых величин и картографических чертежей. Точки контура АВСМ земной поверхности (рис. 1.3, а) проецируют на уровенную поверхность Ру отвесными линиями. На уровенной поверхности точки а', Ь', с', m'; линии m'а', m'с; а'Ь', ..., а также контур db’c'm` представляют отвесные проекции соответствующих элементов контура АВСМ. Для ограниченной территории на горизонтальной плоскости Рт оргого-

 

нальная проекция осуществляется практически параллельными вертикальными лучами: получаются точки а, Ь, с, m; линии mа, mс, аЬ, а также контур abcm. В инженерной практике гори­

зонтальную плоскость Рт приближают к уровенной поверхности на территории города, промышленного предприятия. Отрезок прямой линии МА длиной D (см. рис. 1.3, а) принадлежит вертикальной плоскости m'МАа'. Угол наклона прямого отрезка МА измеряется относительно горизонтальной плоскости или параллельной ей прямой линии МА' (рис. 1.3, б). Длина d проекции та отрезка МА на горизонтальную плоскость называется горизонтальным проложением наклонной прямой линии и вычисляется по формуле d= D cosv(ню). (1.4)

Горизонтальные углы. В соответствии с методом ортогональной проекции на горизонтальную плоскость (горизонтальной проекции) в геодезии измеряют горизонтальный угол между направлениями МА и МС (см. рис. 1.3, а), который определяется как двугранный угол р между вертикальными плоскостями АМт'а' и СМт'с', проходящими через общую отвесную

линию Мт’ и заданные точки местности А и С. Поскольку горизонтальная плоскость РТ и уровенная поверхность Ру в точках m u m ' перпендикулярны отвесной линии Mmm', то гори­

зонтальный угол β будет одинаков на малых площадках уровенной поверхности и горизонтальной плоскости.Площади. Исходя из формулы (1.4), можно рассчитать, на ка­

кую величину преуменьшена площадь наклонного участка земной поверхности в проекции на горизонтальную поверхность.

Учет кривизны земной поверхности в инженерно-геодезических работах. Фактор кривизны Земли учитывается при картографировании ее поверхности и в ряде инженерно геодезических задач, например при измерении высот точек и расчете размеров участков на сфере, которые на практике можно принимать плоскими. При рассмотрении фактора кривизны используем шаровую модель Земли.

Учет кривизны Земли при измерении высот. Пусть точки Tо и Со - вертикальные проекции точек T и С поверхности Земли на сферу по радиусам R = ТО и R = СО рис. 1.2, а).

В точке To проведем горизонтальную линию T_oC₁ - касательную к сфере. Точка C₁ представляет вертикальную проекцию точки С на касательную T_oС₁, а вертикальное расстояние C_oC₁ = Δh выражает влияние фактора кривизны на измерения высот точек, определяемых относительно горизонтальных линий:

или

Для различных расстояний d при R = 6371 км по формуле (1.1) вычислим значения ДА и получим следующие результаты

(табл. 1.1).

Величина 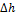учитывается как поправка при расчете высоты точки С₁ относительно поверхности G сферы или практически относительно основной уровенной поверхности Go- Не­совпадение между уровенной поверхностью G_o и горизонтальной плоскостью T₀C₁ необходимо учитывать при строительстве ряда сооружений, например тоннелей (рис. 1.2, б). Если тоннель проектировать в вертикальном разрезе прямолинейным по оси М₁Т₁, то после его строительства подземные и дождевые воды будут стекать относительно уровенной поверхности GG₁ (и отвесных линий) к средней его зоне N . Для обеспечения естественного стока тоннели строят с подъемом их средней части, например по профилю МВТ. Учет фактора кривизны Земли при измерении расстояний. Согласно рис. 1.2, а расстояния d и s между проекциями точек T и С на плоскость (точки T₀ и С₁) и на сферу (точки T₀ и С₁) различаются за счет фактора кривизны Земли на абсолютную величину

где угол = s /R и выражен в радианах. Значение d вычисляется и по приближенной формуле

(1.2)

Относительная величина Ad I d разности длин d и s получается из формулы (1.2):

(1.3)

Из формулы (1.3) рассчитываются на сферической поверхности размеры участка, в пределах которого можно не учитывать влияние фактора кривизны при условии, что допускается относительная величина искажения длины d / d - = 1 /1 ООО ООО (1 мм / 1 км). Решив уравнение (1.3), получаем d - 11 км - радиус участка, который отвечает поставленному

условию. Если принять иную величину допуска, например d / d = 1 / 200 ООО (5 мм /1 км), то плоским можн считать участок на сферической и уровенной поверхности радиусом 25 км.

 

5. Системы координат, применяемые в геодезии(глобальные, зональные в проекции Гаусса-Крюгера, местные).

Глобальные координаты

Для решения геодезических задач в глобальном масштабе используются различные системы глобальных(общеземных) координат: Географические, геодезические, астрономические, пространственные, прямоугольные.

 

Географические координаты используются когда нет необходимости учитывать сжатие земного элипсойда, что допустима для создания карт мелких масштабов. Положение точек земной поверхности в проекции на поверхность земного шара определ. угловыми величинами относительно исходных плоскостей.

Плоскости экватора и плоскости гринвичского меридиана.

Плоскость экватора проходит через центр элипсойда перпендикулярна его оси вращения PP₁ . Экватор представляет окружность – линию пересечения поверхности земного шара с плоскостью экватора.

Географическая параллель см. MN явл. окружн.,кот. образуется при пересечении земного шара плоскостью параллельно плоскости экватора.

Географическая широта угол между нормалью к поверхности земного шара и плоскости экватора. Широты отсчитываются от экватора к северному полюсу – со знаком + и к югу со знаком - . широта экватора равна 0, а севера + 90^о

Географическая долгота - двухгранный угол между плоскостью географического меридиана в точке N и плоскостью Гринвичского меридиана для отсчета долгот. Долготы отсчитываются на восток от 0^о до 360^о или же на восток от 0 до 180^о с указанием « восточная долгота» или на запад от 0 до – 180^о с указанием «западная долгота».

Астрономические определяю путём наблюдения звезд при помощи астрономических приборов с использованием радиосигналов точного времени.

Геодезические координаты близки географически но отличия в то что они отсчитываются по нормалям к поверхности референц-эллипсоида.

Системы геоцентрических пространственных прямоугольных координат применяются в спутниковых системах позиционирования. Это вызвано тем,что координато несущие точки являются созвездиями специальныз искусственных спутников Земли, которые обращаются по орбитам вокруг центра масс Земли на высотах приблизительно 20т. Км. Всемирная геоцентрическая система координат WGS – 84 (США) поддерживается созвездием GPS-NAVSTAR рекомендовано к практическому применению международным союзом геодезии и геофизики.

Пространственные прямоугольные координаты в точке N определены отностильно центра масс земли m и координатных осей X,Y,Z (см.рис 1.4)

Геоцентрическая система ПЗ-90 (параметры земли) РФ, поддерживается созвездием ГЛОНАСС является аналогом системы WGS-84(см.рис 1.4)