Тема 2.3 Исследование функции методами дифференциального исчисления

2015-11-10

1172

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒

2.31 Исследование функций на возрастание и убывание

Теорема (достаточное условие возрастания функции) Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Теорема (достаточное условие убывания функции) Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

у у

0 х₁х₂0 х₁х₂

а) Рис.1 b)

Если касательные к кривой в некотором промежутке направлены под острыми углами к оси абсцисс(рис.1.а), то функция возрастает, если под тупыми (рис. 1.b), то убывает.

Пример . Найти промежутки монотонности функции

у= x²-4x+3.

Решение :

у^/=2х-4.

y^/>0 при 2х-4>0 ; y^/<0 при 2x-4<0;

2x>4 ; 2x<4;

x>2 . x<2.

Получаем, что функция возрастает на (2;+∞), а убывает на (-∞;2).

2.32 Исследование функции на экстремум.

Определение 1.Точка х₀ называется точкой максимума функции f(x), если в некоторой окрестности точки х₀выполняется неравенство f(x) ≤ f(x₀).

Значения функции в точках х₀ и х₁называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием

Определение 2.Точка х₀ называется точкой минимума функции f(x), если в некоторой окрестности точки х₀выполняется неравенство f(x) ≥ f(x₁).

f(x₀)

f(x₂)

f(x₁)

0 х₀х₁х₂х

Рис.2

названием экстремума функции. Экстремум функции часто называют локальным экстремумом.

В точках локального экстремума дифференцируемой функции ее производная равна нулю.

Поэтому необходимое условие экстремума может быть сформулировано следующим образом.

Для того, чтобы функция у= f(x)имела экстремум в точке х₀, необходимо, чтобы ее производная в этой точке равнялась нулю

( f ^/ (х)=0) или не существовала.

Точки, в которых производная равна нулю или не существует, называются критическими.

Таким образом, если в какой- либо точке имеется экстремум, то эта точка критическая. Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.

Схема исследования функции у= f(x) на экстремум.

1⁰. Найти производную у^/= f ^/(x).

2⁰. Найти критические точки функции, в которых производная

f ^/(x) =0 или не существует.

3⁰. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.

4⁰. Найти экстремумы ( экстремальные значения) функции.

Пример . Исследовать на экстремум функцию

у=х(х-1)³.

Решение :

1) Производная. у^/=1^.(х-1)³+3х^.(х-1)²=(х-1)^2.(х-1+3х)=(х-1)^2.(4х-1).

2) Приравнивая производную к нулю, находим критические точки функции: (х-1)^2.(4х-1)=0

(х-1)²=0 или 4х-1=0

х-1=0 4х=1

х₁=0 х₂= .

3) Нанесем критические точки на числовую прямую.

у^/

+ + х

у 1

Для определения знака производной слева и справа от критической точки х= выберем, например, значения х=0 и х=0,5 и найдем f^/(0)=-1 <0 и f^/(0.5)= >0; следовательно, f^/(x)<0 при всех х< и f^/(х)>0 на интервале ( ;1).

Аналогично устанавливаем, что f^/(x)>0 и на интервале (1;∞).

Согласно условию х= - точка минимума. В точке х=1 экстремума нет.

4) Находим значение функции f_min( )= ( -1)³=- .

2.33 Наибольшее и наименьшее значения функции на отрезке.

Если функция у=f(x) непрерывна на отрезке [a;b], то она принимает на нем наибольшее и наименьшее значения. Наименьшее и наибольшее значение функции может достигаться как в точках экстремума так и в точках на концах отрезка. Так, на рисунке, наибольшее значение функции на конце отрезка х=b, а наименьшее- в точке минимума х₁.

y

Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой: 1⁰. Найти производную f ^/(x). 2⁰. Найти критические точки функции, в которых производная равна нулю или не существует. 3⁰. Найти значения функции в критических точках и на концах

0 a x₁ b x

Рис.3

отрезка и выбрать из них наибольшее f_max и наименьшее f_min.

Пример: Найти наибольшее и наименьшее значения функции

у=(х-2)^2.е^-х на отрезке [0;5].

Решение :

1⁰. f^/(x) = 2(x-2)^.e^-^x-(x-2)^2.e^-^x= -e^-^x.(x-2)(x-2-2)=-e^-^x.(x-2)(x-4).

2⁰. f^/(x) =0, -e^-^x.(x-2)(x-4)=0

-e^-^x=0 или х-2=0 или х-4=0

нет решения х₁=2 х₂=4

3⁰. значения функции в критических точках f(2)=0, f(4)= и на концах отрезка f(0)=4 и f(5)= . Итак, f_max=f(0)=4, f_min(2)=0.

2.34. Исследование функции на выпуклость, вогнутость и точки перегиба.

Нахождение экстремумов во многом определяет структуру графика функции. Определим теперь другие « узловые» точки функции, которые также следует найти, чтобы качественно построить график.

у у у

0 х₁х₂х₃х₄ х₅ х 0 х 0 х

а) б) в)

Рис.4

рассмотрим функцию, график которой изображен на рис.4а. эта функция возрастает на всей числовой оси и не имеет экстремумов. Очевидно, однако , ее отличие от функций, изображенных на рис. 4б и 4в. В точках х₁, х_2, х₃, х₄, х₅ график как бы «перегибается». Поэтому такие точки называются точками перегиба, к строгому определению которых мы переходим.

Прежде всего определим различие поведения функции по разные стороны от точек х₁, х_2, х₃, х₄, х_5.

Определение 1.Функция называется вогнутой на промежутке Х, если для любых двух значений х₁, х₂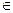Х из этого промежутка выполняется неравенство

График вогнутой функции расположен над касательной в окрестности точки касания рис. 5а.

Определение 2. Функция называется выпуклой на промежутке Х, если для любых двух значений х₁, х₂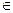Х из этого промежутка выполняется неравенство

График выпуклой функции расположен под касательной в окрестности точки касания рис. 5б.

y y

y=f(x)

α α

0 x 0 x

а б

Рис. 5

Теорема.Если вторая производная дважды дифференцируемой функции положительна ( отрицательна ) внутри некоторого промежутка Х , то функция вогнута (выпукла ) на этом промежутке.

Таким образом, получаем, если f^//(x)>0 , то функция вогнута, а если f^//(x)<0, то функция выпукла.

Определение.Точкой перегибаграфика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута.

Теорема.Если вторая производнаяf ^//(x) дважды дифференцируемой функции при переходе через некоторую точку х₀ меняет свой знак, то х₀ есть точка перегиба ее графика.

В окрестности точки х₁ функция выпукла и график ее лежит ниже касательной проведенной в этой точке. В окрестности точки х₂, на которой функция вогнута, картина обратная- функция расположена выше касательной. В

0 х₁ х₀х₂ х

Рис.6

точке перегиба х₀ касательная разделяет график- он лежит по разные стороны касательной. Следует отметить, что если критическая точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.

Схема исследования функции на выпуклость, вогнутость и точки перегиба:

1⁰. Найти вторую производную функции f^//(x).

2⁰. Найти точки в которых f^//(x)=0 или не существует.

3⁰. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости, вогнутости и наличии точек перегиба.

4⁰. Найти значения функции в точках перегиба.

Пример. Найти интервалы выпуклости, вогнутости и очкиперегиба графика функции у= х^.(х-1)³.

Решение :

1⁰. Производная. у^/=1^.(х-1)³+3х^.(х-1)²=(х-1)^2.(х-1+3х)=(х-1)^2.(4х- 1);

у^//= 2(х-1)(4х-1)+ (х-1)^2.4=(х-1)^.(8х-2+4х-4)=(х-1)^.(12х-6).

2⁰. у^//=0, (х-1)^.(12х-6)=0

х-1=0 или 12х-6=0

3⁰. у^//>0 на интервалах

, следовательно, на этих интервалах

х=1 х=

у^//+ - +

у 1

функция вогнута; у^//<0 на интервале ( , следовательно на этом интервале функция выпукла, а точки х=1 и х= есть точки перегиба.

4⁰. значения функции в точках перегиба f( )=- , f(1)=0.

2.35. Асимптоты графика функции.

До сих пор изучались характерные точки функции. Теперь рассмотрим характерные линии. Важнейшими линиями являются асимптоты.

Определение. Асимптотой графика функции у=f(x) называется прямая, обладающая тем свойством, что расстояние между точкой Р этого графика и данной прямой стремится к нулю при неограниченном удалении точки Р от начала координат.

у у у

0 х 0 х

0 а

а) б) в)

рис. 7

На рис. 7 а изображена вертикальная асимптота, на рис. 7б –горизонтальная асимптота, а на рис. 7в –наклонная.

Очевидно,, этими тремя случаями исчерпываются все возможные расположения асимптот.

1.Пусть функция y= f(x) определена в некоторой окрестности точки х₀ и предел этой функции при х х₀ равен ∞, т.е. . . Тогда прямая х=х₀ является вертикальной асимптотой графика функции у= f(x).

Очевидно, что прямая х=х₀ не может быть вертикальной асимптотой графика функции , если функция непрерывна в точке х₀, так как в этом случае . Следовательно, вертикальные асимптоты х=х₀ надо искать в точках разрыва функции.

2.Пусть функция определена при достаточно больших х и существует конечный предел функции . Тогда прямая у=b есть горизонтальная асимптота графика функции у= f(x).

В том случае, если , функция может иметь наклонную асимптоту.

3. Пусть функция определена при достаточно больших х и существуют конечные пределы , тогда прямая y=kx+b является наклонной асимптотой графика функции у= f(x).

Пример . Найти асимптоты графика функции

Решении:

Очевидно, что график функции не имеет ни вертикальных асимптот (нет точек разрыва), ни горизонтальных (

Найдем наклонную асимптоту.

Таким образом получаем, наклонная асимптота графика функции имеет вид y= x.

Ответ: у=х.

2.36 Общая схема исследования функций и построения их графиков.

Схема исследования функций:

1⁰.Найти область определения функции.

2⁰. Исследовать функцию на четность – нечетность.

3⁰.Найти вертикальные асимптоты.

4⁰. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.

5⁰. Найти экстремумы и интервалы монотонности функции.

6⁰. найти интервалы выпуклости и точки перегиба.

7⁰. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки уточняющие график.

Пример. Исследовать функцию и построить ее график.

Решение :

1⁰. Область определения : 1-х²≠0

х²≠1

х≠±1 D(x)=(-∞,-1)

2⁰. Функция четная, так как f(-x)= график симметричен относительно оси ординат.

3⁰. Вертикальные асимптоты могут пересекать ось абсцисс в точках х=±1. Так как

, то прямые х=1 и х=-1 есть вертикальные асимптоты.

4⁰. Поведение функции в бесконечности.

Вычислим , т.е. прямая у=-1 есть горизонтальная асимптота.

5⁰. Экстремумы и интервалы монотонности.

у^/=0 , когда числитель равен нулю, т.е. при х=0

у^/ не существует в точках , в которых знаменатель обращается в нуль, т.е. при х=±1.

Однако критической точкой является только точка х=0 (так как значения х=±1 не входят в область определения функции). Найдем знаки производной: у^/ - +

у - 1 0 1 х

х=0-точка минимума, f min=f(0)=1- минимум функции.

На интервалах (-∞,-1) и (-1, 0) функция убывает, на интервалах (0, 1) и (1, +∞) функция возрастает.

6⁰. Интервалы выпуклости и точки перегиба.

Очевидно, что у^//>0 на интервале (-1, 1) и функция вогнута на этом интервале; у^//<0 на интервалах (-∞,-1), (1, +∞) и на этих интервалах функция выпукла. Точек перегиба нет, так как 1+3х²=0

3х²=-1-не имеет смысла.

7⁰. Точки пересечения с осями. f(0)=1, т.е. точка пересечения с осью ординат (0, 1). Уравнение f(x)=0 решений не имеет, следовательно, график функции не пересекает ось абсцисс. График функции изображен на рис. 8.