 |
Главная |
Нахождение производных функций, содержащих степени
|
из
5.00
|
Н.П. Зубарева
Математика
Методическое пособие по изучению темы
"Производная функции"
Калининград, 2015
Составитель: Н.П. Зубарева, канд. пед. наук, доцент.
Рецензент: Ю.Н. Антипов, доктор физмат. наук, профессор.
Методическое пособие предназначено студентам для изучения принципов дифференцирования функций. Подробно пояснено решение отдельных заданий. Для самостоятельного решения предложен ряд заданий, ответы на которые есть на с.20.
В пособии имеется справочный материал.
Печатается по решению
, протокол № от 20 г.
Содержание
1.Формулы дифференцирования. 4
2. Нахождение производных функций, содержащих степени. 6
3. Производная функций, содержащих логарифмы 11
4. Производная, содержащая тригонометрические функции 11.
5. Производная сложной функции 14
6. Производные высших порядков 16
7. Производная функции, заданной неявно. 17
8. Производная степенно-показательной функции
9. Производная функции, заданной параметрически
Ответы.. 20

Формулы дифференцирования
Производная постоянной величины равна нулю: C ' = 0.
Производная аргумента равна единице: x' = 1.
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же алгебраической сумме производных этих функций:

Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй сомножитель плюс произведение первого сомножителя на производную второго сомножителя:
 .
.
Постоянный множитель можно вынести за знак производной:
 , С – постоянная.
, С – постоянная.
Производная частного двух функций может быть найдена по формуле:
. 
Таблица производных
| № п/п | Элементарные функции | № п/п | Сложные функции | ||
| функция у | производная y' | функция у | производная y' | ||
| с | y=f(u); u=φ(x) | 
| |||
| х | |||||
| xn | nxn–1 | un | nun–1 | ||

| 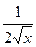
| 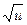
| 
| ||
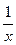
| 
| 
| 
| ||
| ex | ex | eu | eu ∙ u' | ||
| ax | ax lna | аu | а u lna∙ u' | ||
| lnx | 1/x | lnu | 
| ||
| logax | 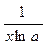
| logau | 
| ||
| sinx | cosx | sinu | cos u ∙ u' | ||
| cosx | –sinx | cosu | –sinx u ∙ u' | ||
| tgx | 
| tgu | 
| ||
| ctgx | 
| ctgu | 
| ||
| arcsinx | 
| arcsinu | 
| ||
| arccosx | 
| arccosu | 
| ||
| arctgx | 
| arctgu | 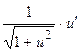
| ||
| arcctgx | 
| arcctgu | 
|
Задание 1.Найти производную функции  .
.
Решение: 
Функция  равна произведению постоянной величины 5 и переменной х2. По формуле
равна произведению постоянной величины 5 и переменной х2. По формуле  выносим постоянную величину перед производной, затем по формуле
выносим постоянную величину перед производной, затем по формуле 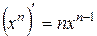 находим производную х2.
находим производную х2.
Задание 2. Найти производную функции  .
.
Решение:

Использовали формулы  ,
,  ,
, 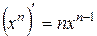
Найти самостоятельно производную функции:
1а) 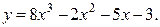
1б) 
Нахождение производных функций, содержащих степени.
Для вычисления производных полезно сначала преобразовать выражение.
Напомним некоторые формулы действий со степенями из школьного курса.
А. 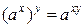 .
.
При возведении степени в степень показатели степеней перемножаются.
Б.  .
.
В.  .
.
Если основания степеней одинаковы, то при умножении показатели степеней складываются, а при делении – показатели степеней вычитаются.
Г. 
Д. 
Е. 
Например:
 .
.

 .
.
 .
.
 .
.
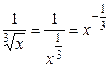 .
.
Задание 3.Найти производную функции  .
.
Решение: Сначала преобразуем по формуле 
 .
.
Производную этой функции найдем по формуле 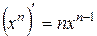
 .
.
Задание 4.Найти производную функции  .
.
Решение: Сначала преобразуем это выражение по формулам  ,
, 
 .
.
Производную этой функции найдем по формулам  ,
, 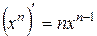
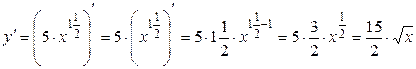 .
.
Производную этого выражения можно найти по формуле  , а потом преобразовать:
, а потом преобразовать:

Задание 5.Найти производную функции  .
.
Решение:

Сначала преобразовали выражение по формулам  ,
,  Производную вычисляли по формулам
Производную вычисляли по формулам  ,
,  ,
, 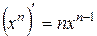 , затем преобразовали полученное выражение по формулам
, затем преобразовали полученное выражение по формулам  ,
, 
Найти самостоятельно производную функции:
2а) 
2б) 
Задание 6.Найти производную функции  .
.
Решение:

Применили формулу  . Далее производные находим по формулам
. Далее производные находим по формулам  ,
, 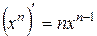 ,
,  ,
,  затем упрощаем полученное выражение, перемножая выражение в скобках.
затем упрощаем полученное выражение, перемножая выражение в скобках.
Найти самостоятельно производную функции:
3а) 
3б) 
Задание 7. Найти производную функции  .
.
Решение:
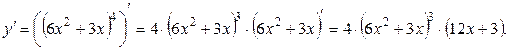
Использовали формулу  , затем формулы
, затем формулы  ,
,  ,
, 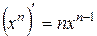 .
.
Найти самостоятельно производную функции:
4а) 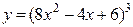 .
.
4а)  .
.
Задание 8. Найти производную функции  .
.
Подставим это выражение в виде степени:
 .
.
Производную найдем сначала по формуле  .
.
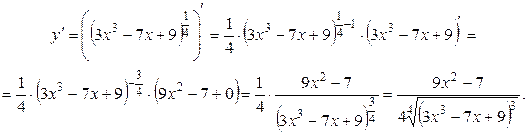
Затем производную находим по формулам  ,
,  ,
, 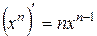 .
.
Найти самостоятельно производную функции:
5а)  .
.
5б)  .
.
Задание 9.Найти производную функции  .
.
Решение: 
Сначала формула  , затем формулы
, затем формулы  ,
,  ,
, 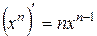 .
.
Найти самостоятельно производную функции:
6а)  .
.
6б)  .
.
Задание 10.Найти производную функции  .
.
Решение: 

Сначала формула 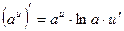 , затем решаем по формулам
, затем решаем по формулам  ,
,  ,
,  ,
, 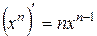 .
.
.
Найти самостоятельно производную функции:
7а)  .
.
7б)  .
.
|
из
5.00
|
Обсуждение в статье: Нахождение производных функций, содержащих степени |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

