 |
Главная |
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №6
|
из
5.00
|
Для заданной рамы (рисунок 26,a) построить эпюру изгибающих моментов при следующих исходных данных: P1=2P, P2=P, M2=Pa.

Рисунок 26 - Расчетная схема рамы и эпюра изгибающих моментов
Определяем опорные реакции рамы. На расчетной схеме (рисунок26, a) показываем векторы опорных реакций RA и HA шарнирно-неподвижной опоры ивектор RB на шарнирно-подвижной опоре B. Величины реакций определяются из уравнений равновесия рамы:
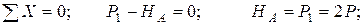



Реакция RА отрицательна, а это значит, что ее направление было выбрано неправильно и его надо изменить на противоположное. В дальнейших расчетах знак минус не учитывается.
Для проверки правильности вычисления опорных реакций подсчитывается сумма проекций сил, приложенных к раме, на вертикальную ось Y:
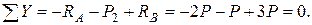
Равенство этой суммы нулю говорит о том, что реакции определены правильно.
Разбиваем раму на участки, границы которых на рисунок26,а обозначены латинскими буквами. В граничных сечениях каждого участка находим величины изгибающих моментов и откладываем полученные значения со стороны сжатого волокна (для удобства построений введем обозначение m=Pa).
С целью вычисления изгибающего момента рассекаем мысленно раму в исследуемом сечении на две части и отбрасываем одну из них, а затем подсчитываем алгебраическую сумму моментов всех сил, приложенных к оставшейся части, относительно рассматриваемого сечения. Эта сумма равна величине изгибающего момента в данном сечении рамы.
Рассмотрим последовательно стержни рамы, начиная со стержня AC, который имеет лишь один участок. Мысленно рассекая стержень в начале участка (левее точки A) и отбрасывая левую часть рамы, вычисляем изгибающий момент в начале участка:
 (сжатые волокна при этом будут находиться снизу).
(сжатые волокна при этом будут находиться снизу).
В конце участка (точка C) величина изгибающего момента равна алгебраической сумме моментов от действия пары сил m2 и реакции RA. Пара сил изгибает стержень AC таким образом, что его сжатые волокна располагаются снизу. Будем считатьусловноизгибающий момент в сечении С, возникающий от действия пары сил, положительным. Тогда изгибающий момент в том же сечении от действия реакции RA следует считать положительным, так как эта сила так же, как и пара сил m2, вызывает сжатие нижних волокон стержня.
Изгибающий момент в сечении С
 .
.
Положительное значение изгибающего момента означает, что сжатые волокна стержня в сечении С по-прежнему остаются снизу. Откладывая в масштабе полученные значения изгибающих моментов перпендикулярно оси стержня AC вниз (со стороны сжатых волокон), строим на этом участке эпюру M, которая будет ограничена прямой линией, так как к раме не приложены распределенные нагрузки.
Переходим к следующему стержню - CE, который разбиваем на два участка - CD и DE.
Участок CD. Изгибающий момент в сечении C, которое принадлежит одновременно стержням AC и CE известен: MC =3Pa.
Сжатые волокна стержня CE в сечении C находится слеваот его оси, следовательно, момент MC = 3Pa надо отложить влево. Изгибающий момент в сечении D

Положительное значение изгибающего момента  означает, что сжатые волокна стержня, как и в сечении C, расположены слева.
означает, что сжатые волокна стержня, как и в сечении C, расположены слева.
Участок DE. Изгибающий момент в сечении D, которое принадлежит теперь рассматриваемому участку DE, MD = 5Pa. Находим изгибающий момент в сечении E:
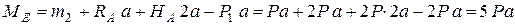 .
.
Перед моментом от силы P1 поставлен знак минус, так как сила P1 сжимает волокна, располагающиеся справа от оси стержня. Положительное значение момента ME = 5Pa означает, что сжатые волокна в сечении располагается слева.
Откладывая ординаты эпюры перпендикулярно оси стержня, как это делалось ранее, строим эпюру на участке DE.
Построение эпюры изгибающих моментов для стержня BE удобно производить, перемещаясь от сечения B справа налево.
Стержень BE.Разбиваем его на два участка: BF и FE. Изгибающий момент в сечении B равен нулю. В сечении F участка BF стержня изгибающий момент равен моменту от действия силы RB = 3P, его величина
 (сжатые волокна находится сверху).
(сжатые волокна находится сверху).
Участок FE. Изгибающий момент в сечении F, принадлежащем этому участку, известен: M=3Pa. В конце участка (сечение E) изгибающий момент  .
.
Первое слагаемое, представляющее момент от действия силы  , вызывающей сжатие верхних волокон стержня, принято положительным. Перед вторым слагаемым поставлен знак минус, так как сжатые волокна от действия силы
, вызывающей сжатие верхних волокон стержня, принято положительным. Перед вторым слагаемым поставлен знак минус, так как сжатые волокна от действия силы  расположены снизу. Положительное значение изгибающего момента в сечении E означает, что сжатые волокна стержня в этом сечении находятся сверху от его оси. Вычисленные ординаты откладываются на эпюре вверх от оси стержня - со стороны сжатых волокон (рисунок26, б).
расположены снизу. Положительное значение изгибающего момента в сечении E означает, что сжатые волокна стержня в этом сечении находятся сверху от его оси. Вычисленные ординаты откладываются на эпюре вверх от оси стержня - со стороны сжатых волокон (рисунок26, б).
Следует обратить внимание на то, что при переходе через узел изгибающий момент по модулю не изменяется и эпюра располагается по одну сторону от контура рамы (внутри или снаружи). Это условие соблюдается, если в узле рамы не приложен сосредоточенный момент (пара сил).
Рассмотрим еще один пример построения эпюры M для рамы.
Требуется построить эпюру изгибающих моментов для рамы, показанной на рисунок27, a.
Исходные данные для расчета: P1 = 2P; P2 = 3P; m1 = 2Pa.
Для рамы, жестко защемленной одним концом, построение эпюры изгибающих моментов рекомендуется начинать с незакрепленного сечения (сечение A на рисунок27, а), не определяя опорных реакций.
Стержень AB (рисунок27,а) имеет один участок, в начале и конце которого вычисляются изгибающие моменты:
MA = 0, MB =  = 2Pa .
= 2Pa .
Откладываем найденные значения слева от оси стержня со стороны его сжатых волокон (рисунок27, б) и соединяем полученные точки прямой линией (равномерно распределенной нагрузки нет!).

Рисунок 27 - Расчетная схема рамы и эпюра изгибающих моментов
Стержень BD имеет два участка - BC и СD. Вычисляются изгибающие моменты в сечениях B, C, D.
В сечении В изгибающий момент MB = 2Pa, так как при переходе через узел величина изгибающего момента не изменяется, сжатые волокна стержня располагаются снизу.
В сечениях С и D изгибающие моменты 
В последнем выражении момент, зависящий от силы P1, условно принят положительным. При этом сжатые волокна стержня BD располагается снизу от его оси. Момент от силы P2 в этом случае отрицателен, так как от действия силы P2 волокна, расположенные снизу, растягиваются. Отрицательное значение изгибающего момента в сечении D, означает, что сжатое волокно теперь располагается теперь не снизу, а сверху от оси стержня. Очевидно, что эпюра М на участке BD ограничена прямыми линиями.
Стержень DE имеет только один участок, в начале которого (сечение D) приложена пара сил с моментом 2Pa. Изгибающий момент в сечении D стержня DE

Найденное значение откладываем справа от оси стержня DE, так как от действия силы P1 сжатые волокна расположены справа, и перед первым слагаемым в выражении для вычисления изгибающего момента поставлен знак плюс, что означает сжатие волокон справа от действия всех внешних сил, приложенных к раме.
Изгибающий момент в сечении E

Здесь знак (плюс или минус) перед каждым слагаемым выбран в соответствии с введенным ранее правилом.
По найденным значениям изгибающих моментов для стержня DE построена эпюра М, ограниченная прямой линией.
Эпюра изгибающих моментов для всей рамы показана на рисунок27,б. Здесь, как и раньше, использовано обозначение m=Pa.
ЗАДАЧА № 7
Для заданной статически неопределимой балки требуется:
1) раскрыть статическую неопределимость;
2) построить эпюру изгибающих моментов;
3) подобрать двутавровое сечение по условию прочности балки;
4) определить угол поворота сечения L и прогиб в сечении К.
Для всех вариантов принять: допускаемое напряжение [s] = 160 МПа, модуль упругости  .
.
Числовые данные берутся из таблице 7, расчетные схемы - по рисунку 28.
Таблица 7 - Числовые данные к задаче № 7
| Номер | Номер расч. | Нагрузка | ||||
| строки | схемы по рисунок28 | q, кН/м | P, кН | P1, кН | m, кН×м | Размер a, м |
| 1,0 | ||||||
| 1,5 | ||||||
| 1,0 | ||||||
| 0,8 | ||||||
| 1,2 | ||||||
| 1,0 | ||||||
| 1,2 | ||||||
| 0,8 | ||||||
| 0,6 | ||||||
| 1,0 |
|
из
5.00
|
Обсуждение в статье: ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №6 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

