 |
Главная |
Основные теоретические сведения и расчетные формулы
|
из
5.00
|
При сжатии гибкого стержня осевой силой возможна потеря его устойчивости, при которой ось стержня искривляется и начальная прямолинейная форма равновесия нарушается. Минимальная сжимающая сила, превышение которой вызывает потерю устойчивости, называется критической силой.
При расчетах сжатых стержней на устойчивость встречаются следующие основные задачи:
1. Вычисление величины критической силы;
2. Определение допускаемого значения сжимающей силы;
3. Подбор сечения стержня по условию его устойчивости;
4. Определение запаса устойчивости стержня.
Величина критической силы вычисляется по формуле Эйлера или Ясинского в зависимости от гибкости рассматриваемого стержня.
Под гибкостью стержня понимается безразмерная величина, вычисляемая по формуле
 (9.1)
(9.1)
где l- длина стержня;
imin - минимальный радиус инерции поперечного сечения;
m - коэффициент, зависящий от способа закрепления концов стержня.
Его значения для наиболее распространенных способов закрепления приведены в таблице 10
Формула Эйлера применима при условии, что критическое напряжение, равное 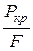 , не превышает предела пропорциональности материала стержня. Обычно это условие выражается формулой
, не превышает предела пропорциональности материала стержня. Обычно это условие выражается формулой
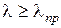 , (9.2)
, (9.2)
где  - предельная гибкость стержня.
- предельная гибкость стержня.
Для каждого материала  определяется по выражению
определяется по выражению
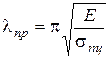 , (9.3)
, (9.3)
где Е - модуль упругости материала;
sпц - предел пропорциональности материала стержня.
Например,для стали марки Ст.3 при E = 2×105МПа, sпц = 200МПа и предельная гибкость lпр =100.
Если расчетная гибкость стержня больше или равна предельной, то для вычисления критической силы применяется формула Эйлера:
 (9.4)
(9.4)
если гибкость меньше предельной, то для вычисления критической силы используется эмпирическая формула, предложенная Ясинским:
 (9.5)
(9.5)
(для стали Ст3 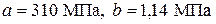 ).
).
Наряду с расчетами по формуле Эйлера или Ясинского при расчетах сжатых стержней на устойчивость широко применяется метод, в котором условие устойчивости сжатого стержня записывается в следующем виде:

 [s]у = j × [s]с, (9.6)
[s]у = j × [s]с, (9.6)
где N- сжимающая сила;
F - площадь поперечного сечения стержня;
[s]у - допускаемое напряжение при расчете стержня на устойчивость;
[s]с - допускаемое напряжение материала стержня при сжатии;
j - коэффициент снижения допускаемого напряжения.
Величина коэффициента j зависит от гибкости стержня l и материала, из которого он изготовлен. Для малоуглеродистой стали (Ст.3) его можно определить по табл.11.
Таблица 10 - Коэффициенты приведения длины m
| Схема закрепления | ||||
Коэффициент

| 0,7 | 0,5 |

|

|
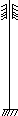
|
в зависимости от способа закрепления концов cтержня
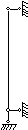
|
Таблица 11 - Величины коэффициентов j для стали Ст. 3 в зависимости от гибкости l
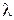
| 
| 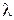
| 
| 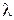
| 
|
| 1,00 0,99 0,96 0,94 0,92 0,89 0,86 | 0,81 0,75 0,69 0,60 0,52 0,45 0,40 | 0,36 0,32 0,29 0,26 0,23 0,21 0,199 |
Условие устойчивости позволяет найти допускаемое значение сжимающей силы:

 j × [s]сж. (9.7)
j × [s]сж. (9.7)
Поскольку условие устойчивости включает в себя два параметра 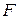 и j, зависящие друг от друга, при подборе сечения стержня следует использовать способ проб, заключающийся в том, что задаются значением одного из параметров, например j, определяют из условия устойчивости площадь сечения, а затем проверяют, удовлетворяется ли условие
и j, зависящие друг от друга, при подборе сечения стержня следует использовать способ проб, заключающийся в том, что задаются значением одного из параметров, например j, определяют из условия устойчивости площадь сечения, а затем проверяют, удовлетворяется ли условие
 = j × [s]сж.
= j × [s]сж.
Если условие удовлетворяется, то расчет на этом заканчивается, если нет, то задаются новым значением  и аналогичный расчет повторяется до тех пор, пока условие устойчивости не будет удовлетворено.
и аналогичный расчет повторяется до тех пор, пока условие устойчивости не будет удовлетворено.
Запас устойчивости 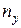 сжатого стержня
сжатого стержня
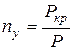 (9.8)
(9.8)
показывает, во сколько раз критическая сила больше заданной или допускаемой.
|
из
5.00
|
Обсуждение в статье: Основные теоретические сведения и расчетные формулы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

