Последовательности. Предел последовательности. Свойства сходящихся последовательностей

Последовательности

Определение. Если каждому натуральному числу ставится в соответствие по определенному закону некоторое вещественное число , то множество занумерованных чисел называют числовой последовательностью или просто последовательностью.

Числа называются элементами или членами последовательности. По своему определению последовательность содержит бесконечное множество элементов. Последовательность с элементами обозначают также { }.

Например, — это последовательность , — это последовательность 0, 2, 0, 2, …

Заметим, что числовая последовательность является частным случаем функции. Можно сказать, что последовательность — это функция , определенная на множестве натуральных чисел и принимающая значения из множества вещественных чисел.

Последовательность может быть задана с помощью формулы , которая называется формулой общего члена последовательности. Например, формула задает последовательность

Суммой двух последовательностей и называется последовательность , все элементы которой равны сумме .

Разностью двух последовательностей и называется последовательность , все элементы которой равны разности .

Произведением двух последовательностей и называется последовательность = , частным — последовательность = , причем при определении частного нужно потребовать, чтобы все элементы последовательности были отличны от нуля.

Ограниченные и неограниченные последовательности

Последовательность называется ограниченной, если найдется положительное число 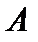такое, что для всех членов последовательности справедливо неравенство .

Последовательность называется неограниченной, если для любого положительного числа 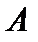найдется хотя бы один элемент последовательности, удовлетворяющий неравенству .

Предел последовательности

Определение 1. Число называется пределом последовательности , если для любого положительного числа найдется такой номер , зависящий от , что при все элементы этой последовательности удовлетворяют неравенству

. (1)

Последовательность , имеющая предел, называется сходящейся последовательностью.

Предел последовательности обозначается символом . Фраза «предел последовательности равен » записывается следующим образом.

, или при .

Неравенство (1) означает, что, начиная с номера , все элементы последовательности находятся внутри интервала , который называют -окрестностью числа .Определение 2. Последовательность называется сходящейся, если существует такое число , что в любой -окрестности числа находятся все элементы данной последовательности, начиная с некоторого номера.

Последнее утверждение означает, что, если число — предел последовательности, то за пределами любой его -окрестности находится лишь конечное число элементов данной последовательности.

Последовательность, которая не является сходящейся, называется расходящейся. Из определения 2 следует, что последовательность расходится, если для любого числа найдется его -окрестность, за пределами которой лежит бесконечное число элементов последовательности.

Пример 1. Доказать, что предел последовательности равен 1.

Пусть — произвольное положительное число. Заметим, что при всех . Тогда за номер можно принять натуральное число , где — целая часть числа . Поскольку для произвольного числа мы смогли определить номер такой, что при всех справедливо неравенство , то .

Пример. Доказать, что последовательность расходится.

Действительно, данная последовательность — это последовательность 1, 0, -1, 0, 1, 0, -1, … Пусть . Если, число принадлежит интервалу , то в -окрестность этого числа попадут лишь члены последовательности, равные нулю, а бесконечное число членов, равных 1 или –1, окажутся за пределами -окрестности. Если число принадлежит интервалу (0,9;1,1) или (-1,1;-0,9), то за пределами -окрестности заведомо окажутся все нулевые члены последовательности. При всех остальных значениях числа при достаточно малых значениях в -окрестность не попадет ни одного члена последовательности. Итак какое бы число мы не взяли, для заданного найдется бесконечное число элементов последовательности, не принадлежащих -окрестности числа . Следовательно, рассматриваемая последовательность расходится.

Предел функции.

Предельное значение функции пр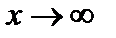и , и

Будем считать, что область задания функции имеет хотя бы один элемент, лежащий вне отрезка , для любого положительного числа .

Определение (по Коши). Число называется пределом функции при 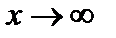, если для любого положительного числа найдется такое положительное число , что для всех значений аргумента функции , удовлетворяющих условию , справедливо неравенство .

В доказательствах нередко удобнее пользоваться другим эквивалентным определением предельного значения.

Определение (по Гейне). Число называется пределом функции при 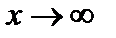, если для любой бесконечно большой последовательности значений аргумента функции соответствующая последовательность значений функции сходится к .

Пример. Найдем предел функции при 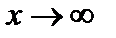. Пусть — произвольная бесконечно большая последовательность. Тогда соответствующая последовательность значений функции является бесконечно малой. Следовательно .

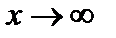Пример. Покажем, что функция не имеет предела при . Действительно, для бесконечно большой последовательности соответствующая последовательность значений функции сходится к 1. Однако для другой бесконечно большой последовательности соответствующая последовательность значений функции сходится к 0. Следовательно, предел функции при 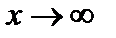не существует.

Сформулируем определение предела функции при стремлении аргумента 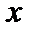к бесконечности определенного знака, то есть при и . Предельные значения функции в этих случаях могут оказаться различными.

Определение (по Гейне). Число называется пределом функции при ( ), если для любой бесконечно большой последовательности значений аргумента функции, элементы которой, начиная с некоторого номера, положительны (отрицательны), соответствующая последовательность значений функции сходится к .

Пример. Найти предельные значения функции при и .

На рис. 1 приведен график заданной функции. Мы видим, что при график функции приближается к прямой , а при — к прямой . Покажем, что , а .

Пусть — произвольная бесконечно большая последовательность, все элементы которой, начиная с некоторого номера, положительны. Тогда

Рис. 1 .

Если все члены бесконечно большой последовательности , начиная с некоторого номера, отрицательны, то

.

Следовательно, , а .

Односторонние пределы

Определение. Число называется правым (левым) пределом функции в точке , если для любой сходящейся к последовательности значений аргумента функции, все элементы которой больше (меньше) , соответствующая последовательность значений функции сходится к .

Такие пределы называются односторонними пределами.

Правый предел обозначают символом , а левый — . Правый и левый предел функции в точке могут принимать как равные, так и отличные друг о друга значения.

Пример. Найдем правый и левый пределы функции при . Возьмем произвольную сходящуюся к последовательность , все элементы которой больше нуля. Тогда и . Пусть все члены сходящейся к последовательности меньше нуля. В этом случае и .

Теорема. Если в точке правые и левые пределы функции равны, то в этой точке существует предельное значение функции, равное указанным односторонним пределом.