Точки перегиба. Необходимое и достаточное условия существования точки перегиба, направление выпуклости

Точки перегиба графика функции

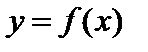Определение. Точка графика функции называется точкой перегиба этого графика, если существует такая окрестность точки оси абсцисс, в пределах которой график функции справа и слева от точки имеет разные направления выпуклости.

Если функция дифференцируема в точке и ее окрестности, то геометрически это означает, что график функции переходит в окрестности точки с одной стороны касательной на другую (рис. 3).

Если функция непрерывна в точке , дифференцируема в окрестности точки , за исключением самой точки , и 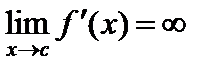, то график функции в окрестности точки находится по разные стороны от вертикальной касательной (рис. 4).

Рис. 3 Рис. 4

Теорема 3 (необходимое условие существования точки перегиба). Пусть функция имеет в точке непрерывную вторую производную. Тогда, если точка является точкой перегиба графика функции, то .

Заметим, что условие является необходимым, но недостаточным условием перегиба графика функции в точке . Рассмотрим, например функцию 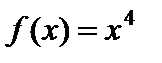. Вторая производная этой функции , обращается в нуль точке . Однако на всей числовой оси , следовательно, всюду на этой оси график функции имеет выпуклость, направленную вниз, и точка 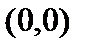не является точкой перегиба.

Теорема 4 (достаточное условие наличия точки перегиба). Если функция дифференцируема в точке , дважды дифференцируема в некоторой окрестности точки , за исключением, быть может, самой точки и вторая производная меняет знак при переходе аргумента через точку , то точка является точкой перегиба графика функции.

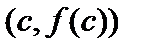Заметим, что если функция непрерывна в точке , дважды дифференцируема в некоторой окрестности точки , за исключением самой точки , и имеет в точке касательную (хотя бы параллельную оси ), то утверждение теоремы 4 также справедливо.

Пример 1. Найти точки перегиба графика функции .

Найдем производные заданной функции:

,

.

Вторая производная

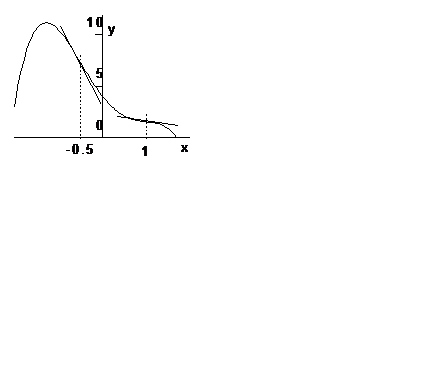обращается в нуль в точках , и меняет знак при переходе через эти точки. Следовательно, точки и являются точками перегиба графика функции. Заметим также, что на интервалах 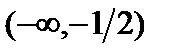и , следовательно, график функции имеет выпуклость, направленную вверх. На интервале , и график функции имеет выпуклость, направленную вниз.

Пример 2. Найти точки перегиба графика функции .

Эта функция непрерывна на всей числовой оси и имеет конечную вторую производную всюду на числовой прямой, за исключением точки . Причем при , а при 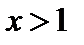. В точке первая производная функции не определена. Поскольку , то график функции имеет в точке (1,2) вертикальную касательную. Так как вторая производная меняет знак при переходе через точку , то точка (1,2) является точкой перегиба.

Направление выпуклости графика функции

Пусть функция дифференцируема в любой точке интервала , то есть имеет в любой точке этого интервала конечную производную. Тогда существует касательная к графику функции , проходящая через любую точку этого графика , причем эта касательная не параллельна оси .

Определение. Говорят, что график функции имеет на интервале выпуклость, направленную вниз (вверх), если график этой функции лежит не ниже ( не выше) любой своей касательной.

На рис. 1 изображен график функции, выпуклой вниз, а на рис. 2 — выпуклой вверх.

Рис. 1 Рис. 2

Теорема 1. Если функция имеет на интервале конечную вторую производную и если эта производная неотрицательна (неположительна) всюду на этом интервале, то график функции имеет на интервале выпуклость, направленную вниз (вверх).

Теорема 2. Пусть вторая производная функции непрерывна и положительна (отрицательна) в точке , тогда существует такая окрестность точки , в пределах которой график функции имеет выпуклость, направленную вниз (вверх).