 |
Главная |
Асимптоты графика функции
|
из
5.00
|
Асимптоты графика функции
Определение. Прямая  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений  или
или  равно
равно  или
или  .
.
Заметим, что если прямая  , является вертикальной асимптотой, то точка
, является вертикальной асимптотой, то точка  — это точка разрыва второго рода, в которой функция
— это точка разрыва второго рода, в которой функция  не определена. Поэтому для того, чтобы найти вертикальные асимптоты нужно исследовать точки, в которых функция не определена.
не определена. Поэтому для того, чтобы найти вертикальные асимптоты нужно исследовать точки, в которых функция не определена.
Определение. Прямая  называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  при
при 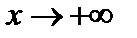 (
( 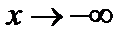 ), если
), если 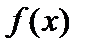 представима в виде
представима в виде  , где
, где  — бесконечно малая функция при
— бесконечно малая функция при 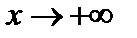 (
( 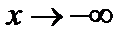 ).
).
Теорема. Для того, чтобы график функции  имел наклонную асимптоту, необходимо и достаточно, чтобы существовали два конечных предельных значения
имел наклонную асимптоту, необходимо и достаточно, чтобы существовали два конечных предельных значения
 , (1)
, (1)
 . (2)
. (2)
Пример. Найти асимптоты графика функции  .
.
Данная функция не определена в точке  . Найдем предельное значение функции при
. Найдем предельное значение функции при 
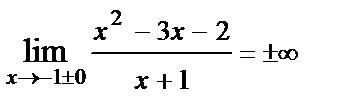 .
.
Следовательно, график этой функции имеет вертикальную асимптоту  .
.
Чтобы выяснить, есть ли у графика функции наклонные асимптоты, найдем предельные значения (1), (2):
 ,
,
 .
.
Итак, прямая 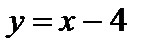 является наклонной асимптотой графика при
является наклонной асимптотой графика при 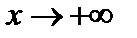 и
и 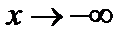 .
.
19.ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Понятие первообразной функции
Определение. Функция  называется первообразной функцией для функции
называется первообразной функцией для функции  на интервале
на интервале  , если в любой точке
, если в любой точке 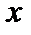 этого интервала функция
этого интервала функция  дифференцируема, и ее производная
дифференцируема, и ее производная  равна
равна  .
.
Свойства первообразных
1) Если функция  является первообразной функцией для функции
является первообразной функцией для функции  на интервале
на интервале  , то и функция
, то и функция 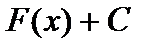 , где
, где  — произвольная постоянная, также является первообразной функцией для функции
— произвольная постоянная, также является первообразной функцией для функции  на интервале
на интервале  .
.
Действительно,
 .
.
2) Если  и
и  — первообразные функции для функции
— первообразные функции для функции  на интервале
на интервале  , то повсюду на этом интервале
, то повсюду на этом интервале  , где
, где  — некоторая постоянная.
— некоторая постоянная.
Положим  . Так как каждая из функций
. Так как каждая из функций  и
и  дифференцируема на интервале
дифференцируема на интервале  , то и
, то и 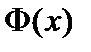 дифференцируема на этом интервале. Причем всюду на интервале
дифференцируема на этом интервале. Причем всюду на интервале  справедливо равенство
справедливо равенство
 .
.
Так как производная  равна нулю в любой точке интервала
равна нулю в любой точке интервала  , то функция
, то функция 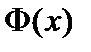 является постоянной на этом интервале.
является постоянной на этом интервале.
3) Если функция  является первообразной функцией для функции
является первообразной функцией для функции  на интервале
на интервале  , то любая первообразная функция
, то любая первообразная функция 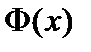 для функции
для функции  на интервале
на интервале  имеет вид
имеет вид  , где
, где  — некоторая постоянная.
— некоторая постоянная.
Это утверждения является следствием свойства 2.
Неопределенный интеграл
Определение. Совокупность всех первообразных функции  на интервале
на интервале  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом 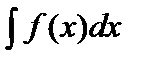 . В этом обозначении знак
. В этом обозначении знак  называется знаком интеграла,
называется знаком интеграла,  — подынтегральным выражением,
— подынтегральным выражением,  — подынтегральной функцией,
— подынтегральной функцией, 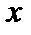 . — переменной интегрирования.
. — переменной интегрирования.
Если функция  является первообразной функцией для функции
является первообразной функцией для функции  на интервале
на интервале  , то в силу приведенного выше следствия
, то в силу приведенного выше следствия
 ,
,
где  — произвольная постоянная.
— произвольная постоянная.
Заметим также, что, если для функции  на интервале
на интервале  существует первообразная функция, то подынтегральное выражение представляет собой дифференциал любой первообразной. Действительно, если
существует первообразная функция, то подынтегральное выражение представляет собой дифференциал любой первообразной. Действительно, если  является первообразной функцией для функции
является первообразной функцией для функции  на интервале
на интервале  , то
, то  .
.
20.Свойства неопределенного интеграла.
Пусть функция  имеет на некотором интервале первообразную функцию
имеет на некотором интервале первообразную функцию  . Неопределенный интеграла имеет следующие свойства:
. Неопределенный интеграла имеет следующие свойства:
1.  .
.
Действительно, используя определение неопределенного интеграла, имеем
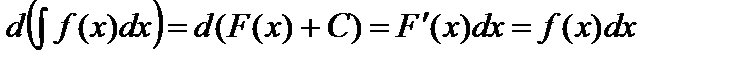 .
.
2.  .
.
Так как  , а первообразной для функции
, а первообразной для функции  является функция
является функция  , то согласно определению неопределенного интеграла получим
, то согласно определению неопределенного интеграла получим
 .
.
3.  .
.
Пусть 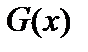 — первообразная для функции
— первообразная для функции  . Тогда свойство 3 можно записать в виде
. Тогда свойство 3 можно записать в виде
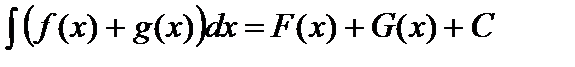 ,
,
Следовательно, свойство 3 означает, что 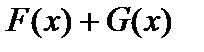 — это первообразная для функции
— это первообразная для функции  . Покажем, что последнее утверждение справедливо. Действительно,
. Покажем, что последнее утверждение справедливо. Действительно,
 .
.
4.  , где
, где  — некоторая постоянная.
— некоторая постоянная.
Перепишем свойство 4 в виде 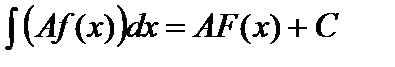 и покажем, что
и покажем, что  является первообразной функцией для функции
является первообразной функцией для функции  . Действительно,
. Действительно,
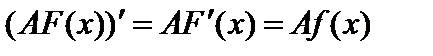 .
.
5.  , где
, где  — первообразная функции
— первообразная функции  .
.
Пусть  . Тогда
. Тогда
 .
.
Следовательно,  является первообразной подынтегральной функции
является первообразной подынтегральной функции  .
.
21.Таблица интегралов.
Поскольку неопределенный интеграл — это совокупность первообразных  для подынтегральной функции, то для нахождения неопределенного интеграла
для подынтегральной функции, то для нахождения неопределенного интеграла  , требуется отыскать функцию
, требуется отыскать функцию  , удовлетворяющую соотношению
, удовлетворяющую соотношению  . Непосредственной проверкой этого соотношения можно убедиться в справедливости следующих формул.
. Непосредственной проверкой этого соотношения можно убедиться в справедливости следующих формул.
1. 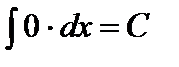 .
.
2.  .
.
3.  (
( 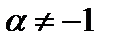 ).
).
4.  (
(  ).
).
5. 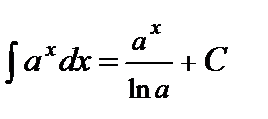 ,
, 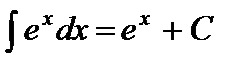 .
.
6.  .
.
7. 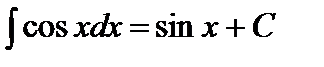 .
.
8.  ,
, 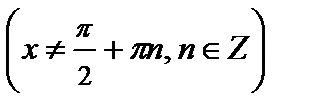 .
.
9.  ,
,  .
.
10. 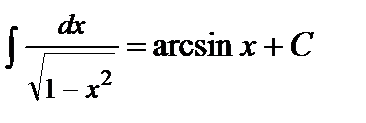 ,
,  .
.
11. 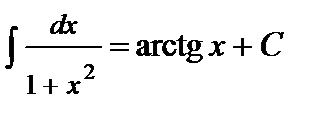 .
.
12.  , (
, ( 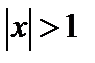 , если в подкоренном выражении выбран знак –).
, если в подкоренном выражении выбран знак –).
13.  ,
, 
15.  (
(  ).
).
16.  , (
, (  ,
, 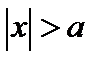 , если выбран знак –).
, если выбран знак –).
17.  , (
, (  ,
,  ).
).
18.  .
.
19.  .
.
20.  .
.
22.Методы интегрирования:замена переменной.
Замена переменной в неопределенном интеграле
Теорема. Пусть функция 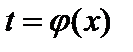 определена и непрерывна на множестве
определена и непрерывна на множестве 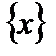 и пусть
и пусть  — множество всех значений этой функции. Пусть далее для функции
— множество всех значений этой функции. Пусть далее для функции  существует на множестве
существует на множестве  первообразная функция
первообразная функция  , то есть
, то есть
 .
.
Тогда всюду на множестве 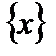 для функции
для функции  существует первообразная функция, равная
существует первообразная функция, равная  , то есть
, то есть
 .
.
Доказательство. Поскольку
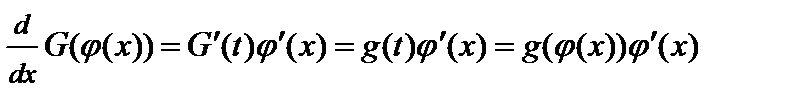 ,
,
то функция  является первообразной для функции
является первообразной для функции  .
.
Замена переменной является одним из основных методов интегрирования. Предположим, что нам удалось выбрать в качестве новой переменной такую дифференцируемую функцию 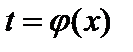 , что подынтегральная функция
, что подынтегральная функция  может быть представлена в виде
может быть представлена в виде  , а интеграл
, а интеграл  легко вычисляется, тогда на основании теоремы о замене переменной в неопределенном интеграле имеем
легко вычисляется, тогда на основании теоремы о замене переменной в неопределенном интеграле имеем
 . (1)
. (1)
Добавим теперь к таблице основных интегралов несколько часто встречающихся интегралов, которые мы найдем с помощью замены переменной.
17.  ,
,  .
.
Сделаем замену переменной  , тогда
, тогда 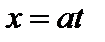 ,
, 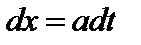 ,
, 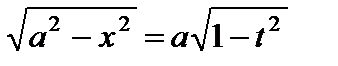 и
и
 .
.
18.  (
(  ).
).
В этом интеграле также сделаем замену переменной  . В результате получим
. В результате получим
 .
.
19.  , (
, (  ,
, 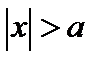 , если выбран знак –).
, если выбран знак –).
Этот интеграл с помощью замены переменной  можно свести к интегралу 12.
можно свести к интегралу 12.

 .
.
Заметим, что поскольку 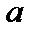 — некоторая положительная постоянная, то
— некоторая положительная постоянная, то 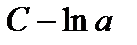 — это произвольная постоянная, поэтому в формуле (19)
— это произвольная постоянная, поэтому в формуле (19) 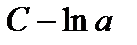 заменили на
заменили на  .
.
20.  , (
, (  ,
,  ).
).
Преобразуем подынтегральную функцию к виду
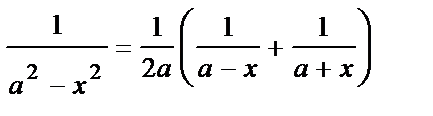
и рассмотрим интегралы  и
и  . В первом интеграле сделаем замену переменной
. В первом интеграле сделаем замену переменной 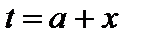 , а во втором
, а во втором  . Тогда
. Тогда  ,
,  . В результате замены получим
. В результате замены получим

 ,
,  .
.
 Далее воспользуемся свойствами 3 и 4 неопределенного интеграла
Далее воспользуемся свойствами 3 и 4 неопределенного интеграла

 .
.

 21.
21.  .
.
 Преобразуем подынтегральную функцию
Преобразуем подынтегральную функцию

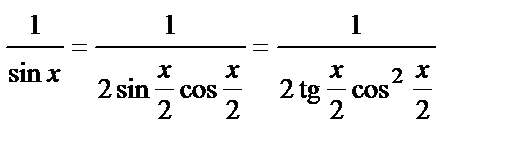
 и сделаем замену переменной
и сделаем замену переменной  . Тогда
. Тогда  и
и

 .
.
 22.
22.  .
.
 Заметим, что
Заметим, что  , и сделаем замену переменной
, и сделаем замену переменной  . В результате получим
. В результате получим

 .
.
 23.
23.  .
.
 Этот интеграл вычисляется с помощью замены переменной
Этот интеграл вычисляется с помощью замены переменной  . При этом
. При этом  и
и

 .
.
 При интегрировании путем замены переменной преобразования (1) нередко записывают в сокращенном виде
При интегрировании путем замены переменной преобразования (1) нередко записывают в сокращенном виде

 . (2)
. (2)

 В этом случае, говорят, что функция
В этом случае, говорят, что функция  подведена под знак дифференциала. При такой форме записи вычисление интеграла 23 приобретает вид
подведена под знак дифференциала. При такой форме записи вычисление интеграла 23 приобретает вид
 .
.
Приведем еще несколько примеров.
Пример 1.  . В этом интеграле фактически была сделана замена
. В этом интеграле фактически была сделана замена 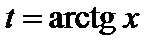 , но часть преобразований
, но часть преобразований

опущена.
Пример 2.  . В данной записи вычисления интеграла мы опять опустили часть преобразований, подведя под знак дифференциала функцию
. В данной записи вычисления интеграла мы опять опустили часть преобразований, подведя под знак дифференциала функцию 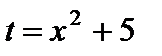 .
.
Пример 3.  . Здесь по знак дифференциала подведена функция
. Здесь по знак дифференциала подведена функция  .
.
23.Интегрирование по частям.
Формула интегрирования по частям
Пусть каждая из функций  и
и  дифференцируема на множестве
дифференцируема на множестве 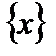 и, кроме того, на этом множестве существует первообразная для функции
и, кроме того, на этом множестве существует первообразная для функции 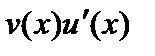 . Тогда на множестве
. Тогда на множестве 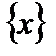 существует первообразная и для функции
существует первообразная и для функции 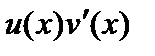 , причем справедлива формула
, причем справедлива формула
 . (1)
. (1)
Доказательство. Воспользуемся формулой производной произведения двух функций
 .
.
Умножим это равенство на  и возьмем интеграл от правой и левой части
и возьмем интеграл от правой и левой части
 .
.
Так как  , а интеграл
, а интеграл  существует , то существует и интеграл
существует , то существует и интеграл  , причем
, причем
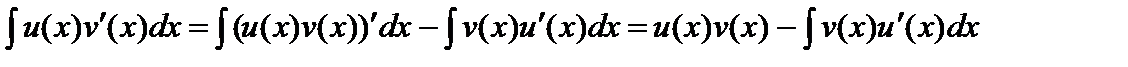 .
.
Учитывая, что  , а
, а  , формулу (1) можно записать в виде
, формулу (1) можно записать в виде
 . (2)
. (2)
Пример 1. Найти интеграл  .
.
Применим формулу интегрирования по частям (4), полагая  ,
,  ,
, 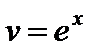 ,
,  . В результате получим
. В результате получим
 .
.
Пример 2. Найти интеграл 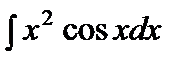 .
.
Полагая в формуле интегрирования по частям (2)  ,
,  ,
, 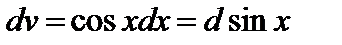 , получим
, получим
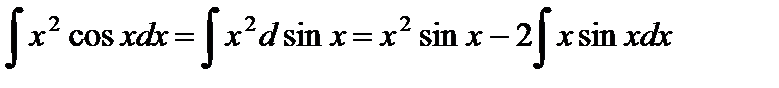 .
.
Для вычисления интеграла  еще раз применим формулу (2) (
еще раз применим формулу (2) (  ,
,  ,
,  ,
,  ). В результате имеем
). В результате имеем

=  .
.
Пример 3. Найти интеграл  .
.
Пусть  ,
, 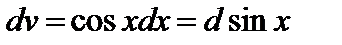 . Тогда по формуле (2)
. Тогда по формуле (2)
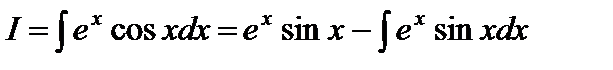 ,
,
При вычислении интеграла 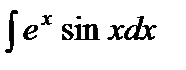 снова используем формулу интегрирования по частям (
снова используем формулу интегрирования по частям (  ,
,  )
)
 .
.
В результате мы получили линейное алгебраическое уравнение относительно 
 .
.
Решая его, находим
 .
.
Пример 4. Найти интеграл  .
.
Пусть 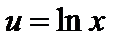 ,
,  . Тогда по формуле интегрирования по частям имеем
. Тогда по формуле интегрирования по частям имеем
 .
.
С помощью интегрирования по частям вычисляются интегралы следующих видов:
1) 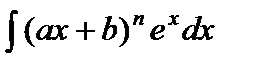 ,
,  ,
, 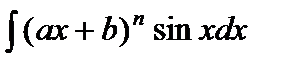 .
.
При вычислении этих интегралов следует положить  . Поскольку
. Поскольку  , то в результате интегрирования по частям получатся интегралы вида
, то в результате интегрирования по частям получатся интегралы вида
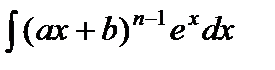 ,
, 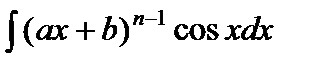 ,
, 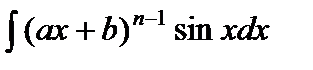 .
.
Применяя формулу интегрирования по частям  раз придем к табличным интегралам
раз придем к табличным интегралам
 ,
,  ,
,  .
.
2)  ,
,  .
.
Применяя дважды формулу интегрирования по частям  , приходим к уравнению первого порядка относительно рассматриваемого интеграла. Решив это уравнение найдем искомый интеграл.
, приходим к уравнению первого порядка относительно рассматриваемого интеграла. Решив это уравнение найдем искомый интеграл.
3) Подынтегральная функция содержит множитель: 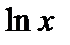 ,
,  ,
,  ,
,  .
.
В этом случае в формуле интегрирования по частям надо положить функцию  , равной одной из указанных функций.
, равной одной из указанных функций.
24.Определенный интеграл, его геометрический смысл.
Определение. Функция  называется интегрируемой по Риману на отрезке
называется интегрируемой по Риману на отрезке  , если существует конечный предел
, если существует конечный предел  интегральных сумм этой функции при
интегральных сумм этой функции при  . Указанный предел
. Указанный предел  интегральных сумм называется определенным интегралом функции
интегральных сумм называется определенным интегралом функции  на отрезке
на отрезке  и обозначается
и обозначается 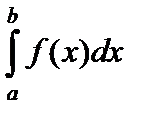 .
.
Итак
 .
.
В записи определенного интеграла  называют нижним пределом интегрирования,
называют нижним пределом интегрирования,  — верхним пределом интегрирования,
— верхним пределом интегрирования,  — подынтегральной функцией, отрезок
— подынтегральной функцией, отрезок  — интервалом интегрирования.
— интервалом интегрирования.
Из определения определенного интеграла следует, что для неотрицательных функций определенный интеграл является пределом при  последовательности площадей рассмотренных выше ступенчатых фигур. Поэтому он равен площади фигуры, ограниченной графиком функции
последовательности площадей рассмотренных выше ступенчатых фигур. Поэтому он равен площади фигуры, ограниченной графиком функции  , отрезком
, отрезком  оси
оси  и прямыми
и прямыми  ,
, 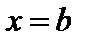 . Позже мы докажем это утверждение более строго.
. Позже мы докажем это утверждение более строго.
Геометрический смысл определенного интеграла
Пусть функция  непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  . Криволинейной трапецией называется фигура
. Криволинейной трапецией называется фигура  , ограниченная прямыми
, ограниченная прямыми  ,
,  , осью
, осью  и графиком функции
и графиком функции  (рис. 3)
(рис. 3)

Рис. 3
Заметим, что нижняя сумма Дарбу 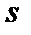 представляет собой площадь ступенчатой фигуры, вписанной в криволинейную трапецию, а верхняя сумма Дарбу
представляет собой площадь ступенчатой фигуры, вписанной в криволинейную трапецию, а верхняя сумма Дарбу  — площадь ступенчатой фигуры, описанной вокруг криволинейной трапеции. Очевидно, что
— площадь ступенчатой фигуры, описанной вокруг криволинейной трапеции. Очевидно, что
 ,
,
где  — площадь криволинейной трапеции. Так как непрерывная на отрезке
— площадь криволинейной трапеции. Так как непрерывная на отрезке  функция интегрируема на этом отрезке, то
функция интегрируема на этом отрезке, то
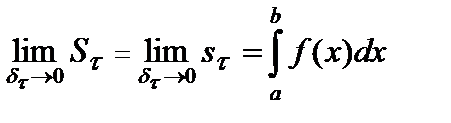 .
.
Следовательно,
 .
.
Итак, определенный интеграл  от непрерывной неотрицательной функции равен площади криволинейной трапеции, ограниченной прямыми
от непрерывной неотрицательной функции равен площади криволинейной трапеции, ограниченной прямыми  ,
,  , осью
, осью  и графиком функции
и графиком функции 
25.Формула Ньютона-Лейбница.
Пусть функция  непрерывна на отрезке
непрерывна на отрезке  , тогда любая ее первообразная может быть представлена в виде
, тогда любая ее первообразная может быть представлена в виде
 . (3)
. (3)
Положим в формуле (3) сначала  , а затем
, а затем  . В результате имеем два равенства
. В результате имеем два равенства
 ,
,  .
.
Вычитая из второго равенства первое и заменяя  на
на  , получим основную формулу интегрального исчисления
, получим основную формулу интегрального исчисления
 . (4)
. (4)
Эту формулу называют также формулой Ньютона-Лейбница.
Разность  обозначают символом
обозначают символом  , формулу (4) записывают в виде
, формулу (4) записывают в виде 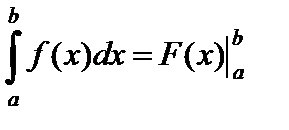 .
.
Из формулы Ньютона-Лейбница следует, что для вычисления определенного интеграла нужно найти какую-либо первообразную подынтегральной функции и из значения этой первообразной для верхнего предела интегрирования вычесть значение для нижнего предела.
Пример.  .
.
|
из
5.00
|
Обсуждение в статье: Асимптоты графика функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

