Свойства определенного интеграла

1. Будем считать, что .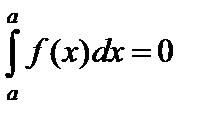

2. ( ).

Интеграл мы определили как предел интегральной суммы , когда мелкость разбиения стремится к нулю. При этом мы разбили отрезок точками такими, что

,

и обозначили через разность .

Если отрезок пробегается в направлении от к , то, следуя формальному определению интегральной суммы, мы должны положить

.

Тогда все станут отрицательными, и все слагаемые в интегральной сумме изменят знак на противоположный.

3. Пусть функции и интегрируемы на отрезке . Тогда функции , также интегрируемы на этом отрезке, причем

. (1)

Докажем интегрируемость функций , и справедливость формулы (1). Действительно,

.

4. Если функция интегрируема на отрезке , то функция , также интегрируема на этом отрезке, причем

.

Действительно,

.

5. Если функция интегрируема на отрезке , то она интегрируема на любом отрезке , содержащемся в .

6. Если функция интегрируема на отрезках и , то она интегрируема на отрезке . Причем

.

Следующие свойства связаны с оценками интегралов.

7. Если интегрируемая на отрезке функция неотрицательна на этом отрезке, то .

Рассмотрим интегральную сумму 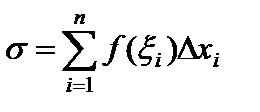. Так как 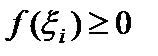, и , то и .

8. Если функция интегрируема на отрезке и всюду на этом отрезке, то .

Заметим, что , и по свойству 7 . Отсюда .

9. Если функции и интегрируемы на отрезке и всюду на этом отрезке, то .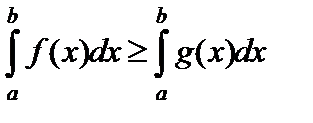

Так как всюду на отрезке и функция интегрируема на этом отрезке, то по свойству 7 имеем . Отсюда следует свойство 10.

10. Если функция интегрируема на отрезках , то функция также интегрируема на этом отрезке, причем

. (2)

Действительно, поскольку для функции справедливо неравенство

,

то согласно свойству 9 имеем

,

откуда следует неравенство (2).

11. Пусть функция интегрируема на отрезке . Тогда, если и — наибольшее и наименьшее значения функции на отрезке , то

. (4)

Поскольку для любого из отрезка справедливы неравенства , то

. (5)

Ранее мы установили, что . Подставляя значение интеграла в (5) получим (4).

12. Теорема о среднем. Пусть функция непрерывна на отрезке . Тогда найдется такая точка , принадлежащая отрезку , что

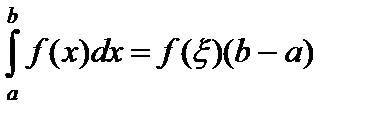. (6)

Заметим, что непрерывная на отрезке функция интегрируема на этом отрезке. Воспользуемся свойством 12. Разделим неравенства (4) на . В результате получим

.

Обозначая через число , получим неравенства .

Если функция непрерывна на отрезке , то она достигает на этом отрезке своих наибольшего и наименьшего значений и принимает все промежуточные значения от до . Следовательно, найдется такая точка , принадлежащая отрезку , что . Тогда имеем . Отсюда следует формула (6).