 |
Главная |
Определение допускаемых напряжений
|
из
5.00
|
Выбор электродвигателя
Основными исходными данными для выбора электродвигателя являются:
- мощность на выходном вала  =2,8 Квт;
=2,8 Квт;
- частота вращения выходного вала  = 300 об/мин.
= 300 об/мин.
Требуемая мощность электродвигателя  =2,9кВт
=2,9кВт
где 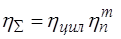 – общий КПД редуктора;
– общий КПД редуктора;
 – число пар подшипников. m=2
– число пар подшипников. m=2
В дальнейшем, поскольку в приводе отсутствуют дополнительные передачи, то  , где
, где  – передаточное число зубчатой передачи.
– передаточное число зубчатой передачи.
Рекомендуемые значения КПД зубчатой передачи  , подшипников
, подшипников  приведены в таблице 2.
приведены в таблице 2.
Таблица 2.
КПД зубчатой передачи, подшипников
| Элементы передач | Среднее значение 
|
| Зубчатая передача | 0,96…0,98 |
| Подшипники качения (одна пара) | 0,99 |
Частота вращения вала электродвигателя:
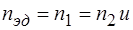 =300*3,15=945.
=300*3,15=945.
Номинальная мощность электродвигателя должна быть
 .
.
Номинальная мощность – это мощность, которую электродвигатель может отдавать длительно, не нагреваясь свыше допустимой температуры.
В общем машиностроении используются трехфазные асинхронные короткозамкнутые двигатели серии 4А (4 – порядковый номер серии; А – асинхронный). Номинальная мощность и частота вращения нашего двигателя 4А112MА6/955.
Для принятого электродвигателя в пояснительную записку заносят следующие параметры:
- обозначение двигателя;
- номинальную мощность  =3 кВт;
=3 кВт;
- частоту вращения при номинальной нагрузке  =955об/мин.
=955об/мин.
Кинематический и силовой расчет редуктора
Частота вращения валов:
- быстроходного принимаем  ;
;
- тихоходного принимаем  =300.
=300.
Угловые скорости вращения валов:
- входного  =3.14*955/30=99.9;
=3.14*955/30=99.9;
- выходного  =3.14*300/30=31.4.
=3.14*300/30=31.4.
Зависимости между вращающими моментами на валах используют при расчете передач:
 , следовательно,
, следовательно,  .
.
Крутящие моменты на валах при  :
:
-  =89.17/3.15=28.30– направление совпадает с направлением вращения вала, т.к. это момент движущих сил;
=89.17/3.15=28.30– направление совпадает с направлением вращения вала, т.к. это момент движущих сил;
-  =2800/31.4,2=89.17– его направление противоположно направлению вращения вала, т.к. это момент сил сопротивления.
=2800/31.4,2=89.17– его направление противоположно направлению вращения вала, т.к. это момент сил сопротивления.
Результаты проектирования заносят в таблицу 4.
Таблица 4.
Параметры редуктора
| Параметры | Вал 1 | Вал 2 |
| Частота вращения, об/мин |  =955 =955
|  =300 =300
|
| Угловая скорость, рад/с |  =99,9 =99,9
|  =31.4 =31.4
|
| Крутящий момент, Нм |  =28.30 =28.30
| 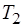 =89.17 =89.17
|
Расчет зубчатой передачи
Зубчатые передачи представляют собой механизм, передающий движение с помощью зубчатых колес (рисунок 2). Зубчатые колеса это тела (цилиндры) с равномерно расположенными выступами (зубьями) и впадинами.
Меньшее из зубчатых колес принято называть шестерней; большее – колесом. В нашем редукторе применяется косозубая передача внешнего зацепления (на рисунке ниже).

Определение допускаемых напряжений
Твердость зубчатых колес выбирают в зависимости от назначения и условий работы передачи. В курсовой работе применяются углеродистые и легированные стали, подвергнутые термической обработке, что позволяет обеспечивать требуемую твердость материала при заданной толщине заготовки.
Твердость используемого зубчатого колеса 223…262НВ и шестерни 262…311НВ.
2.2.2. Допускаемые напряжения в расчете на
контактную выносливость
| Этот вид расчета исключает усталостное выкрашивание рабочих поверхностей зубьев – основной вид разрушения поверхности зубьев для большинства закрытых быстроходных передах, работающих при хорошей смазке. |
Допускаемые контактные напряжения для пары сопрягаемых колес устанавливается следующим образом:
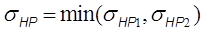 =(584;504)=504 МПа
=(584;504)=504 МПа
где  ,
,  ;
;
 =584.5
=584.5
 =504.5
=504.5
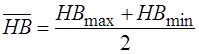 =(262+311)/2=286,5– среднее значение твердости для колеса;
=(262+311)/2=286,5– среднее значение твердости для колеса;
(223+262)/2=242,5 среднее значение твердости для шестерни.
 – коэффициент безопасности для однородной структуры материала.
– коэффициент безопасности для однородной структуры материала.
2.2.3. Допускаемые напряжения в расчете
на изгибную выносливость
Этот вид расчета исключает усталостную поломку зубьев. Определяют допускаемые напряжения раздельно для шестерни и колеса по формуле:

|  , МПа , МПа
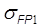 (шестерня)=295 МПа (шестерня)=295 МПа
 (колесо)=250 МПа
где (колесо)=250 МПа
где 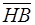 – среднее значение твердости; – среднее значение твердости;
 – коэффициент безопасности. – коэффициент безопасности.
|
2.3. Проектировочный расчет косозубой
зубчатой передачи
Цель расчета: определение межосевого расстояния и других параметров передачи, исключающих выкрашивание рабочей поверхности зубьев в работающей зубчатой паре.
Ориентировочное значение межосевого расстояния
 =
=  =84.5 мм
=84.5 мм
где 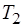 – крутящий момент на колесе, Н м;
– крутящий момент на колесе, Н м;
 – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии
– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии
 – коэффициент относительной ширины колеса для любых колес при симметричном расположении относительно опор.
– коэффициент относительной ширины колеса для любых колес при симметричном расположении относительно опор.
По ГОСТ 2185-66 принимаю межосевое расстояние (  ) 90мм
) 90мм
Модуль передачи  m=(0.01…0.02)=1.75мм ,
m=(0.01…0.02)=1.75мм ,
который округляют до ближайшего стандартного значения.
Стандартный ряд (выборка) модулей

| 1-й ряд | 1,25 | 1,5 | 2,5 | ||||||
| 2-й ряд | 1,75 | 2,25 | 2,75 | 3,5 | 4,5 | 5,5 |
Все параметры зацепления выражаются через модуль.
Ширина колеса определяется равенством:  ,мм.
,мм.
b2=38 мм
Ширина шестерни назначается  , мм.
, мм.
b1 По ГОСТ 6636-69 принимаю ширину 40 мм
Устанавливают угол наклона зуба:  .
.
Βmin=arcsin(7/38)=10.6
Минимальный угол наклона зуба  .
.
Затем определяют:
- суммарное число зубьев передачи  принимая в качестве
принимая в качестве  целую часть числа
целую часть числа 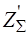 ;
;
- число зубьев шестерни 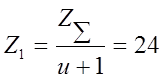 , округляя
, округляя 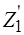 до целого числа
до целого числа  ;
;
- число зубьев колеса  .
.
Уточняют значение угла наклона зубьев


Уточняют фактическое передаточное число 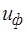 и его отклонение от заданного:
и его отклонение от заданного:
 ,
,  .
. 
Производится расчет геометрических параметров зубчатых колес по формулам, приведенным в таблице 7.
Таблица 7.
Расчет геометрических размеров зубчатых колес
| Наименование параметра | Обозначение | Формула | |
| 1. Делительный диаметр, мм | шестерни | 
| 
|
| колеса | 
| 
|
| 2. Межосевое расстояние, мм | 
| 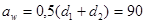
| |
| 3. Диаметр вершин зубьев, мм | шестерни | 
| 
|
| колеса | 
| 
| |
| 4. Диаметр впадин зубьев, мм | шестерни | 
| 
|
| колеса | 
| 
|
2.3.1. Проверочный расчет зубчатой передачи
на выносливость при изгибе
Для исключения усталостной поломки зубьев необходимо сопоставить расчетное местное напряжение  от изгиба в опасном сечении на переходной поверхности и допускаемые напряжения
от изгиба в опасном сечении на переходной поверхности и допускаемые напряжения 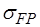 :
:
 .
.
Данное условие проверяют раздельно для шестерни и колеса. Расчетное местное напряжение при изгибе определяется по формуле:
- для колеса  МПа
МПа
- для шестерни 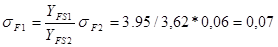 ,
,
где 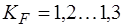 – коэффициент нагрузки при изгибе;
– коэффициент нагрузки при изгибе;

YFS1=3,47+13,2/26.11=3.975
YFS2=3,47+13,2/82.7=3,629 – коэффициент, учитывающий форму зуба и концентрацию напряжений;
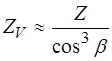
ZV1=24/0.918=26.11
ZV2=76/0.918=82.70 – эквивалентное число зубьев;
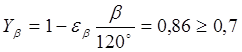 – коэффициент, учитывающий наклон зуба;
– коэффициент, учитывающий наклон зуба;  .
.
|
из
5.00
|
Обсуждение в статье: Определение допускаемых напряжений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

