 |
Главная |
Определение класса механизма
|
из
5.00
|
Выполним замену кинематических пар 4 класса путём введения заменяющих звеньев, которые образуют кинематические пары 5 класса. Схема заменяющего механизма представлена на рисунке 2.

Рисунок 2 – схема заменяющего механизма.
Выполним проверку произведённой замены.

Следовательно, замена выполнена верно.
Выделяем из состава механизма 1 класса.
W2
Оставшуюся ведомую цепь разбиваем на структурные группы. Разбивку проводим по сложным звеньям или сложным шарнирам. Эскизы структурных групп представлены на рисунке 3.
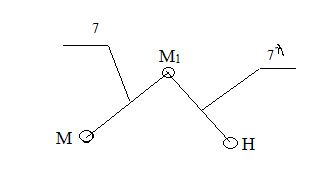
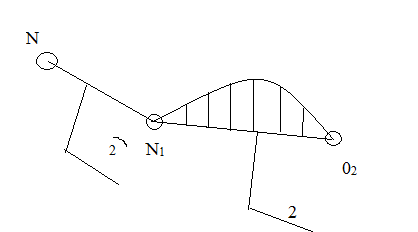
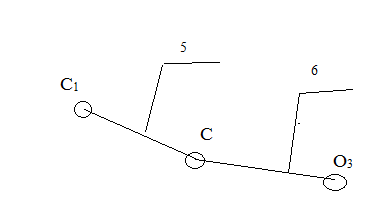
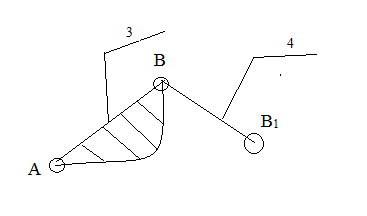
Рисунок 3 – эскизы структурных групп.
Так как в состав механизма кроме начального (механизма I класса) входят структурные группы только II класса, то весь механизм в целом относится к механизму II класса. Следовательно, при дальнейшем исследовании будем использовать методы, соответствующие данному классу механизмов.
Формула строения механизма
Гр. II кл.(7;7).
Механизм II кл. = механизм I кл.
Гр II кл.(2;2)
Гр.II кл.(3;4) гр. II кл. (5;6).
Кинематический анализ
Целью кинематического анализа является определение перемещений, скоростей и ускорений звеньев механизма и отдельных его точек без учёта сил. При этом задана схема и закон движения звеньев механизма. Кинематический анализ проводим для ведомой части механизма (звенья 2-6).
2.1. Совмещённый план положений (СПП)
Выполним построение СПП для шести положений звеньев механизма. Нумерацию положений выполним с одного из крайних.
Масштаб СПП определим по формуле:
 , где
, где
LO  A = 0.3 м
A = 0.3 м
- действительная длина кривошипа;
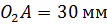 - отрезок, изображающий кривошип на чертеже.
- отрезок, изображающий кривошип на чертеже.
Подставляя известные значения, получим:
µ l= 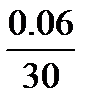 = 0.002 м/мм. .
= 0.002 м/мм. .
Размеры остальных звеньев и отрезков на чертеже будут равны:
O2A= 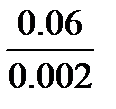 =30мм
=30мм
AB= 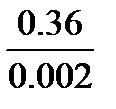 =180 мм
=180 мм
BC= 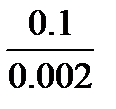 =50 мм
=50 мм
O3D= 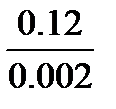 =60
=60
O3C= 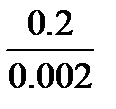 =100мм
=100мм
e=  =2.5 мм
=2.5 мм
x= 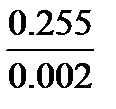 =127.5мм
=127.5мм
y= 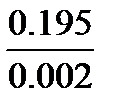 =97.5мм
=97.5мм
Используя построенный СПП выполним построение графика пути точки B как функцию 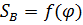 . Масштаб графика пути по оси ординат принимаем
. Масштаб графика пути по оси ординат принимаем  . Масштаб графика по оси абсцисс, то есть угла поворота кривошипа, определяется как:
. Масштаб графика по оси абсцисс, то есть угла поворота кривошипа, определяется как:
µφ=  , где
, где
X0-12=120мм - произвольно принятый отрезок по оси Х.
Тогда . µφ= 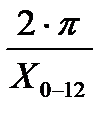 =
=  =0.052 рад/мм.
=0.052 рад/мм.
µt= 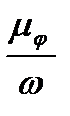 ,где ϖ-угловая скорость вращения ведущего звена. В данном случае ϖ2.Из формулы передаточного отношения U1-2= n1/n2.
,где ϖ-угловая скорость вращения ведущего звена. В данном случае ϖ2.Из формулы передаточного отношения U1-2= n1/n2.
Найдем частоту вращения звена 2.
n2 = 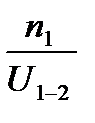 =
= 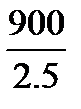 =360 об/мин.
=360 об/мин.
Из зависимости ϖ2=  найдем ϖ2.
найдем ϖ2.
ϖ2= 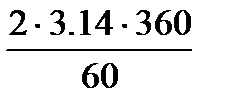 =37.68 с-1,
=37.68 с-1,
µt= 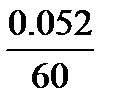 =0.001 c/мм.
=0.001 c/мм.
µs=0.004 м/мм.
Графически дифференцируя диаграмму перемещений, строим диаграмму скоростей точки B. Масштаб диаграммы скоростей равен:
µv= 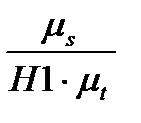 =
=  = 0.16м/c·мм, где
= 0.16м/c·мм, где
Аналогично, графически дифференцируем диаграмму скоростей для построения диаграммы ускорений. Масштаб диаграммы ускорений равен:
, где 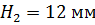 – произвольно выбранное полюсное расстояние.
– произвольно выбранное полюсное расстояние.
µа= 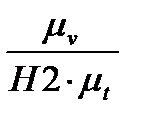 =
= 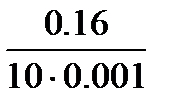 =16м/c2·мм
=16м/c2·мм
План скоростей
Скорость точки A определим по формуле:
VA=ϖ2·r=0.3·37.68=11.3м/c.
Из точки P, принятой за полюс плана скоростей, откладываем перпендикулярно к  в соответствии с направлением угловой скорости
в соответствии с направлением угловой скорости 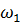 вектор скорости точки A. Длину вектора
вектор скорости точки A. Длину вектора  выбираем так, чтобы построение плана скоростей получилось чётким и наглядным.
выбираем так, чтобы построение плана скоростей получилось чётким и наглядным.
Пусть длина PVa=60 . Тогда масштаб плана скоростей равен:
µv=  =
=  =0.18 м/с·мм.
=0.18 м/с·мм.
Положение точки B на плане скоростей находи, решая систему векторных уравнений:
 , где
, где
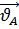 – известный по величине и направлению вектор скорости точки A;
– известный по величине и направлению вектор скорости точки A;
 – неизвестный по величине, но известный по направлению вектор скорости точки B относительно точки A, направленный перпендикулярно звену AB;
– неизвестный по величине, но известный по направлению вектор скорости точки B относительно точки A, направленный перпендикулярно звену AB;
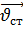 – вектор скорости точки, принадлежащей стойке и равный нулю;
– вектор скорости точки, принадлежащей стойке и равный нулю;
 – неизвестный по величине, но известный по направлению вектор скорости точки B относительно стойки, направленный параллельно направляющей.
– неизвестный по величине, но известный по направлению вектор скорости точки B относительно стойки, направленный параллельно направляющей.
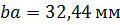 , отсюда
, отсюда 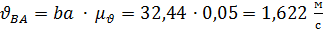 ;
;
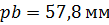 , отсюда
, отсюда 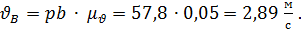
Положение точки C на плане скоростей найдём по изображающему свойству плана из соотношения:
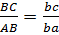 , отсюда
, отсюда 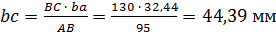 .
.
Скорость точки C относительно точки B:
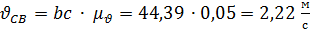 .
.
Скорость точки C:
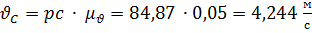 .
.
Положение точки D на плане скоростей находи, решая систему векторных уравнений:
 , где
, где
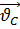 – известный по величине и по направлению вектор скорости точки C;
– известный по величине и по направлению вектор скорости точки C;
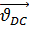 – неизвестный по величине, но известный по направлению вектор скорости точки D относительно стойки;
– неизвестный по величине, но известный по направлению вектор скорости точки D относительно стойки;
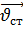 – вектор скорости точки, принадлежащей стойке, который равен нулю;
– вектор скорости точки, принадлежащей стойке, который равен нулю;
 – неизвестный по величине, но известный по направлению вектор скорости точки D относительно стойки.
– неизвестный по величине, но известный по направлению вектор скорости точки D относительно стойки.
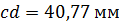 , отсюда
, отсюда 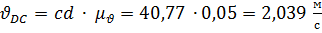 ;
;
 , отсюда
, отсюда 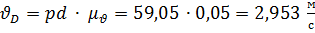 .
.
Положение точки E на плане скоростей найдём по изображающему свойству плана из соотношения:
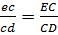 , отсюда
, отсюда 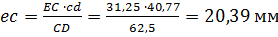 .
.
Из векторного уравнения 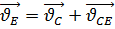 длина вектора
длина вектора 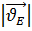 равна:
равна:
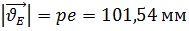 , отсюда
, отсюда 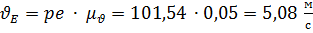 .
.
Пользуясь планом скоростей, определяем угловые скорости звеньев.
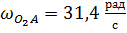 - угловая скорость кривошипа
- угловая скорость кривошипа  ;
;
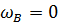 , так как шатун B движется возвратно-поступательно;
, так как шатун B движется возвратно-поступательно;
 - угловая скорость звена BC;
- угловая скорость звена BC;
 - угловая скорость звена CD;
- угловая скорость звена CD;
 - угловая скорость кривошипа
- угловая скорость кривошипа 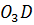 .
.
План ускорений
Порядок получения точек на плане ускорений аналогичен тому, как эти точки определялись на плане скоростей. Ускорение точки A будет обладать только нормальным ускорением, величина которого равна:
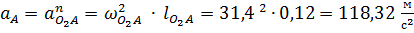 .
.
Тогда масштаб плана ускорений будет равен:
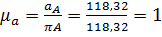 , где
, где 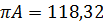 мм – отрезок произвольной длины.
мм – отрезок произвольной длины.
Направлен вектор  параллельно звену
параллельно звену  из точки A в точку
из точки A в точку  .
.
Решая систему векторных уравнений, найдём на плане ускорений положение точки B:
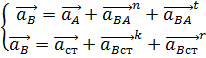 , где
, где
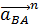 – нормальное ускорение точки B во вращательном движении звена AB относительно точки A, которое по модулю равно:
– нормальное ускорение точки B во вращательном движении звена AB относительно точки A, которое по модулю равно:
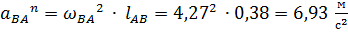 .
.
Длина отрезка  равна:
равна:
 мм .
мм .
 – касательное ускорение точки B относительно точки A, направленное перпендикулярно к линии AB и по модулю неизвестное;
– касательное ускорение точки B относительно точки A, направленное перпендикулярно к линии AB и по модулю неизвестное;
 – вектор ускорения точки, принадлежащей стойке, который равен нулю;
– вектор ускорения точки, принадлежащей стойке, который равен нулю;
 – кориолисово ускорение точки B в движении её относительно относительно точки, принадлежащей стойке, которое равно нулю, так как направляющая этой стойки неподвижна;
– кориолисово ускорение точки B в движении её относительно относительно точки, принадлежащей стойке, которое равно нулю, так как направляющая этой стойки неподвижна;
 – релятивное ускорение точки B относительно точки, принадлежащей стойке, параллельно направляющей стойки.
– релятивное ускорение точки B относительно точки, принадлежащей стойке, параллельно направляющей стойки.
 , отсюда
, отсюда  ;
;
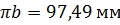 , отсюда
, отсюда 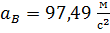 ;
;
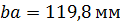 , отсюда
, отсюда 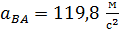 – полное ускорение точки B относительно точки A.
– полное ускорение точки B относительно точки A.
Положение точки C на плане ускорений найдём по изображающему свойству плана из соотношения:
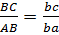 , отсюда
, отсюда 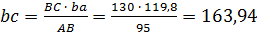 мм .
мм .
Ускорение точки C относительно точки B равно:
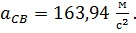
Ускорение точки C равно:
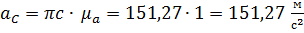 .
.
Решая систему векторных уравнений, найдём на плане ускорений положение точки D:
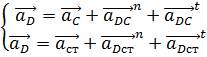 , где
, где
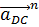 - нормальное ускорение точки D во вращательном движении звена DC относительно точки C, которое по модулю равно:
- нормальное ускорение точки D во вращательном движении звена DC относительно точки C, которое по модулю равно:
 .
.
Длина отрезка 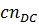 равна:
равна:
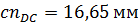 .
.
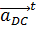 - касательное ускорение точки D относительно точки C, направленное перпендикулярно к линии DC и по модулю неизвестное;
- касательное ускорение точки D относительно точки C, направленное перпендикулярно к линии DC и по модулю неизвестное;
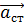 – вектор ускорения точки, принадлежащей стойке, который равен нулю;
– вектор ускорения точки, принадлежащей стойке, который равен нулю;
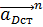 - нормальное ускорение точки D во вращательном движении звена
- нормальное ускорение точки D во вращательном движении звена 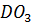 относительно точки, принадлежащей стойке, которое по модулю равно:
относительно точки, принадлежащей стойке, которое по модулю равно:
 .
.
Длина отрезка 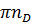 равна:
равна:
 .
.
 – касательное ускорение точки D относительно точки, принадлежащей стойке, направленное перпендикулярно к звену
– касательное ускорение точки D относительно точки, принадлежащей стойке, направленное перпендикулярно к звену 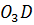 и неизвестное по модулю.
и неизвестное по модулю.
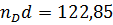 мм , отсюда
мм , отсюда  ;
;
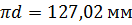 , отсюда
, отсюда 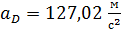 ;
;
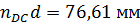 , отсюда
, отсюда  ;
;
 , отсюда
, отсюда 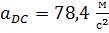 – полное ускорение точки D относительно точки C.
– полное ускорение точки D относительно точки C.
Положение точки E на плане ускорений найдём по изображающему свойству плана из соотношения:
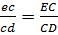 , отсюда
, отсюда  .
.
Из векторного уравнения 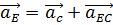 длина вектора
длина вектора 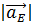 равна:
равна:
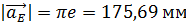 , отсюда
, отсюда  .
.
Определим нормальное и касательное ускорения точки E относительно точки C:
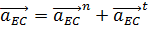 , где
, где
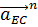 – нормальное ускорение точки E во вращательном движении звена CE относительно точки C, которое по модулю равно:
– нормальное ускорение точки E во вращательном движении звена CE относительно точки C, которое по модулю равно:
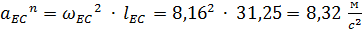 .
.
Длина отрезка  равна:
равна:
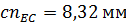 .
.
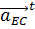 – касательное ускорение точки E относительно точки C, направленное перпендикулярно к линии CE и по модулю неизвестное.
– касательное ускорение точки E относительно точки C, направленное перпендикулярно к линии CE и по модулю неизвестное.
 , отсюда
, отсюда 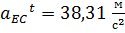 .
.
Пользуясь построенным планом ускорений, определяем угловые ускорения звеньев.
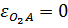 , так как угловая скорость кривошипа
, так как угловая скорость кривошипа  постоянна.
постоянна.
 , так как ползун образует поступательную пару с неподвижной направляющей стойки.
, так как ползун образует поступательную пару с неподвижной направляющей стойки.
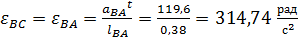 – угловое ускорение звена BC;
– угловое ускорение звена BC;
 – угловое ускорение звена DE;
– угловое ускорение звена DE;
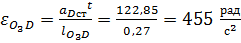 – угловое ускорение звена
– угловое ускорение звена 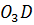 .
.
|
из
5.00
|
Обсуждение в статье: Определение класса механизма |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

