 |
Главная |
Спектральная плотность входного сигнала
|
из
5.00
|
РАССЧИТЫВАЕМЫЕ ХАРАКТЕРИСТИКИ
1. Корреляционная функция для входного сигнала.
2. Спектральная плотность входного сигнала, амплитудный и фазовый спектр, ширина спектра.
3. Частотный коэффициент передачи цепи, АЧХ, ФЧХ.
4. Импульсная и переходная характеристики цепи.
5. Спектральная плотность выходного сигнала, амплитудный и фазовый спектр, ширина спектра.
6. Выходной сигнал.
ИСХОДНЫЕ ДАННЫЕ
Схема электрическая принципиальная:

Входной сигнал:
 | ||||
| ||||
| ||||
Параметры элементов цепи и сигнала:
| Вариант | Параметры | |
| C C1,нФ | ||
| C C2,нФ | ||
| L L1 мГн | ||
| L L2,мГн | ||
| R1,кОм | ||
| R2,кОм | ||
| U,В | ||
| Е T,мкс |
1. Нахождение корреляционной функции для входного сигнала, сдвинутого на  на интервале
на интервале 
При обработке сигналов часто приходится сравнивать сигнал со смещёнными во времени копиями этого сигнала, а также другими сигналами. О степени связи сигнала со смещёнными копиями можно судить по корреляционным функциям. Для вещественного сигнала S(t), имеющего конечную энергию на бесконечном интервале времени автокорреляционная функция определяется следующим образом:
 (1.1)
(1.1)
где  -интервал сдвига функции.
-интервал сдвига функции.
При таком определении автокорреляционная функция (АКФ) имеет размерность энергии.
В нашем случае мы имеем сигнал треугольной формы, представленный на рис 1.1.
|
 |
Рис.1.1 Исходный сигнал.
Математически исходный сигнал можно записать:

|
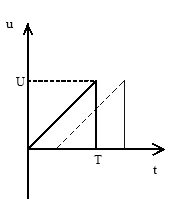
Рис.1.2 Смещенный во времени сигнал

Корреляционная функция для входного сигнала, сдвинутого на  на интервале [τ, T], согласно (1.1) определяется следующим образом:
на интервале [τ, T], согласно (1.1) определяется следующим образом:
 (1.2)
(1.2)
где s (  ) - единичная функция
) - единичная функция
График корреляционной функции (1.2) представлен на рис.1.3

Рис.1.3 Корреляционная функция входного сигнала
Нахождение интервала корреляции:
 (1.3)
(1.3)
 (1.4)
(1.4)
 (1.5)
(1.5)
Подставляя (1.4) и (1.5) в (1.3), найдем значение интервала корреляции:
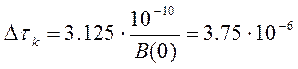
Спектральный анализ входного сигнала
Спектральная плотность входного сигнала
 (2.1.1)
(2.1.1)
Данная функция является спектральной плотностью сигнала s(t). Формула (2.1.1) осуществляет преобразование Фурье данного сигнала. Спектральная плотность - комплекснозначная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе элементарных синусоид. Модуль спектральной плотности есть амплитудный спектр сигнала, а ее аргумент - фазовый спектр.
Запишем математическое выражение для входного сигнала, используя единичную функцию 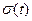 :
:
 (2.1.2)
(2.1.2)
График входного сигнала представлен на рис. 2.1

Рис.2.1 Входной сигнал
Представим сигнал в операторной форме. При нахождении изображения сигнала по Лапласу необходимо учитывать свойство временного сдвига:
 (2.1.3)
(2.1.3)
При этом изображения простых сигналов определяются как:
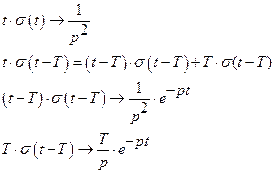 (2.1.4)
(2.1.4)
Применяя свойство линейности и временного сдвига (2.1.3), а также, учитывая (2.1.4) найдем изображение нашего сигнала:
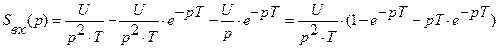 (2.1.5)
(2.1.5)
Так как площадь фигуры, ограниченной графиком функции s(t) и осью абсцисс, является конечной величиной, сигнал s(t) – абсолютно интегрируемый, следовательно, для перехода от изображения к спектральной плотности достаточно заменить p на jω.
Заменив p на jω, получим:
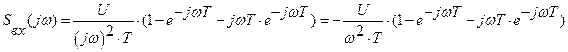
Для преобразования используем формулу Эйлера (2.1.6):
 (2.1.6)
(2.1.6)
Тогда

 (2.1.7)
(2.1.7)
|
из
5.00
|
Обсуждение в статье: Спектральная плотность входного сигнала |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

