Случайные процессы и величины

Глава I. Элементы теории вероятностей.

 

Большинство разделов физики оперируют достаточно неболь-шим количеством объектов и связей между ними. При описании же процессов, происходящих в веществе, мы вынуждены рассматри-вать огромное количество объектов – молекул. Реальное вещество состоит из очень большого количества молекул. Например, в обыч-ном состоянии в 12 граммах изотопа углерода содержится N=6,02^.10²³ молекул (число Авогадро). С точки зрения обычной механики, для каждой молекулы надо было бы записать уравнение движения:

, где (1.1)

 

Более того, для решения системы из N векторных уравнений необходимо будет записать эти уравнения в проекциях сил на 3 оси координат. Итого, для N молекул мы запишем 3N уравнений. Ре-шать такое количество уравнений совместно невозможно даже с применением современной вычислительной техники. Время реше-ния подобной системы уравнений во много раз превышает время, за которое рассматриваемая система молекул изменит свое состоя-ние. Отсюда видно, что для описания большого коллектива частиц невозможно пользоваться динамическим методом. Для описания таких коллективов прибегают к статистическому (вероятностному) и термодинамическому методам.

Основной особенностью статистических методов является их вероятностный характер: рассматриваемый процесс представляется как процесс случайный, и выводятся некоторые закономерности для него.

На практике часто приходится сталкиваться со случайными про-цессами. Случайность – это неустановленная закономерность. И в большинстве случаев бывает гораздо выгоднее статистически опи-сать случайный процесс, нежели определять закономерность полу-чения того или иного результата и учитывать всю совокупность параметров, приводящих к конкретному результату.

Случайным процессом называется такой процесс, который при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по–иному. Например, к случайным процес-сам можно отнести бросание монеты или игральной кости. Каждый из этих процессов безусловно подчиняется хорошо известным фи-зическим законам. Вместе с тем, описать каждый конкретный слу-чай достаточно сложно – он зависит от очень большого количества условий. Поэтому процесс можно считать случайным.

Каждому случайному процессу можно поставить в соответствие случайную величину, характеризующую этот процесс. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем заранее неизвестно, какое именно. Случайные величины разделяются на дискретные, возмож-ные значения которых могут быть заранее просчитаны, и непрерыв-ные, непрерывно заполняющие некоторый промежуток. В нашем примере с монетой случайная величина, описывающая процесс бросания, может принимать два значения: или Р(решетка) или О(орел). Случай, когда монета встает на ребро, происходит очень редко, поэтому учитывать его не будем. Для математического опи-сания случайной величины лучше присваивать ей численные значе-ния, скажем, 0 для решетки, и 1 для орла. В примере с игральной костью за случайную величину удобно принять количество очков, выпавших при бросании. Случаи, когда кость встает на ребро или на вершину, также не учитываются.

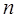Статистической вероятностью появления определенного значения случайной величины называется отношение коли-чества появлений данного значения случайной величины к общему количеству проведенных опытов:

 

(1.2)

 

Статистическая вероятность является величиной оценочной, приблизительной. Она рассчитывается по ограниченному количест-ву опытов. Если провести опыт с бросанием монеты 10 раз 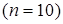, то можно получить результат, при котором решетка выпадет 7 раз . Отсюда статистическая вероятность выпадения решетки Это значение достаточно далеко от истинного (при условии, что обе стороны монеты равноправны). Для получе-ния более точных характеристик необходимо увеличить количество опытов и рассчитать вероятность появления решетки. При доста-точно большом количестве опытов станет ясно, что вероятность выпадения орла равна вероятности выпадения решетки. Обе эти вероятности имеют одно и то же значение: .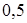

Вероятностью появления определенного значения назы-вается предел статистической вероятности при стремлении коли-чества опытов к бесконечности:

 

(1.3)

 

Событием называется всякий факт, который в результате прове-дения опыта может произойти или может не произойти.

Несовместными событиями называются события, которые не могут произойти одновременно в результате одного опыта. Напри-мер, невозможно выпадение и орла и решетки одновременно.

Независимыми событиями называются такие события, возник-новение которых не зависит друг от друга.

Для несовместных и независимых событий можно сформулиро-вать следующие свойства вероятностей:

1. Вероятность того, что произойдет хотя бы одно из событий или равна сумме вероятностей происхождения этих событий:

 

(1.4)

 

2. Вероятность того, что сразу после события 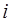произойдет со-бытие , равна произведению вероятностей происхождения этих событий:

(1.5)

 

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значе-ниями случайной величины и соответствующими им вероятностя-ми.

 

ФУНКЦИЯ И ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ

 

Для количественной характеристики распределения вероят-ностей удобней пользоваться не вероятностью того события, что случайная величина примет значение ,т.е. , а ве-роятностью события , т.е. того, что случайная величина примет значение, меньшее некоторой текущей переменной . Вероятность этого события зависит от значения , т.е. является функцией от . Эта функция называется функцией распределения
случайной величины и обозначается :

 

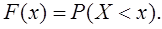(1.6)

 

Функция распределения случайной величины ¾ самая универ-сальная характеристика случайной величины, она существует как для дискретных случайных величин, так и для непрерывных. Функ-ция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Функции распределения обладают некоторыми об-щими свойствами:

1. Функция распределения есть неубывающая функция сво-его аргумента, т.е. при выполняется .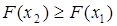

2. На минус бесконечности функция распределения равна нулю: .

3. На плюс бесконечности функция распределения равна едини-це: .

График функции распределения в общем случае может быть представлен как график неубывающей функции (рис.1), значения которой начинаются от 0 и доходят до 1, причем в отдельных точ-ках функция может иметь скачки (разрывы).

 

Пусть имеется непрерывная случайная величина с функцией распределения , которую мы предположим непрерывной и дифференцируемой. Поскольку для непрерывной случайной величи-ны вероятность принятия случайной величиной любого отдельного значения равна нулю, то вычислим вероятность попадания этой
случайной величины на участок от до :

 

(1.7)

 

Вероятность попадания в указанный интервал рассчитывается как приращение функции распределения на этом участке. Рассмот-рим отношение этой вероятности к величине интервала, т.е. сред-нюю вероятность, приходящуюся на единицу длины на этом участ-ке, и будем приближать 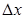к нулю. В пределе получим производ-ную от функции распределения:

 

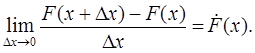(1.8)

 

Введем обозначение для производной от функции распределе-ния:

(1.9)

 

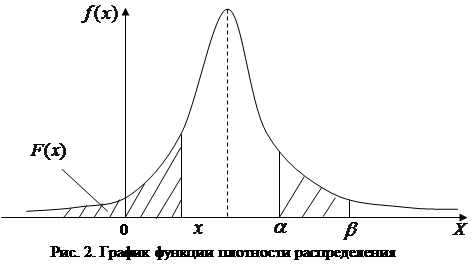Функция характеризует как бы плотность, с которой рас-пределяется значение случайной величины в данной точке (а на самом деле отражает быстроту возрастания функции распределе-ния). Функция называется плотностью распределения (или плотностью вероятности) непрерывной случайной величины . В отличие от функции распределения, плотность распределения не является универсальной – она существует только для непрерывных величин. Кривая, изображающая плотность распределения случай-ной величины, называется кривой распределения (рис.2).

Геометрически вероятность попадания величины в участок равна площади кривой распределения,опирающейся на этот участок. Значение же функции распределения есть не что иное, как площадь кривой распределения, лежащей левее точки .

Для дискретных величин аналогом графика распределения может служить гистограмма, отображающая величину прироста функции распределения (рис.3).

 

Плотность распределения обладает следующими свойствами:

1. Плотность распределения есть неотрицательная функция: . Это свойство вытекает непосредственно из того, что есть функция неубывающая.

2. Интеграл в бесконечных пределах от плотности вероятности равен единице: (условие нормировки). Условие говорит о том, что вероятность принятия случайной величиной какого–ли-бо значения равна единице.

 

 

ПАРАМЕТРЫ ЗАКОНА РАСПРЕДЕЛЕНИЯ

 

Каждый закон распределения представляет собой некоторую функцию, и указание этой функции полностью описывает случай-ную величину с вероятностной точки зрения. Однако на практике часто нет необходимости характеризовать случайную величину полностью, достаточно указать отдельные числовые параметры, до некоторой степени характеризующие существенные черты распре-деления случайной величины, например, какое–то среднее значе-ние, какое–либо число, характеризующее степень разбросанности значений случайной величины относительно среднего.

Основной характеристикой случайной величины является мате-матическое ожидание, которое иногда называют просто средним значением случайной величины. Рассмотрим дискретную случай-ную величину , принимающую значения с вероят-ностями, соответственно, 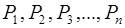. Для того чтобы охаракте-ризовать каким–то числом положение значения случайной величи-ны на оси абсцисс с учетом того, что эти значения имеют различ-ные вероятности, удобно воспользоваться так называемым “сред-ним взвешенным” из значений , причем каждое значение 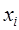при осреднении должно учитываться с “весом”, пропорциональным ве-роятности этого значения. Вычисленное среднее значение 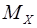бу-дет называться математическим ожиданием случайной величины :

 

(1.10)

 

Поскольку сумма вероятностей всех возможных значений слу-чайной величины равна единице ( ), если события несов-местные, то математическое ожидание рассчитывается по формуле:

 

(1.11)

 

Итак, математическим ожиданием называется сумма произведе-ний всех возможных значений случайной величины на вероятности этих значений. Для непрерывных случайных величин математи-ческое ожидание определяется по формуле:

 

(1.12)

 

Математическое ожидание случайной величины относится к так называемым начальным моментам случайной величины, характе-ризующим положение случайной величины. Начальным моментом -го порядка случайной величины называется сумма вида:

 

(1.13)

 

для дискретных случайных величин; и

 

(1.14)

 

для непрерывных случайных величин.

Таким образом, математическое ожидание является начальным моментом первого порядка или первым начальным моментом. Оче-видна физическая интерпретация математического ожидания: если на оси в точках 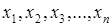располагаются массы , то первый начальный момент определит положение центра масс на оси . Для пространственного случая будет определено положение центра масс в пространстве относительно точки начала отсчета.

Пользуясь определением математического ожидания, можно дать следующее определение начального момента: начальным мо-ментом -го порядка случайной величины называется математи-ческое ожидание -й степени этой случайной величины:

 

(1.15)

 

Другими важными характеристиками распределения случайной величины являются так называемые центральные моменты.

Назовем отклонением (или флуктуацией) случайной величи-ны разность между значением случайной величины и ее матема-тическим ожиданием:

(1.16)

 

Другое название флуктуации случайной величины – это цен-трированная случайная величина, соответствующая величине . Центрирование случайной величины равносильно переносу начала координат в точку, координата которой равна математическому ожиданию.

Моменты центрированной случайной величины носят название центральных моментов. Они равносильны моментам относитель-но центра масс в механике.

Таким образом, центральным моментом –го порядка случай-ной величины называется математическое ожидание –й степе-ни соответствующей центрированной величины:

 

(1.17)

 

Для дискретной случайной величины –й центральный момент выражается суммой:

, (1.18)

 

а для непрерывной- интегралом:

 

(1.19)

 

Для любой случайной величины первый центральный момент равен нулю:

, (1.20)

 

так как математическое ожидание центрированной случайной величины всегда равно нулю.

Большое значение для характеристики распределения случайной величины имеет второй центральный момент, называемый диспер-сией 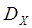случайной величины, который представляет собой мате-матическое ожидание квадрата отклонения случайной величины:

 

(1.21)

 

для дискретных случайных величин;

 

(1.22)

 

для непрерывных случайных величин.

Дисперсия случайной величины характеризует рассеяние значе-ний случайной величины относительно математического ожидания. Механическая интерпретация второго центрального момента (дис-персии) – это момент инерции тела относительно центра масс.

Для наглядной характеристики рассеивания случайной величи-ны удобней пользоваться величиной, размерность которой совпада-ет с размерностью самой случайной величины. Для этого из дис-персии извлекают квадратный корень, и полученная величина но-сит название среднего квадратичного отклонения случайной вели-чины :

(1.23)

 

Для характеристики асимметрии распределения используют тре-тий центральный момент, он имеет размерность куба случайной ве-личины; чтобы получить безразмерную величину, его делят на куб среднего квадратичного отклонения :

 

(1.24)

 

Полученная величина называется коэффициентом асимметрии или просто асимметрией.

Четвертый центральный момент характеризует остро- или плос-ковершинность распределения. Соответствующий коэффициент на-зывается эксцессом и рассчитывается как

 

(1.25)

 

Число 3 вычитается потому, что для самого распространенного в природе нормального закона, который мы рассмотрим позже, от-ношение . Таким образом, для нормального закона эксцесс равен нулю; более островершинные законы будут иметь положи-тельный эксцесс, более плосковершинные – отрицательный.

 

ПРИМЕРЫ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ

 

Самым простым законом распределения является закон равномерного распределения, при котором все возможные значения случайной величины равновероятны. График функции распреде-ления при равномерном распределении представляет собой прямую линию (рис.4):

 

Основные характеристики равномерного распределения:

 

; ;

 

; ;

 

 

Наиболее часто встречающийся на практике закон распределе-ния – это нормальный закон распределения, который еще называют законом Гаусса. Главная особенность нормального закона, отлича-ющая его от других законов распределения, состоит в том, что нор-мальный закон является предельным законом, к которому прибли-жаются другие законы распределения при весьма часто встреча-ющихся типичных условиях.

Функция плотности распределения нормального закона имеет вид:

(1.26)

 

Основной особенностью графика плотности распределения по нормальному закону является то, что кривая распределения имеет симметричный холмообразный вид (рис.5).

Максимуму функции, равному , соответствует точка ; по мере удаления от точки плотность распределения падает, и при кривая асимптотически приближается к оси абсцисс. Численные параметры и , входящие в распределение, есть, со-ответственно, математическое ожидание и среднее квадратичное от-клонение. Непосредственно из формулы (1.26) видно, что явля-ется центром симметрии распределения. Это ясно из того, что при изменении знака разности выражение (1.26) не изменяется. График нормального распределения симметричен относительно ма-тематического ожидания. Если изменить параметр , то график будет смещаться, не изменяя своей формы вдоль оси абсцисс. То есть параметр характеризует положение распределения на оси абсцисс. Параметр же характеризует не положение, а форму кри-вой распределения. Это есть характеристика рассеивания. Наиболь-шая ордината кривой распределения обратно пропорциональна ; при увеличении максимальная ордината уменьшается. Так как площадь фигуры, ограниченной сверху кривой распределения, должна всегда быть равной единице, то при увеличении кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении кривая распределения вытягивается вверх, сжимаясь с боков, становясь более иглообразной.

На рис.6 показаны три нормальные кривые распределения при , для которых выполняется соотношение .

 

Математическое ожидание и дисперсия случайной величины для нормального распределения в общем виде раcсчитываются доста-точно сложно, и их конкретные значения зависят от конкретного вида случайной величины; но можно выяснить соотношения между средним квадратичным отклонением и центальными моментами. Эти соотношения не зависят от конкретного распределения, и для всех случайных величин, подчиняющихся нормальному закону, оди-наковы. Для нормального закона выполняется следующее соот-ношение между центральными моментами:

 

(1.27)

 

Так как 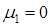, то все нечетные моменты также равны нулю. Это, впрочем, следует и из симметричности распределения. Так как для нормального закона , то его асимметрия также равна нулю:

(1.28)

 

Для четных моментов выполняются следующие соотношения:

 

; (1.29)

, (1.30)

 

отсюда имеем эксцесс для нормального закона

 

(1.31)

 

Глава II. Распределение Максвелла

 

Распределение Максвелла занимает особое место среди прочих законов распределения. Этот закон описывает скорости движения молекул газа, находящегося в термодинамическом равновесии. Распределение Максвелла является следствием нормального закона распределения. Распределение молекул по одной составляю-щей скорости описывается нормальным законом распределения:

 

, (2.1)

 

где 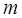– масса молекулы газа, 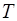– абсолютная температура,

– постоянная Больцмана.

Поскольку функция является экспоненциальной зависи-мостью от квадрата проекции скорости , то она является симмет-ричной относительно нулевого значения и график её совпадает с кривой Гауссовского распределения (рис. 7).

Вероятность того, что проекция скорости лежит в интервале равна площади заштрихованной полоски. Функция нормирована на единицу, т.е. площадь под кривой :

 

(2.2)

 

Интегрирование в бесконечных пределах не означает, что в газе есть молекулы с такими скоростями (скорость движения ограниче-на скоростью света). Молекул с очень большими скоростями доста-точно мало, и они не вносят никакого вклада в нормировочный ин-теграл. Это и позволяет записывать такие пределы интегрирования.

Аналогичный вид имеют выражения для функций по осям и ( ).

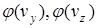Поскольку оси координат равноправны, как и равноправны проекции , то находим, что распределение по скоростям может быть найдено как:

 

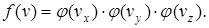(2.3)

 

Тогда для объемной функции распределения получаем (так как ):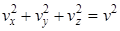

(2.4)

 

Объемная плотность распределе-ния позволяет найти вероятность по-падания модуля скорости молекул в определенный интервал. В отличие от площадь под кривой физического смысла не имеет.

Найдем вероятность или относи-тельное число молекул, модуль ско-рости которых заключен в интерва-ле . Таким молекулам соот-ветствуют точки в пространстве ско-ростей, попадающие в сферический слой с радиусами и (рис.8).

Объем этого слоя равен произведению поверхности слоя и его толщины, т.е. , объемная плотность вероятности во всех точках слоя одинакова. Попадание модулей скорости разных моле-кул в заданный слой есть события независимые, и мы можем при-менять свойство сложения вероятностей.

Вероятность попадания в этот слой:

 

(2.5)

 

Искомая зависимость вероятности от модуля скорости моле-кулы:

(2.6)

 

Учитывая выражение для объемной плотности вероятности и то, что скорость движения молекул зависит от температуры сре-ды, запишем закон распределения Максвелла по модулю скорости:

 

(2.7)

 

Эта функция также нормирована на единицу:

 

(2.8)

 

Следует обратить внимание, что в показателе экспоненты стоит взятое со знаком минус отношение кинетической энергии молекулы , соответствующей рассматриваемой скорости 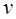, к величине , характеризующей среднюю энергию молекул газа. Функция зависит не только от скорости молекул, но и от температуры газа, что и отражено в обозначении функции.

Полученные Максвеллом распределения по скоростям не зави-сят ни от структуры молекул, ни от вида взаимодействия из друг с другом. Поэтому они применимы не только к газам, но и к другим агрегатным состояниям вещества, что мы и увидим в лабораторной работе №2.

Вид функции приведен на рис.9.

Характерные скорости

 

Полученные выражения для распределения по скоростям позво-ляют установить некоторые характеристики этого распределения. Это три скорости движения молекул газа: наиболее вероятная , средняя и среднеквадратичная .

Наиболее вероятной скорости соответствует максимум функции распределения , который находится из условия ра-венства нулю производной по скорости:

 

(2.9)

 

или, опуская постоянные множители:

 

(2.10)

 

Данному уравнению удовлетворяют три значения скорости:

1.

2. . Оба значения соответствуют минимумам .

3. Значение 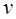, обращающее в нуль выражение , и дает нам искомую наиболее вероятную скорость:

 

, (2.11)

 

где - молярная масса газа.

Средняя скорость (имеется в виду средняя арифметическая скорость) по определению

 

(2.12)

Среднеквадратичная скорость находится из условия

 

, (2.13)

 

откуда

 

(2.14)

 

Поскольку функция распределения Максвелла несимметрична относительно наиболее вероятного значения, то и для трёх харак-терных скоростей значения различны. Вместе с тем наблюдается постоянное соотношение характерных скоростей:

 

(2.15)

 

Зависимость распределения от температуры

 

Подставив выражение для наиболее вероятной скорости в выражение для функции распределения , найдем максималь-ное значение :

 

(2.16)

 

Отсюда видно, что при увеличении температуры (при постоян-ной массе молекул) или уменьшении массы молекул(при постоян-ной температуре) максимум функции смещается в сторону больших скоростей, а величина максимума уменьшается. При этом площадь под кривой остается равной единице. Наглядно зависи-мость можно представить в виде трёх кривых, которые можно рас-сматривать как кривые функции для постоянной темпера-туры при либо для постоянной массы при (рис.10)