 |
Главная |
Пределы применимости классической теории твердого тела
|
из
5.00
|
В качестве примера применения квантовой статистики рассмотрим внутреннюю энергию кристаллического твердого тела. Расположение атомов в узлах кристаллической решетки отвечает минимуму их потенциальной энергии. При смещении атомов из положения равновесия в любом направлении появляется сила, стремящаяся вернуть его в первоначальное положение, вследствие чего возникают колебания атомов. Колебание вдоль произвольного направления можно представить как наложение колебаний вдоль трех взаимно перпендикулярных направлений. Поэтому каждому атому в кристалле следует приписать три колебательные степени свободы.
Как было ранее выяснено, на каждую колебательную степень свободы в среднем приходится энергия, равная двум половинкам kТ — одна в виде кинетической и одна в виде потенциальной энергии. Следовательно, на каждый атом приходится в среднем энергия, равная 3kT. Энергию моля вещества в кристаллическом состоянии можно найти, умножив среднюю энергию одной частицы на число частиц, размещенных в узлах кристаллической решетки. Последнее число совпадает с числом Авогадро NA только в случае химически простых веществ. В случае такого, например, вещества, как NaCl, число частиц будет равно 2NА, ибо в моле NaCl содержится NA атомов Na и NA атомов С1.
Ограничившись рассмотрением химически простых веществ, образующих атомные или металлические кристаллы, для внутренней энергии моля вещества в кристаллическом состоянии можно написать выражение
 .
.
Приращение внутренней энергии, соответствующее повышению температуры на один градус, равно теплоемкости при постоянном объеме. Следовательно,
 .
.
 Поскольку объем твердых тел при нагревании меняется мало, их теплоемкость при постоянном давлении незначительно отличается от теплоемкости при постоянном объеме, так что можно положить
Поскольку объем твердых тел при нагревании меняется мало, их теплоемкость при постоянном давлении незначительно отличается от теплоемкости при постоянном объеме, так что можно положить  и говорить просто о теплоемкости твердого тела.
и говорить просто о теплоемкости твердого тела.
 Итак, теплоемкость моля химически простых тел в кристаллическом состоянии одинакова и равна 3R. Это утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем. Закон выполняется с довольно хорошим приближением для многих веществ при комнатной температуре. Однако, например, алмаз имеет при комнатной температуре теплоемкость, равную всего примерно 0,7R.
Итак, теплоемкость моля химически простых тел в кристаллическом состоянии одинакова и равна 3R. Это утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем. Закон выполняется с довольно хорошим приближением для многих веществ при комнатной температуре. Однако, например, алмаз имеет при комнатной температуре теплоемкость, равную всего примерно 0,7R.
Более того, теплоемкость кристаллов зависит от температуры, причем зависимость имеет характер, показанный на рис. 4.1. Вблизи абсолютного нуля теплоемкость всех тел пропорциональна T 3, и только при достаточно высокой, характерной для каждого вещества температуре начинает выполняться закон Дюлонга и Пти. У большинства тел это достигается уже при комнатной температуре, у алмаза же теплоемкость достигает значения 3R лишь при температуре порядка 1000°С.
Таким образом, классическая теория теплоемкости кристаллов имеет границы своего применения, и при низких температурах необходимо квантовое рассмотрение. Применение квантовой теории позволило Эйнштейну уже в 1906 г. дать принципиальное объяснение падения теплоемкости кристаллов вблизи абсолютного нуля температуры. Эйнштейн рассматривал кристалл как совокупность N независимых гармонических осцилляторов, колеблющихся около положения равновесия с одной и той же частотой ω. В отличие от классического закона  распределения энергии по степеням свободы квантовая теория предполагает, что средняя энергия, приходящаяся на одну степень свободы, в этом случае определяется формулой Планка:
распределения энергии по степеням свободы квантовая теория предполагает, что средняя энергия, приходящаяся на одну степень свободы, в этом случае определяется формулой Планка:
 (4.1)
(4.1)
в которой опущен член  , представляющий нулевую энергию осциллятора. Этот член надо учитывать в тех вопросах, когда существенна амплитуда колебаний, например в вопросе зависимости рассеяния рентгеновских лучей от температуры. В вопросе о теплоемкости нулевая энергия роли не играет, поскольку она не зависит от температуры.
, представляющий нулевую энергию осциллятора. Этот член надо учитывать в тех вопросах, когда существенна амплитуда колебаний, например в вопросе зависимости рассеяния рентгеновских лучей от температуры. В вопросе о теплоемкости нулевая энергия роли не играет, поскольку она не зависит от температуры.
При высоких температурах формула (4.1) переходит в классическое выражение  , а поэтому в вопросе о теплоемкости приводит к закону Дюлонга и Пти. При низких температурах формула, полученная Эйнштейном, дает убывание теплоемкости с температурой, причем теплоемкость стремится к нулю. Однако согласие теории с опытом получается только качественное. Так, по формуле Эйнштейна вблизи абсолютного нуля теплоемкость кристалла должна убывать с температурой по экспоненциальному закону, тогда как опыт приводит к более медленному убыванию по степенному закону. Можно было думать, что такое расхождение теории с опытом связано не с принципиальными недостатками теории, а обусловлено грубостью примененной модели. В теории Эйнштейна осцилляторы считаются независимыми. Но будет гораздо ближе к действительности, если их рассматривать связанными. В таком случае в теле возбуждается не колебание с одной частотой, а получится целый спектр частот
, а поэтому в вопросе о теплоемкости приводит к закону Дюлонга и Пти. При низких температурах формула, полученная Эйнштейном, дает убывание теплоемкости с температурой, причем теплоемкость стремится к нулю. Однако согласие теории с опытом получается только качественное. Так, по формуле Эйнштейна вблизи абсолютного нуля теплоемкость кристалла должна убывать с температурой по экспоненциальному закону, тогда как опыт приводит к более медленному убыванию по степенному закону. Можно было думать, что такое расхождение теории с опытом связано не с принципиальными недостатками теории, а обусловлено грубостью примененной модели. В теории Эйнштейна осцилляторы считаются независимыми. Но будет гораздо ближе к действительности, если их рассматривать связанными. В таком случае в теле возбуждается не колебание с одной частотой, а получится целый спектр частот 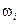 . Число этих частот равно 3N, т.е. числу степеней свободы N частиц, из которых состоит кристаллическое тело.
. Число этих частот равно 3N, т.е. числу степеней свободы N частиц, из которых состоит кристаллическое тело.
|
из
5.00
|
Обсуждение в статье: Пределы применимости классической теории твердого тела |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

