Основные правила комбинаторики

2015-11-07

600

Обсуждений (0)

0.00 из 5.00 0 оценок

12 3 4 5 Следующая ⇒

Условимся множество 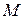, содержащее 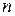элементов, называть, для краткости, 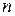-множеством. Напомним, что этот факт можно записать в виде .

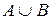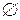1. Правило суммы. Рассмотрим следующую комбинаторную задачу: сколько элементов содержится в объединении m-множества и n-множества ? Ответ на этот вопрос очевиден в случае, когда множества и не пересекаются, т.е. . В этом случае множество 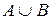содержит 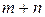элементов. Таким образом, справедливо следующее утверждение: если множества и конечны, причем , то

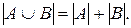(1)

В комбинаторике это очевидное утверждение называют правилом суммы иформулируют следующим образом:

Правило суммы.Если элемент а можно выбрать способами, а элемент b – m способами, причем любой способ выбора а отличается от любого способа выбора b, то выбор «а или b» можно сделать способами.

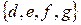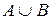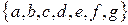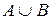Сложнее обстоит дело, если пересечение множеств и не пусто. Например, объединение множеств = и = состоит из семи элементов: = , а не из 6 + 4 = 10 элементов. Это объясняется тем, что элементы принадлежат обоим множествам и , а в объединение входят лишь один раз. Поэтому из суммы 6 + 4 приходится вычесть число 3, т.е. число элементов пересечения . Вообще для любых конечных множеств и имеет место равенство:

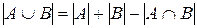. (2)

Таким образом, число элементов в объединении двух конечных множеств равно сумме чисел элементов в каждом из них, уменьшенной на число элементов в пересечении этих множеств.

Аналогично рассматривается вопрос о числе элементов в объединении нескольких конечных множеств . Если ограничимся только случаем, когда эти множества попарно не пересекаются (т.е. если при ), то с помощью математической индукции по числу к легко убедиться в справедливости равенства

(3)

Сложнее обстоит дело, если некоторые пары множества совокупности могут иметь непустые пересечения. Нам этот случай не понадобится и мы его опустим. Любопытный читатель может либо прочитать о нем в любой книге по комбинаторике, либо попытаться разобраться самостоятельно.

2. Правило произведения.Рассмотрим теперь следующую комбинаторную задачу: сколько элементов содержится в декартовом произведении m-множества A на n-множество В?

Ответ на этот вопрос дает следующее утверждение.

Т е о р е м а 1 (правило произведения). Если множество содержит элементов, а множество содержит n элементов, то их декартово произведение содержит элементов, т.е.

(4)

□ Пусть = и = 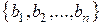.Выпишем элементы множества в виде прямоугольной таблицы:

, , …, ,

, , …, ,

…………………………………

, , …, .

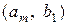В этой таблице m строк и n столбцов и поэтому число ее элементов равно 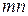, что и доказывает равенство (4).

В комбинаторике это утверждение называют правилом произведения иформулируют следующим образом:

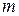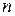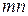Правило произведения.Если элемент можно выбрать способами, а элемент – способами, то упорядоченную пару можно выбрать способами.

Теорема 1 обобщается на любое конечное число множителей в декартовом произведении.

Т е о р е м а 2 (обобщенное правило произведения).Если конечные множества содержат соответственно элементов, то множество имеет элементов, т.е.

. (5)

□ Применим индукцию по числу .

База индукции.При равенство (5) справедливо.

Шаг индукции.Предположим истинность равенства (5) для , т.е. что

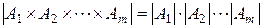, (6)

и рассмотрим . Легко видеть, что

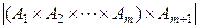= (7)

(это равенство вытекает из существования взаимно‑однозначного соответствия

между множествами и ). Используя теорему 1 и предположение индукции (6), отсюда получаем

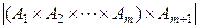= = . (8)

Из (7) и (8) следует теперь,

= .

Таким образом, мы доказали, что равенство (5) справедливо при .

Вывод.На основании обычного принципа математической индукции равенства (5) истинно при любом натуральном .