Соединения с повторениями

В § 1 уже рассмотрен вопрос о числе размещений с повторениями. Для полноты картины, рассмотрим еще перестановки и сочетания с повторениями.

1. Перестановки с повторениями.Перестановкой с повторениями порядка n и состава из элементов -множества называется упорядоченная n‑ка, в которой элементы встречаются соответственно раз, причем . Понятно, что две перестановки с повторениями одинакового порядка и состава могут отличаться друг от друга лишь порядком компонент. Например, и различные перестановки с повторениями порядка 7 и состава . Решим следующую комбинаторную задачу: найти число перестановок с повторениями порядка n, имеющих состав . Все такие перестановки можно получить следующим образом. Составим все перестановки без повторений из 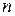различных элементов, включающих элементы . 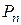Напомним, что их число равно 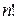. Если , то выберем произвольно элементов, не входящих в множество 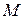, и отождествим их с во всех перестановках. Легко понять, что таким образом получим перестановки с повторениями порядка 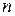и состава , где единица записана раз. Но различных среди них будет меньше во столько раз, сколько можно образовать перестановок без повторений из элементов, т.е. в раз. Таким образом, получим перестановок. Если 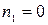, то переходим к . Если , то выберем произвольно элементов, не входящих во множество 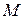, и отождествим их с во всех перестановках. Легко понять, что таким образом получим перестановок с повторениями порядка 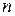и состава , где единица записана раз. Продолжая этот процесс, приходим к выводу о справедливости следующего утверждения:

Т е о р е м а 1.Число перестановок с повторениями порядка n, имеющих состав , вычисляется по формуле

= . (1)

Пример 1. Буквы слова «Математика» можно переставлять способами.

Из формулы (1) вытекает, что букв и букв можно переставлять способами. Но это число равно 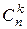. Значит, число перестановок с повторениями состава равно :

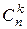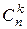= . (2)

Формула (2) позволяет записать формулу бинома Ньютона в следующем виде:

= + +…+ + … + ,

или в краткой форме

= ,

где суммирование распространено на все наборы такие, что .

С помощью индукции по числу слагаемых нетрудно убедится в справедливости следующего утверждения:

Т е о р е м а 2.Длялюбых натуральных чи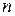сел , и любых действительных чисел справедлива формула

= , (3)

где суммирование распространено на все наборы такие, что .

Пример 2. = = .

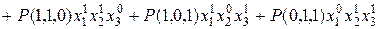2. Сочетания с повторениями.Найдем теперь число различных составов, которые могут иметь наборы длины 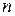, состоящие из элементов ‑множества 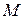. Каждый такой состав является упорядоченным набором, состоящим из чисел таких, что . Его можно записать в виде набора из нулей и единиц, заменив каждое число соответствующим числом единиц и поставив нуль после каждой группы единиц, кроме последней. Например, вместо набора можно написать , а вместо набора – набор . Число единиц, входящих в полученные наборы, равно , а число нулей равно . Поэтому число различных наборов такого вида равно числу перестановок с повторениями из n единиц и нулей, т.е.. . Но ввиду формулы (2) = .

Таким образом, мы доказали, что число составов наборов длины 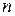, компоненты которых принадлежат данному k‑множеству, равно .

Различные составы наборов длины n из элементов k‑множества называют также сочетаниями с повторениями из элементов по 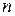. Их число обозначают .

Итак, справедлива

Т е о р е м а 3.Число всех сочетаниями с повторениями из элементов по 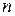вычисляется по формуле

= . (4)

Пример 3. Для множества 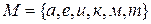всех букв, входящих в слово «Математика», число различных сочетаний с повторениями длины 10 равно = .

Вопросы для самоконтроля

1. Дать определение перестановки, сочетания и размещения без повторений. Вывести формулы для нахождения .

2. Сформулировать основные свойства чисел 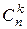и установить их связь с треугольником Паскаля и биномом Ньютона.

3. Решить задачи.

а) Сколько можно составить трехзначных чисел, если в каждом трехзначном числе любая цифра встречается только один раз?

б) Сколькими способами можно поставить на полке 10 различных книг, так чтобы выбранная книга стояла первой?

в) Сколькими способами можно сложить 6 различных книг в две сумки (порядок не имеет значения)?

4. Записать формулу исключений и включений для следующей задачи.

Часть жителей одного города умеют говорить только по-русски, часть только по-узбекски, а часть умеют говорить на обоих языках. По-узбекски говорят 85% жителей, по-русски – 75%. Сколько процентов жителей говорят на обоих языках?

5. Записать определение перестановок, сочетаний, и размещений с повторениями. Вывести соответствующие формулы.

6. Решить задачи:

а) Сколькими способами можно составить набор из 8 пирожных, если имеется 4 сорта?

б) Сколько нечетных трехзначных чисел можно составить из цифр 4, 5, 6?

в) Сколькими способами можно раскрасить трехполосный флаг, имея красный, белый и синий карандаши?

7. В чем суть принципа Дирихле? При решении каких комбинаторных задач он применяется?