 |
Главная |
Работа №14. Изучение скорости гидролиза уксусного ангидрида методом электрической проводимости
|
из
5.00
|
Гидролиз уксусного ангидрида протекает по уравнению
(СН3СО)2О + Н2О → 2СН3СООН
Реакция имеет второй порядок в ацетоне или в уксусной кислоте, однако в разбавленном водном растворе гидролиз идет как реакция первого порядка и практически до конца. Молярная концентрация воды здесь значительно больше молярной концентрации уксусного ангидрида, поэтому убыль воды за счет реакции мала и содержание ее в растворе можно считать постоянным, а скорость реакции – пропорциональной только концентрации уксусного ангидрида. Наиболее удобным способом изучения кинетики этой реакции является измерение электрической проводимости или сопротивления раствора, не требующее отбора проб для анализа. Электрическая проводимость системы со временем значительно возрастает вследствие образования уксусной кислоты.
Последовательность выполнения работы. Установить термостат на указанную температуру. В 100-миллилитровую мерную колбу поместить 12 мл уксусного ангидрида и довести объем раствора дистиллированной (предварительно термостатированной) водой до метки. В момент начала растворения уксусного ангидрида включить секундомер и не выключать его до конца опыта (до установления постоянного значения сопротивления раствора). Отметить по секундомеру время начала и конца растворения (при приливании воды четко видна граница раздела двух жидких слоев, после взбалтывания наблюдается помутнение; момент исчезновения мути принять за конец растворения). Среднее время принять за время начала реакции. Растворение проводить при энергичном перемешивании. Ячейку для измерения сопротивления, снабженную притертой крышкой, после двукратного ополаскивания исследуемым раствором заполнить этим же раствором. Электроды должны быть погружены в раствор на 0.5-1 см ниже уровня раствора.
В работе участвуют два исследователя. Один измеряет спротивление, другой следит за секундомером и записывает показания. Измерения проводятся тем чаще, чем выше температура опыта. 3-5 измерений следует провести через 30 секунд и затем через 1 мин до установления постоянного значения сопротивления. Результаты измерений записать в таблицу по образцу
Температура опыта………; концентрация раствора………
| № | Время от начала реакции, мин | Rt, Ом | 1/Rt | 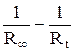
| 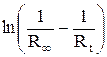
| k |
| . . |
При обработке результатов измерений следует учитывать, что исследуемая реакция является реакцией первого порядка. Пренебрегая неполной и меняющейся с концентрацией диссоциацией уксусной кислоты, можно принять в первом приближении, что увеличение электрической проводимости во времени пропорционально концентрации образующейся уксусной кислоты. Это грубое допущение, однако при расчете константы скорости происходит компенсация ошибок и конечный результат получается удовлетворительным. Количество образовавшейся уксусной кислоты пропорционально количеству взятого уксусного ангидрида, поэтому с упомянутым допущением общее увеличение электрической проводимости в течение реакции можно считать пропорциональным начальной концентрации уксусного ангидрида.
Если обозначить электрическую проводимость раствора в момент начала реакции χ0, в данный момент χt и соответствующую последнему измерению χ∞ (когда она уже не меняется), тогда с0=const(χ∞– χ0):
(с0 – сх) = const(χ∞– χ0) – const(χt– χ0) = const(χ∞– χt).
C учётом этого, кинетическое уравнение для реакции первого порядка примет вид:
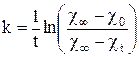 (6)
(6)
или, учтя далее, что  , где φ – константа прибора (см. с. 279 Практикума), получим
, где φ – константа прибора (см. с. 279 Практикума), получим
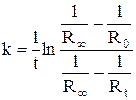 (7)
(7)
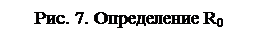 Сопротивление раствора в момент начала реакции R0 экспериментально не определяется, так как от начала реакции до первого измерения проходит некоторое время. Поэтому R0 определяют экстраполяцией, для чего строят график
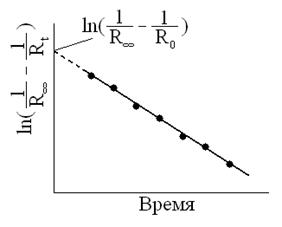
Сопротивление раствора в момент начала реакции R0 экспериментально не определяется, так как от начала реакции до первого измерения проходит некоторое время. Поэтому R0 определяют экстраполяцией, для чего строят график 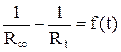 , откладывая время в минутах по оси абсцисс. Поскольку исследуемая реакция является реакцией первого порядка, экспериментальные данные в этих координатах должны укладываться на прямую. Экстраполируя полученную прямую до t = 0, находят
, откладывая время в минутах по оси абсцисс. Поскольку исследуемая реакция является реакцией первого порядка, экспериментальные данные в этих координатах должны укладываться на прямую. Экстраполируя полученную прямую до t = 0, находят 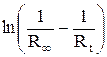 , а затем вычисляют R0 (рис. 7). Вычислив константу скорости реакции для каждого момента, определяют среднее ее значение и сравнивают с kср, рассчитанной по времени полупревращения (для реакции первого порядка) и полученной графически (тангенс угла наклона прямой к оси t). По константам скорости при двух температурах (вторую константу взять из справочника) рассчитать по следующим уравнениям энергию активации и значение предэкспоненциального множителя:
, а затем вычисляют R0 (рис. 7). Вычислив константу скорости реакции для каждого момента, определяют среднее ее значение и сравнивают с kср, рассчитанной по времени полупревращения (для реакции первого порядка) и полученной графически (тангенс угла наклона прямой к оси t). По константам скорости при двух температурах (вторую константу взять из справочника) рассчитать по следующим уравнениям энергию активации и значение предэкспоненциального множителя:
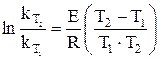 и
и 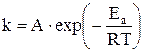 (8)
(8)
|
из
5.00
|
Обсуждение в статье: Работа №14. Изучение скорости гидролиза уксусного ангидрида методом электрической проводимости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

