Понятие множества. Способы задания. Виды множеств. Примеры

Модуль 1

Лекция 2. Элементы теории множеств

 

2.1.Понятие множества. Способы задания. Виды множеств. Примеры

2.2.Операции над множествами. Формула двойственности

2.3.Системы множеств

Программные положения

Теория множеств – один из фундаментальных разделов математики, его понятия являются основанием всех ее разделов. Мы будем рассматривать их в материалах модуля 2 «Введение в математический анализ» и модуля 3 «Введение в теорию вероятностей».

 

Методические рекомендации

Внимательно прочитайте текст лекции и посмотрите видео-фрагмент. Обратите внимание на определение действий над множествами, графическое их изображение.

Рекомендуемая литература

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 1, п. 1.1.-1.7

 

Дополнительно:

Я.Стюарт «Концепции современной математики» Главы1, 4

Контрольные вопросы

1. Что понимается под «множеством»

2. Приведите свои примеры различного задания множеств

3. Пусть А - множество положительных четных чисел, В – множество положительных нечетных чисел, С – множество целых положительных чисел, кратных 3. Ω – множество натуральных чисел . Опишите множества

A∩B, A\C, AUB, А∆В, A∩C,

4. Докажите вторую формулу Де Моргана

5. Укажите множество всех подмножеств множества А={*, #, @}. Сколько точек оно содержит?

6. Опишите закрашенную область с помощью знаков действий над множествами

 

 

 

Понятие множества. Способы задания. Виды множеств. Примеры

Под множеством понимают совокупность объектов, «собранных» вместе по какому-то принципу. Основным вопросом здесь является не природа этих объектов (называемых элементами или точками), а их принадлежность или непринадлежность данному множеству. Порядок следования элементов также не важен.

Если а есть один из объектов множества А, мы говорим, что а есть элемент А, или а принадлежит А, а если не принадлежит – то a – не является элементом множества А.

 

Замечание 2.1(1). То, что объекты, образующие множество, называются точками ничего не говорит об их истинной природе. Точками будут как точки числового множества расположенные на числовой прямой между, скажем, числами 2 и 4, так и неповторимые яркие индивидуальности, составляющие множество студентов 1 курса ВЕИП отделения дистанционного обучения.

 

Обозначения: Множества обозначают, как правило, заглавными латинскими буквами, элементы (точки) множества – строчными латинскими буквами. означает, что элемент (точка) x принадлежит множеству X, 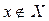, соответственно, не принадлежит (иногда непринадлежность обозначают чертой над знаком принадлежности ).

 

 

Если мы хотим описать множество, мы делаем это, открыв фигурные скобки. Например, X={множество студентов 1 курса ВЕИП отделение дистанционного обучения}.

Способы задания множества:

 

1) Простым перечислением элементов

A={красный, желтый, зеленый}, описывающее цвета огней светофора

Очевидно, что перечисление элементов удобно

только в том случае, когда множество элементов мало или произвольный элемент характеризуется свойством, которое легко описать.

 

2)Заданием вида элемента

Часто при перечислении множества используется

описание характеристического свойства элементов этого множества. Например, С = {1³,2³,3³,..., n³,...} описывает множество кубов всех натуральных чисел, а S = {1²,2²,3²,... ,n²} описывает множество квадратов всех положительных чисел, которые меньше или равны n.

 

 

3) Заданием некоего общего характеристического свойства элементов множества R={множество действительных чисел} (более подробно об определении множества действительных чисел см п.4.1)

Другой пример: А = {x| x – четное число}. Знак | (или : заменяет обороты «такой что», «такие что», «обладающий свойствами»)

 

В общем случае множество задается именно путем указания характеристического свойства, т.е. свойства, которому удовлетворяют элементы данного множества, и только они. Для задания обычно используются фигурные скобки, а внутри них приводится характеристическое свойство, описывающее множество. Таким образом, множество {х : х обладает свойством Р} предполагается содержащим только те объекты, которые имеют свойство Р. Например, {х : х — футболист, играющий за РФ} — множество, состоящее из всех футбольных игроков, защищающих честь России на разнообразных турнирах. Запись {х : х —- гражданин России} описывает множество всех граждан России. Способ задания множества должен быть адекватным, т.е. должен полностью определять множество. Это не представляет труда, если объекты множества перечислены. Рассмотрим, однако, множество А = {х : х — высокий студент данного курса} или В = {х : х — хороший студент данного курса}. Если различным студентам курса предложить определить множества A и В, они могут сделать это неоднозначно, выбирая в качестве элементов как множества А, так и множества В не одних и тех же людей. При рассмотрении множества С = {х : х — привлекательная (или красивая) студентка группы} выбрать элементы множества С не только трудно, но не стоит даже пытаться это сделать. Однако, если множество А = {х : х — студент данной группы, рост которого выше 180см} и В = {х : х — студент данной группы, средний балл которого не ниже 4}, то можно сказать определенно, является ли данный студент элементом А или В, так что А и В действительно есть множества.

 

Множество может вообще не содержать никаких элементов. Тогда оно называется пустым множеством и обозначается Ø. Например, множество клетчатых крокодилов пусто, поскольку вы не найдете ни одного крокодила, который был бы клетчатым.

Множество может состоять только из одного элемента. Такое множество называется одноточечным (одноэлементным). X = {x}. Например, множество президентов Российской Федерации представлено ровно одним человеком.

Множество может содержать конечное число элементов, например, множество студентов вашего курса. Такое множество называется конечным.

Кроме того, множество может содержать бесконечное число элементов – бесконечное множество. В свою очередь бесконечное множество может быть счетным, то есть его элементы можно занумеровать в (бесконечную) последовательность. Примером может служить, скажем, множество натуральных чисел (каждое число задает и свой номер). А также оно может быть несчетным, таково, например, множество действительных чисел (о числе элементов множества подробнее см. тему 6.2.)

 

Замечание 2.1(2)

Множество нельзя задавать совсем уж произвольно. Рассмотрим известный исторический пример – «парадокс брадобрея». В некотором городе брадобрей бреет всех тех, кто не бреется сам. Принадлежит ли сам брадобрей множеству тех, кого он бреет?

Есть два основных направления «борьбы» с такого рода ситуациями:

- «наивная теория множеств» Г.Кантора, в которой запрещаются все действия и операции, ведущие к парадоксам.

- аксиоматический, при котором множество есть нечто, удовлетворяющее набору аксиом (системы Цермело-Френкеля, Гёделя-Бернайса)

 

Определение 2.1. (1)

Если все элементы множества A содержатся и в множестве B (но не наоборот), говорят, что множество A является собственным подмножеством множества B, что обозначается как A 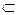B. Если же, помимо этого, не исключается и совпадение А и В, используется обозначение A B.

Так, например, множество городов Северо-западного региона России является собственным подмножеством множества российских городов, а множество целых положительных чисел, являясь подмножеством множества натуральных чисел, совпадает с ним.

 

Всякое множество имеет по крайней мере 2 подмножества – пустое множество и себя самое.

= B

= A

Определение 2.2.(3)

Множества равны, если они содержат одни и те же элементы, порядок элементов, как уже отмечалось, роли не играет.

Иначе говоря,

A=B , если для любого x выполняется: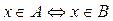

 

Например, если А ={2,4,6}, а В = {х : х есть четное положительное целое число, которое меньше 7}, тогда А и В — равные множества.

Как уже упоминалось, если не оговаривается обратное, порядок следования элементов в множестве не имеет значения, как и наличие повтора элементов (то есть множество однозначно определяется только элементами, которые оно содержит) , поэтому A={1,2,3,4,5}, B={2,3,1,4,5}, C={1,1,2,3,3,3,5,4,4,4,4}, A = B = C.

 

 

Можно определить равенство множеств и следующим образом:

A=B

Если A B и 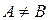то говорят, что A - собственное подмножество множества B.

 

Таким образом, доказательство равенства множеств А и В состоит из двух

этапов:

1) Доказать, что А есть подмножество В.

2) Доказать, что В есть подмножество А.

 

Замечание 2.2.(2). Рассматривая множества и действия над ними, обычно имеют в виду существование некоторого основного (базового, универсального) множества, из которого черпают примеры множеств. Мы будем обозначать его Ω (это обозначение принято в теории вероятностей, к изучению которой мы перейдем во втором семестре). В теории множеств его обозначают какой-либо заглавной латинской буквой, например М или U.

В некотором смысле основное множество Ω и пустое множество Ø представляют собой противоположности, поскольку пустое множество не содержит элементов, а универсальное множество содержит "все" элементы.

 

 

2.2.Операции над множествами. Формула двойственности

Рис.2.2.(1)

Множества удобно изображать в виде рисунка, который называется кругами Эйлера (в теории множеств) или диаграммами Венна(Вьенна) (в логике). На рисунке 2.2.(1) основное множество (пространство)W изображено в виде прямоугольника, а произвольное множество A, заключено в эллипс. Сами элементы (точки) на кругах Эйлера не изображаются, а информация о соотношении между их множествами содержится в расположении границ соответствующих областей.

Суммой (объединением)двух множествАиB(обозначается AUB или А+В) называется множество, состоящее из всех элементов, принадлежащих по крайней мере одному из множеств А или B, возможно и обоим, но по крайней мере одному – точно.

 

Рис.2.2.(2)

Приведем пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B - в том, что в мишень попадает 2-й. Событие AUB означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.

Рис.2.2.(3)

Произведением (пересечением) A∩B (или АВ, А×В )множеств А и B называется событие, состоящее из всех тех элементарных исходов, которые принадлежат и А и B.

 

 

Если у множеств нет общих точек (см рис.2.2.(4)), их

Рис. 2.2.(4) их пресечение пусто A∩ B = Ø

 

 

Разностью А\B или А-B событий А и B называется событие, состоящее из всех исходов события А, не благоприятствующих событию B. Диаграмма Венна разности событий А и Bизображена на рисунке 2.2.(5).

Рис.2.2.(5)

В условиях рассмотренного выше примера событиеА\B заключается в том, что первый стрелок попал в мишень, а второй промахнулся.

 

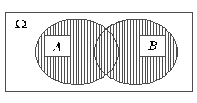
Симметрической разностью А∆В называется событие, состоящее из всех исходов, входящих в события А и В по-отдельности, но не принадлежащие им обоим (на рис. 2.2.(3)) – незаштрихованная область внутри А и В). А∆В = AUB \ A∩B

 

Множество = W \ A = С_ΩА, состоящее из всех точек , не принадлежащих множеству А (но принадлежащих определенному основному множеству Ω) дополнением множестваА (до множества (пространства) Ω). (заштрихованная область вне множества А на рис. 2.2.(6)).

 

 

Рис. 2.2.(6)

 

 

Замечание. Существенно, что мы находимся все время в рамках одного и того же основного множества – Ω, поскольку без него операцию дополнения просто не определить.

 

Пример 2.2.(1)

А={1,2,3,4,5,6}

B={0,2,4,6,8,10}

C={9,10}

Ω={0,1,2,3,4,5,6,7,8,9,10}

 

AUB = {0,1,2,3,4,5,6,8,10}

A∩B = {2,4,6}

A∩C = Ø

А\ B = {1,3,5}

А∆В = {0,1,3,5,8,10}

= {0,7,8,9,10}

 

Примеры 2.2.(2)

 

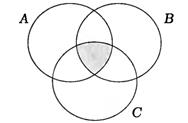закрашенная область – множество A ∩B ∩C

 

 

закрашенная область – множество (AUB)\ C

 

 

Непосредственно из введенных определений следуют равенства: AU =W; A∩ =Æ; ∩ ; = . Два последних равенства называются формулами Де Моргана.

 

Теорема 2.2. Первая формула Де Моргана (Первая формула двойственности)

 

∩

Доказательство

Аналогичное доказательство второй формулы Де Моргана оставим в качестве упражнения.

 

Системы множеств

 

Определение 2.3 (1).

Системой множеств называется такое множество, точки которого сами являются множествами, то есть, своего рода множество множеств. Как правило рассматриваются системы таких множеств, каждое из которых является подмножеством основного множества Ω. Системы множеств обычно обозначаются готическими («кучерявыми») буквами.

 

Для нужд теории вероятностей нам понадобится в первую очередь понятие сигма-алгебры множеств.

 

Определение 2.3. (2)

Система подмножеств множества Ω называется σ-алгеброй А, если выполнены следующие условия:

 

1) Ω ϵ А

2) Если множества А_i ϵ А, i = 1, 2, 3, …, то Σ^∞_i=1 A_i ϵ A

3) Если множество А ϵ А, то и Ā ϵ А

 

Простейшим примером σ-алгебры является множество всех подмножеств Ω.

 

Замечание. Совокупность множеств называется (просто) алгеброй, если для этих множеств выполняются условия 1) и 3), а условие 2) формулируется следующим образом: Если А₁ ϵ А и А₂ ϵ А, то А₁ + А₂ ϵ А. Нетрудно видеть, что данное условие слабее, так как оно следует из условия для σ-алгебры.