 |
Главная |
Неявное задание кривой
|
из
5.00
|
Рассмотрим геометрическое место точек M(х, у), координаты которых удовлетворяют уравнению:
 , ,
| (7) |
где функция F(x,у) непрерывно дифференцируема по обоим аргументам в области U на плоскости xy.
Для того чтобы можно было утверждать, что это геометрическое место точек в окрестности некоторой точки М0 области U образует линию (простую дугу), надо задать начальную точку М0(х0, у0), координаты которой удовлетворяют уравнению (1) и не обращают в нуль одновременно обе частные производные:
 . .
| (8) |
Теорема 1. Пусть уравнение (7) 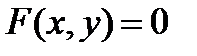 допускает начальную точку
допускает начальную точку  ; функция
; функция  непрерывно дифференцируема по каждому аргументу в окрестности начальной точки
непрерывно дифференцируема по каждому аргументу в окрестности начальной точки  , и производная
, и производная  в этой точке отлична от нуля:
в этой точке отлична от нуля:
 .
.
Тогда существует одна и только одна функция  , которая в некоторой окрестности начальной точки удовлетворяет уравнению (7) и при
, которая в некоторой окрестности начальной точки удовлетворяет уравнению (7) и при  принимает значение
принимает значение  . Эта функция имеет в данной окрестности непрерывную производную
. Эта функция имеет в данной окрестности непрерывную производную
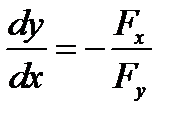 .
.
Доказательство данной теоремы следует из теорем о существовании неявной функции и её дифференцируемости.[12 пп.206, 207]
Итак, угловой коэффициент касательной равен  , но тогда уравнение касательной в точке
, но тогда уравнение касательной в точке  принимает вид:
принимает вид:
 , ,
| (9) |
а уравнение нормали имеет вид:
 . .
| (10) |
Следствие. Уравнение
 ,
,
где F(x,y)- функция, допускающая в области U плоскости непрерывные частные производные по обоим аргументам, не обращающиеся одновременно в нуль, определяет в этой области регулярный кусок кривой, если найдется в ней хотя бы одна точка М0(х0,у0), координаты которой, удовлетворяют уравнению.
Особые точки
Мы предполагаем, что функция F(х,у) непрерывно дифференцируема три раза по обоим аргументам.
Условие регулярности кривой (7) нарушается в точках, где обе частные производные первого порядка равны нулю:
 . .
| (11) |
Следовательно, подлежат исследованию точки, координаты которых удовлетворяют трем уравнениям: (7), (11). Если в такой точке не все производные 2-го порядка равны нулю, то точка называется двойной.
1. Касательные в двойной точке.
Через двойную точку М0 может проходить не более двух ветвей кривой с угловыми коэффициентами касательных  , определяемыми уравнением
, определяемыми уравнением
 , ,
| (12) |
где 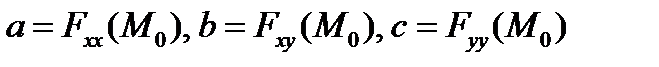 .
.
2. Изолированная точка.
Введем обозначение
 .
.
Если  , то в достаточно малом круге с центром M0, кроме этой точки, нет других, координаты которых удовлетворяли бы уравнению(7).
, то в достаточно малом круге с центром M0, кроме этой точки, нет других, координаты которых удовлетворяли бы уравнению(7).
Особая точка называется изолированной.
3. Точка самопересечения.
Если  < 0, то через точку M0 проходят две простые дуги с различными касательными (уравнение (12) имеет два различных корня к1 и к2).
< 0, то через точку M0 проходят две простые дуги с различными касательными (уравнение (12) имеет два различных корня к1 и к2).
Особая точка называется точкой самопересечения(узел).
4. Точки возврата и самоприкосновения.
Если в точке  кривой (7)
кривой (7)  =0, то для исследования поведения кривой вблизи данной точки требуются более сложные рассуждения с привлечением производных 3-го (а порой и более высокого) порядка. Рассмотрим основные возможности, которые здесь представляются.
=0, то для исследования поведения кривой вблизи данной точки требуются более сложные рассуждения с привлечением производных 3-го (а порой и более высокого) порядка. Рассмотрим основные возможности, которые здесь представляются.
1) Вблизи точки  , кроме неё самой, нет точек кривой, т.е.
, кроме неё самой, нет точек кривой, т.е.  - изолированная точка (как и в п.2).
- изолированная точка (как и в п.2).
2) Через точку  проходят две ветви кривой, имеющие в ней общую касательную.
проходят две ветви кривой, имеющие в ней общую касательную.
a) Точка  - точка самоприкосновения (рис. 3)
- точка самоприкосновения (рис. 3)
b) Точка  - точка возврата первого рода (рис. 4)
- точка возврата первого рода (рис. 4)
c) Точка  - точка возврата второго рода (рис. 5)
- точка возврата второго рода (рис. 5)

| 
| 
|
| Рисунок 3 | Рисунок 4 | Рисунок 5 |
Асимптоты
Для отыскания асимптот, параллельных оси абсцисс, надо искать предельное значение ординаты y=b при  . Если кривая — алгебраическая (F(x,у) — многочлен), то достаточно приравнять к нулю коэффициент при старшей степени х. Если полученное уравнение допускает решение y=bi, то оно даст все асимптоты:
. Если кривая — алгебраическая (F(x,у) — многочлен), то достаточно приравнять к нулю коэффициент при старшей степени х. Если полученное уравнение допускает решение y=bi, то оно даст все асимптоты:
 .
.
Действительно, если собрать члены с одинаковыми степенями х и записать уравнение кривой в виде
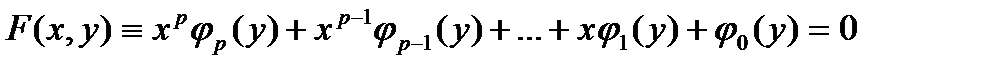 ,
,
то, деля любые части уравнения на xp:

и переходя к пределу при  ,
,  , заметим, что все функции
, заметим, что все функции  обратятся в
обратятся в  и сохранят конечные значения, следовательно, все члены уравнения, имеющие делителем х, обратятся в нуль, и для определения b мы получим уравнение
и сохранят конечные значения, следовательно, все члены уравнения, имеющие делителем х, обратятся в нуль, и для определения b мы получим уравнение
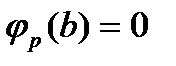 .
.
Аналогично находятся асимптоты, параллельные оси ординат.
Чтобы найти асимптоты, не параллельные осям координат  ,
,
надо найти пределы  .
.
Полагая  , подставляя в уравнение
, подставляя в уравнение  и исключая ординату, мы получаем уравнение:
и исключая ординату, мы получаем уравнение:

надо найти
 .
.
Аналогично, полагая
 ,
,
исключаем из уравнения F(x,у)=0 ординату у. Поскольку k известно, получаем уравнение:

и снова имеем:
 .
.
|
из
5.00
|
Обсуждение в статье: Неявное задание кривой |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

