 |
Главная |
Множества и отображения
|
из
5.00
|
1.1 Множества и действия над ними. Ту или иную совокупность (класс, семейство) рассматриваемых объектов будем называть множеством, а соответствующие объекты – элементами или точками этого множества.
Далее запись
 означает, что элемент
означает, что элемент  принадлежит множеству принадлежит множеству  , а запись , а запись
   ,
- что он не принадлежит этому множеству.
Множество состоящее из конечного числа элементов называется конечным, в противном случае оно называется бесконечным.
Для описания конечных множеств достаточно перечислить все их элементы, при этом они обычно заключаются в фигурные скобки. В частности, запись ,
- что он не принадлежит этому множеству.
Множество состоящее из конечного числа элементов называется конечным, в противном случае оно называется бесконечным.
Для описания конечных множеств достаточно перечислить все их элементы, при этом они обычно заключаются в фигурные скобки. В частности, запись
 означает, что множество А состоит из всех элементов от «а» до «я», а запись
означает, что множество А состоит из всех элементов от «а» до «я», а запись 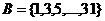 , что множество , что множество  состоит из всех нечетных чисел от 1 до 31.
Аналогично могут описываться и некоторые бесконечные множества. Например, состоит из всех нечетных чисел от 1 до 31.
Аналогично могут описываться и некоторые бесконечные множества. Например,
 - множество всех натуральных чисел, а
- множество всех натуральных чисел, а
 -множество всех целых чисел. Множество, состоящее из одного элемента
-множество всех целых чисел. Множество, состоящее из одного элемента  , обозначается , обозначается  .
Часто множества образуются на основании какого-то общего свойства своих элементов. В этом случае удобно другое их описание. А именно, пусть .
Часто множества образуются на основании какого-то общего свойства своих элементов. В этом случае удобно другое их описание. А именно, пусть  - некоторое свойство и запись - некоторое свойство и запись  означает, что элемент означает, что элемент  обладает свойством обладает свойством  . Тогда запись . Тогда запись
 означает, что множество
означает, что множество  состоит из всех объектов, обладающих свойством состоит из всех объектов, обладающих свойством  , а запись , а запись
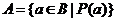 ,
что множество ,
что множество  состоит из всех тех элементов множества состоит из всех тех элементов множества  , которые обладают свойством , которые обладают свойством  . Например, . Например,
 - множество всех рациональных чисел, т.е. множество всех обыкновенных дробей.
Далее если, как обычно, через
- множество всех рациональных чисел, т.е. множество всех обыкновенных дробей.
Далее если, как обычно, через  обозначить множество всех вещественных чисел, т.е. множество всех рациональных и всех иррациональных чисел, то, например, запись обозначить множество всех вещественных чисел, т.е. множество всех рациональных и всех иррациональных чисел, то, например, запись
 означает, что
означает, что  – множество всех вещественных корней уравнения – множество всех вещественных корней уравнения  (очевидно, что (очевидно, что  ).
К числу множеств удобно отнести и, так называемое, пустое множество, которое по определению не содержит ни одного элемента. Пустое множество обозначается одним из символов L или Ø.
Определение 1. Если каждый элемент множества ).
К числу множеств удобно отнести и, так называемое, пустое множество, которое по определению не содержит ни одного элемента. Пустое множество обозначается одним из символов L или Ø.
Определение 1. Если каждый элемент множества  является также и элементом множества является также и элементом множества  , то множество , то множество  называется подмножеством множества называется подмножеством множества  , при этом пишут , при этом пишут 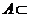  или или    .
Если множество .
Если множество  не является подмножеством множества не является подмножеством множества  , то пишут , то пишут  .
Очевидно, .
Очевидно,  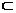  для любого множества для любого множества  . По определению полагаем также, что Ø . По определению полагаем также, что Ø 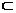  .
Определение 2. Множества .
Определение 2. Множества  и и  называют равными друг другу и пишут называют равными друг другу и пишут  , если они состоят из одних и тех же элементов или, иначе, если , если они состоят из одних и тех же элементов или, иначе, если  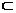  и и  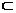  .
Далее иногда будет использоваться специальная символика:
ך – знак логического отрицания (читается “не”);
∧ – знак конъюнкции или логического умножения (читается “и”);
∨ – знак дизъюнкции или логического сложения (читается “или”);
⇒ – знак импликации или логического следования (читается “влечет”);
⇔ – знак эквивалентности (читается “эквивалентно”, “равносильно”,
а также “необходимо и достаточно”, “тогда и только тогда”, “если
и только если” и т.п.)
∃ – квантор существования (читается “существует”, “найдется”);
∀ – квантор всеобщности ( читается “любой” или “для любого”);
≜ – равно по определению.
С помощью этой символики, например, определениям 1 и 2 можно придать следующую краткую форму: .
Далее иногда будет использоваться специальная символика:
ך – знак логического отрицания (читается “не”);
∧ – знак конъюнкции или логического умножения (читается “и”);
∨ – знак дизъюнкции или логического сложения (читается “или”);
⇒ – знак импликации или логического следования (читается “влечет”);
⇔ – знак эквивалентности (читается “эквивалентно”, “равносильно”,
а также “необходимо и достаточно”, “тогда и только тогда”, “если
и только если” и т.п.)
∃ – квантор существования (читается “существует”, “найдется”);
∀ – квантор всеобщности ( читается “любой” или “для любого”);
≜ – равно по определению.
С помощью этой символики, например, определениям 1 и 2 можно придать следующую краткую форму:
 , ,
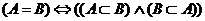 .
Определение 3.Объединениеммножеств .
Определение 3.Объединениеммножеств  и и  называется множество называется множество
 .
Определение 4. Пересечением множеств .
Определение 4. Пересечением множеств  и и  называется множество называется множество
 .
По аналогии с определениями объединения и пересечения двух множеств вводится определение объединения и пересечения любого числа множеств (как конечного так и бесконечного).
Очевидно, имеют место следующие свойства операций ∪ и ∩:
а) .
По аналогии с определениями объединения и пересечения двух множеств вводится определение объединения и пересечения любого числа множеств (как конечного так и бесконечного).
Очевидно, имеют место следующие свойства операций ∪ и ∩:
а)  (коммутативность операции ∪);
б) (коммутативность операции ∪);
б)  (коммутативность операции ∩);
в) (коммутативность операции ∩);
в)  (ассоциативность операции ∪);
г) (ассоциативность операции ∪);
г)  (ассоциативность операции ∩);
д) (ассоциативность операции ∩);
д)  и
и
 (дистрибутивные свойства операций ∪ и ∩);
Определение 5. Разностью между множеством
(дистрибутивные свойства операций ∪ и ∩);
Определение 5. Разностью между множеством  и множеством и множеством  называется множество называется множество
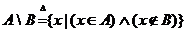 .
Определение 6. Прямым(или декартовым) произведениеммножеств .
Определение 6. Прямым(или декартовым) произведениеммножеств  и и  называется множество всех упорядоченных пар называется множество всех упорядоченных пар  таких, что таких, что  .
Прямое произведение множеств .
Прямое произведение множеств  и и  обозначается обозначается  . Отметим, что вообще говоря, . Отметим, что вообще говоря,   .
Примеры.
i) Прямое произведением двух отрезков .
Примеры.
i) Прямое произведением двух отрезков  и и  можно рассматривать как прямоугольник на плоскости,
ii) Прямое произведение круга и отрезка можно рассматривать как цилиндр в пространстве,
iii) Прямое произведение можно рассматривать как прямоугольник на плоскости,
ii) Прямое произведение круга и отрезка можно рассматривать как цилиндр в пространстве,
iii) Прямое произведение  множества вещественных чисел множества вещественных чисел  на себя
можно рассматривать как плоскость с введенной в ней декартовой системой координат
1.2.Понятие отображения.
Пусть на себя
можно рассматривать как плоскость с введенной в ней декартовой системой координат
1.2.Понятие отображения.
Пусть  и и  – произвольные множества. Правило – произвольные множества. Правило 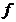 , по которому каждому элементу , по которому каждому элементу 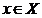 ставится в соответствие определенный, и при том единственный, элемент ставится в соответствие определенный, и при том единственный, элемент  называется отображением множества называется отображением множества  во множество во множество  , при этом множество , при этом множество  называется областью определения отображения называется областью определения отображения 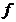 , а множество , а множество  –областью значений этого отображения.
Отображение –областью значений этого отображения.
Отображение 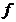 множества множества  во множество во множество  обозначают одним из следующих способов: обозначают одним из следующих способов:
 ;
или ;
или
 , ,  , ,  ;
Кратко его обозначают также ;
Кратко его обозначают также
 ,
или ,
или
 ,
если ранее уже были описаны его область определения и область значения.
Если элемент ,
если ранее уже были описаны его область определения и область значения.
Если элемент 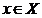 отображением отображением  сопоставляется элементу сопоставляется элементу  , то элемент , то элемент 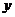 называют образом элемента называют образом элемента  при отображении при отображении 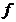 или значением отображения или значением отображения 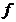 в точке в точке  и обозначают и обозначают  , при этом пишут , при этом пишут  , а сам элемент , а сам элемент  , который отображением , который отображением 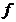 сопоставляется элементу сопоставляется элементу  называют прообразом элемента y при отображении называют прообразом элемента y при отображении 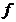 .
Подчеркнем, что образ .
Подчеркнем, что образ  элемента элемента 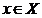 при отображении при отображении  (по определению отображения) определяется однозначно, а прообразов элемента (по определению отображения) определяется однозначно, а прообразов элемента  при том же отображении может быть несколько. Множество всех прообразов элемента при том же отображении может быть несколько. Множество всех прообразов элемента  при отображении при отображении  обозначается обозначается  .
Элемент .
Элемент  из области определения отображения из области определения отображения 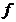 часто называют независимой переменной или аргументомэтого отображения, а элемент часто называют независимой переменной или аргументомэтого отображения, а элемент  из области значений, соответственно, называют зависимой переменной.
-----------------------------------------------------------------------------------
Множество из области значений, соответственно, называют зависимой переменной.
-----------------------------------------------------------------------------------
Множество
 называется графиком отображения
называется графиком отображения  .
-----------------------------------------------------------------------------------------------
Пусть задано отображение .
-----------------------------------------------------------------------------------------------
Пусть задано отображение  и множество и множество  .Определим новое отображение .Определим новое отображение 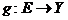 ,полагая, что ,полагая, что 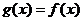  . Так определенное отображение . Так определенное отображение  называется сужением отображения называется сужением отображения  на множество на множество  и обычно обозначается и обычно обозначается  .
--------------------------------------------------------------------------------------
Образом множества .
--------------------------------------------------------------------------------------
Образом множества  при отображении при отображении  называют множество называют множество
 .
-------------------------------------------------------------------------------------
Образ .
-------------------------------------------------------------------------------------
Образ 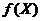 области определения отображения области определения отображения  называют множеством значений этого отображения.
Ясно, что называют множеством значений этого отображения.
Ясно, что   , но при этом не исключено, что , но при этом не исключено, что   , т.е. понятия множества значений и области значений отображения , т.е. понятия множества значений и области значений отображения  , вообще говоря, разные понятия.
Отображения , вообще говоря, разные понятия.
Отображения  и и  называют равными друг другу и пишут называют равными друг другу и пишут 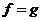 , если , если  и и  .
------------------------------------------------------------------------------------
Отображение .
------------------------------------------------------------------------------------
Отображение
 будем называть
а) функцией, если
будем называть
а) функцией, если  (в частности, отображение (в частности, отображение  , где , где  – произвольное, необязательно числовое множество, является функцией)
б) числовой функцией или функцией одной переменной, если – произвольное, необязательно числовое множество, является функцией)
б) числовой функцией или функцией одной переменной, если  и и  .
------------------------------------------------------------------------------------
Отображение .
------------------------------------------------------------------------------------
Отображение  множества натуральных чисел множества натуральных чисел  в произвольное множество в произвольное множество  будем называть последовательностью (во множестве будем называть последовательностью (во множестве ), при этом, если ), при этом, если 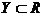 , то ее будем называть числовой последовательностью или, также, последовательностью вещественных чисел.
Последовательность , то ее будем называть числовой последовательностью или, также, последовательностью вещественных чисел.
Последовательность  обозначается символом обозначается символом  , а иногда и просто , а иногда и просто  , где , где  ≜ ≜  –образ точки –образ точки  при отображении при отображении  .
1.3. Суперпозиция отображений.
Пусть даны отображения .
1.3. Суперпозиция отображений.
Пусть даны отображения
 и и  .
Новое отображение .
Новое отображение
 ,
определенное по следующему правилу: ,
определенное по следующему правилу:
 называют суперпозициейотображений
называют суперпозициейотображений  и и  .
Суперпозицию .
Суперпозицию  отображений отображений 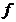 и и  обычно обозначают символом обычно обозначают символом  (таким образом, (таким образом,  ), при этом если оба отображения ), при этом если оба отображения 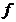 и и  являются функциями, то их суперпозицию являются функциями, то их суперпозицию  называют сложной функцией.
Пусть теперь даны три отображения называют сложной функцией.
Пусть теперь даны три отображения
 , ,  и и 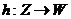 Тогда можно определить следующие два новых отображения:
Тогда можно определить следующие два новых отображения:
 и и 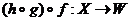 Утверждение 1.
Утверждение 1.  .
Доказательство. Очевидно, для любого .
Доказательство. Очевидно, для любого 
 ■
Таким образом, вместо ■
Таким образом, вместо  и и 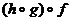 можно писать можно писать  .
1.4. Обратное отображение.
Определение 1. Отображение .
1.4. Обратное отображение.
Определение 1. Отображение  называется
а) сюръективнымили отображением “на”, если называется
а) сюръективнымили отображением “на”, если  ;
b) инъективнымили взаимно однозначным отображением «в», если ;
b) инъективнымили взаимно однозначным отображением «в», если
 из того, что из того, что 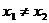 следует, что следует, что  (или, равносильно, если (или, равносильно, если
 из того, что из того, что  следует, что следует, что  );
в) биективнымили взаимно однозначным отображением «на» или также взаимно однозначным соответствием, если оно одновременно инъективно и сюръективно.
-------------------------------------------------------------------------------------------------
Пусть отображение );
в) биективнымили взаимно однозначным отображением «на» или также взаимно однозначным соответствием, если оно одновременно инъективно и сюръективно.
-------------------------------------------------------------------------------------------------
Пусть отображение  устанавливает взаимно однозначное соответствие между множествами устанавливает взаимно однозначное соответствие между множествами  и и  , т.е. является биективным. Тогда можно определить новое отображение , т.е. является биективным. Тогда можно определить новое отображение  , полагая, что , полагая, что  его образом его образом  при отображении при отображении  является тот единственный элемент является тот единственный элемент  , образом которого при отображении , образом которого при отображении  является соответствующий элемент является соответствующий элемент 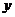 : :
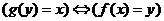 Так определенное отображение g называется обратнымк отображению
Так определенное отображение g называется обратнымк отображению 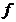 и обозначается и обозначается  , т.е. , т.е.  .
Отображение .
Отображение  такое, что такое, что
 , ,  ,
называется тождественным отображением множества ,
называется тождественным отображением множества  в себя.
Непосредственно из определения обратного отображения следует, что
а) обратное отображение биективно;
б) имеют место равенства в себя.
Непосредственно из определения обратного отображения следует, что
а) обратное отображение биективно;
б) имеют место равенства
 , т.е. , т.е.  (2.1)
и (2.1)
и
 , т.е. , т.е.  ; (2.2)
в) обратным к отображению ; (2.2)
в) обратным к отображению  является отображение является отображение  , т.е. , т.е.
 и, следовательно, отображения
и, следовательно, отображения 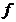 и и  являются взаимно обратными.
Если отображение являются взаимно обратными.
Если отображение  является числовой функцией и имеет обратное отображение является числовой функцией и имеет обратное отображение  , то это обратное отображение называется обратной функцией (к функции , то это обратное отображение называется обратной функцией (к функции  ). ).
| Примечания |
|
из
5.00
|
Обсуждение в статье: Множества и отображения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |
Популярное:
Почему двоичная система счисления так распространена?: Каждая цифра должна быть как-то представлена на физическом носителе...
Почему люди поддаются рекламе?: Только не надо искать ответы в качестве или количестве рекламы...
Почему стероиды повышают давление?: Основных причин три...
Личность ребенка как объект и субъект в образовательной технологии: В настоящее время в России идет становление новой системы образования, ориентированного на вхождение...

©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (547)
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

