 |
Главная |
Основные методы решения задач, содержащих параметр
|
из
5.00
|
КУРСОВАЯ РАБОТА
по курсу «Элементарная математика»
тема: «Задачи с параметром в материалах ГИА и методы их решения
(по материалам ЕГЭ за последние 5 лет)»
Выполнил студент:
11 группы 1 курса
очной формы обучения
физико-математического
факультета
Агабабова Анастасия Константиновна
Научный руководитель:
ст. преподавательВысоцкая Полина Андреевна
Дата защиты: «___» __________ 2018 г.
Оценка:___________________________
__________________________________
(подпись научного руководителя)
Регистрационный номер _________
Дата регистрации:_______________
Москва
Содержание
Введение…………………………………………………………………………3
1. Классификация задач с параметрами………………………………………….4
2. Основные методы решения задач, содержащих параметр………….....……13
2.1. Аналитический метод…………………………………………………..….13
2.2. Графический метод…………………………………………………..……. 17
Заключение……………………………………………………………………...27
Литература………………………………………………………………………28
Введение
Задачи с параметром составляют важную часть современного математического образования. Они помогают в формировании логического мышления, отработки навыка анализа и системного подхода к решению.
Задания с параметром были введены в материалы ЕГЭ ещё с 2001 года, когда экзамен проводился в форме эксперимента. С 2009 года ЕГЭ является единственной формой выпускных экзаменов, где также содержатся задачи с параметром.Введение параметра способствовало появлению качественно новых типов задач,а также таких, как решение уравнений и неравенств.
Одной из причин введения задач данного типа в итоговую аттестацию является то, что задачи с параметром встречаются не только в математике, но и в других науках, например, многие закономерности в физике описываются уравнениями и неравенствами с параметром. Кроме этого задания помогают оценить сформированность логического мышления.
Цель работы: изучить методы решения задач с параметром из материалов ЕГЭ.
Задачи работы заключаются в получении общего представления о заданиях с параметрами в материалах ЕГЭ, классификации методов их решения,а такжев разработке набора упражнений, на примерах которых реализуются эти методы.
Классификация задач с параметрами
Основные определения
Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Рассмотрим уравнение  (1), где
(1), где  — переменные величины. Любая система значений переменных
— переменные величины. Любая система значений переменных  при которой левая и правая части уравнения (1) принимают действительные значения, называется системой допустимых значений
при которой левая и правая части уравнения (1) принимают действительные значения, называется системой допустимых значений  . Пусть
. Пусть  — множество всех допустимых значений переменной
— множество всех допустимых значений переменной  ,
,  — множество допустимых значений
— множество допустимых значений  и т. д.,
и т. д.,  — множество всех допустимых значений
— множество всех допустимых значений  . Если у каждого из множеств
. Если у каждого из множеств 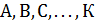 выбрать и зафиксировать по одному значению
выбрать и зафиксировать по одному значению 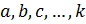 и подставить в уравнение (1), то получим уравнение с одним неизвестным. Переменные
и подставить в уравнение (1), то получим уравнение с одним неизвестным. Переменные  считаются постоянными, называются параметрами, а само уравнение — уравнением с параметрами. Решить уравнение с параметрами — значит указать, при каких значениях параметров существуют решения и каковы они.
считаются постоянными, называются параметрами, а само уравнение — уравнением с параметрами. Решить уравнение с параметрами — значит указать, при каких значениях параметров существуют решения и каковы они.
Основные типы задач
Тип1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.
Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успех и при решении задач всех других основных типов.
Пример 1:Для всех действительных значений параметра с решите уравнение 
Решение. Исходное кубическое по  уравнение является квадратным относительно
уравнение является квадратным относительно  . Поэтому, считая переменную
. Поэтому, считая переменную  параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно
параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно  , опуская промежуточные шаги по раскрытию скобок и перегруппировке:
, опуская промежуточные шаги по раскрытию скобок и перегруппировке:

Поскольку  и
и  , то по обратной теореме Виета
, то по обратной теореме Виета  .
.
Поэтому исходное уравнение равносильно совокупности уравнений
 .
.
Первое уравнение преобразуется к виду  откуда:
откуда:
(1): при  решений нет;
решений нет;
(2): при  единственное решение
единственное решение  при
при  два решения;
два решения;
(3): 
(4): 
Второе уравнение совокупности имеет единственное решение (5):  для любого значения параметра с.
для любого значения параметра с.
Изображаем ось параметра с и отмечаем на ней граничные значения параметра, которые фигурируют в ответах к каждому уравнению совокупности (Рисунок 1).
e CUgXCTB0nVeD6wV8frzcFcBClE5J4x0K+MYA6/r6qpKl8he3xXMbe0YhLpRSgI5xLDkPnUYrw8KP 6Gh38JOVkdqp52qSFwq3hmdJcs+tHBxd0HLEZ43dsT1ZAarZ7Zar49hs9Vd+eDXvqmk3b0Lc3sxP j8AizvEPhl99UoeanPb+5FRgRsCqyFJCBeTpAzACiiynwZ6KZQ68rvj/D+ofAAAA//8DAFBLAQIt ABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhABG23AUlAgAAAgQAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9E b2MueG1sUEsBAi0AFAAGAAgAAAAhAENAThzgAAAACQEAAA8AAAAAAAAAAAAAAAAAfwQAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAACMBQAAAAA= " filled="f" stroked="f">
| с |
(2) 
|
(3) 
|
(4) 
|
(5) 
|
Рисунок 1
Ответ: 
Пример 2:При каком наибольшем отрицательном значении  функцияимеет максимум в точке
функцияимеет максимум в точке  ?
?

Решение. Максимумы функции  достигаются в точках вида
достигаются в точках вида
 Следовательно, чтобы у исходной функции достигался максимум в точке
Следовательно, чтобы у исходной функции достигался максимум в точке  , должно существовать такое число
, должно существовать такое число  , что
, что


Остаётся лишь выбрать среди чисел вида 
наибольшее отрицательное. Это будет число  , получающееся при
, получающееся при  , так как если
, так как если  , то
, то 
Ответ: 
Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).
Пример 1:Сколько корней имеет уравнение  в зависимости от значений параметра
в зависимости от значений параметра 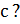
Решение.Область допустимых значений уравнения:  .
.
Запишем уравнение в виде:  . Рассмотрим две функции:
. Рассмотрим две функции:

Построим графики функций (Рисунок 2). График первой функции – это верхняя половина окружности  . График второй функции – биссектрисы первого и второго координатных углов. Из графика первой функции вычтем график второй и получим график функции
. График второй функции – биссектрисы первого и второго координатных углов. Из графика первой функции вычтем график второй и получим график функции  Если заменить
Если заменить  на
на  ,то последний график функции есть множество точек
,то последний график функции есть множество точек  удовлетворяющих исходному уравнению.
удовлетворяющих исходному уравнению.

|

|

|

Рисунок 2
Ответ: при  корней нет;при
корней нет;при  два корня;при
два корня;при  один корень.
один корень.
Пример 2:Сколько корней имеет уравнениев зависимости от параметра  ?
?

Решение. Построим в системе координат  график функции
график функции  , но сначала представим ее в виде:
, но сначала представим ее в виде:


Прямые  являются асимптотами графика функции. График функции
являются асимптотами графика функции. График функции  получается из графика функции
получается из графика функции  смещением на
смещением на  единиц по оси
единиц по оси  (Рисунок 3)
(Рисунок 3)

|

|

|

|

Рисунок 3
Графики функций  и
и  пересекаются в одной точке при
пересекаются в одной точке при  ; значит, исходное уравнение при этих значениях параметра имеет одно решение.
; значит, исходное уравнение при этих значениях параметра имеет одно решение.
При  графики пересекаются в двух точках; значит, при этих значениях параметра исходное уравнение имеет два корня.
графики пересекаются в двух точках; значит, при этих значениях параметра исходное уравнение имеет два корня.
При  графики пересекаются в трех точках; значит, уравнение при этих значениях параметра имеет три решения.
графики пересекаются в трех точках; значит, уравнение при этих значениях параметра имеет три решения.
Замечание:При решении уравнения особо следует обратить внимание на случай, когда  так как точка
так как точка  не принадлежит графику функции
не принадлежит графику функции  но принадлежит графику функции
но принадлежит графику функции 
Ответ:если  то одно решение;
то одно решение;
если  то два решения;
то два решения;
если  то три решения.
то три решения.
Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).
Пример 1:Найти все значения параметра  , при которых система имеет ровно два решения.
, при которых система имеет ровно два решения.

Решение.Преобразуем систему к следующему виду:

Поскольку параметр  находится в основании логарифма, на него накладываются следующие ограничения:
находится в основании логарифма, на него накладываются следующие ограничения:  .Поскольку переменная
.Поскольку переменная  стоит под знаком логарифма, на нее накладывается следующее ограничение:
стоит под знаком логарифма, на нее накладывается следующее ограничение:  .
.
Скомбинировав оба уравнения системы, переходим к уравнению:  . В зависимости от того, какие значения принимает параметр
. В зависимости от того, какие значения принимает параметр  , возможны два случая:
, возможны два случая:
1) Пусть  В этом случае функция
В этом случае функция  убывает в области допустимых значений, а функция
убывает в области допустимых значений, а функция  возрастает в той же области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что корень у уравнения один, при этом он меньше 1. Второе уравнение системы и вся система в целом имеют, следовательно, два решения в силу того, что дискриминант уравнения
возрастает в той же области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что корень у уравнения один, при этом он меньше 1. Второе уравнение системы и вся система в целом имеют, следовательно, два решения в силу того, что дискриминант уравнения  при
при  положителен. Рассматриваемый случай нам полностью подходит.
положителен. Рассматриваемый случай нам полностью подходит.
2) Пусть теперь 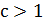 . В этом случае функция
. В этом случае функция  возрастает на области допустимых значений, и функция
возрастает на области допустимых значений, и функция  возрастает в этой области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что пересечься в одной точке они могут только в случае касания друг друга. Однако, касание это может произойти лишь в точке, абсцисса которой больше 1. Второе уравнение системы и вся система в целом, следовательно, иметь решений не будут в силу того, что дискриминант уравнения
возрастает в этой области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что пересечься в одной точке они могут только в случае касания друг друга. Однако, касание это может произойти лишь в точке, абсцисса которой больше 1. Второе уравнение системы и вся система в целом, следовательно, иметь решений не будут в силу того, что дискриминант уравнения  при
при  отрицателен.
отрицателен.
Ответ: 
Пример 2:Найдите все значения  , для каждого из которых уравнение
, для каждого из которых уравнение  имеет единственное решение.
имеет единственное решение.
Сделаем замену  и перенесем все слагаемые в одну часть:
и перенесем все слагаемые в одну часть:

Получили квадратное уравнение, корнями которого по теореме Виета являются  Для того, чтобы исходное уравнение имело один корень, достаточно, чтобы полученное уравнение с
Для того, чтобы исходное уравнение имело один корень, достаточно, чтобы полученное уравнение с  тоже имело один (положительный!) корень. Заметим сразу, что
тоже имело один (положительный!) корень. Заметим сразу, что  при всех
при всех  будет положительным.
будет положительным.
Таким образом, получаем два случая:
1) 


2) Так как  всегда положителен, то
всегда положителен, то  должен быть
должен быть 

Ответ: 
Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Например, найти значения параметра, при которых:
1) уравнение выполняется для любого значения переменной из заданного промежутка;
2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.
Пример 1:При каких значениях параметра  функция определена при всех x
функция определена при всех x  ?
?

Решение. 
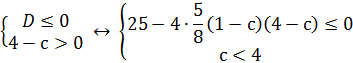


Ответ:с 
Пример 2:Найдите все значения параметра  , при каждом из которых уравнение имеет ровно один корень на отрезке
, при каждом из которых уравнение имеет ровно один корень на отрезке 

Уравнение можно переписать в виде:

Таким образом, заметим, что  является корнем уравнения при любых
является корнем уравнения при любых  , так как уравнение принимает вид
, так как уравнение принимает вид  . Для того, чтобы этот корень принадлежат отрезку
. Для того, чтобы этот корень принадлежат отрезку  нужно, чтобы
нужно, чтобы 
Второй корень уравнения находится из  то есть
то есть  . Для того, чтобы это число было корнем уравнения, нужно, чтобы оно удовлетворяло ОДЗ уравнения, то есть:
. Для того, чтобы это число было корнем уравнения, нужно, чтобы оно удовлетворяло ОДЗ уравнения, то есть:

Для того, чтобы этот корень принадлежал отрезку  нужно, чтобы
нужно, чтобы

Таким образом, чтобы корень  существовал и принадлежал отрезку
существовал и принадлежал отрезку  нужно, чтобы
нужно, чтобы  . Заметим, что тогда при
. Заметим, что тогда при  оба корня
оба корня  и
и  принадлежат отрезку
принадлежат отрезку 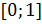 (то есть уравнение имеет два корня на этом отрезке), кроме случая, когда они совпадают:
(то есть уравнение имеет два корня на этом отрезке), кроме случая, когда они совпадают:

Таким образом, нам подходят  и
и 
Ответ: 
Многообразие задач с параметром охватывает весь курс школьной математики (и алгебры, и геометрии), но подавляющая часть из них на выпускных и вступительных экзаменах относится к одному из четырех перечисленных типов, которые по этой причине названы основными.
Наиболее массовый класс задач с параметром — задачи с одной неизвестной и одним параметром.
Основные методы решения задач, содержащих параметр
Аналитический метод
Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.
Пример 1:Найдите все значения параметра  , при которых уравнение:
, при которых уравнение:
 имеет не более одного корня.
имеет не более одного корня.
Решение.При 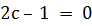 данное уравнение квадратным не является, поэтому случай
данное уравнение квадратным не является, поэтому случай  разберём отдельно.
разберём отдельно.
Если  , то уравнение преобразуется в
, то уравнение преобразуется в  , оно имеет один корень.
, оно имеет один корень.
Если  , то уравнение является квадратным, а чтобы оно имело не более одного корня необходимо, чтобы дискриминант был неположительным.
, то уравнение является квадратным, а чтобы оно имело не более одного корня необходимо, чтобы дискриминант был неположительным.


Чтобы записать окончательный ответ, необходимо понять, удовлетворяет ли  вышеуказанному условию, а для этого надо сравнить числа
вышеуказанному условию, а для этого надо сравнить числа  и
и  ; очевидно, что
; очевидно, что  .
.
Ответ:  U
U  U
U  .
.
Пример 2:Найдите все значения параметра  , при каждом из которых уравнениене имеет решений.
, при каждом из которых уравнениене имеет решений.

Решение.Перепишем уравнение в виде

Найдём множество значений левой части получившегося уравнения. Для этого обозначим  и рассмотрим функцию
и рассмотрим функцию  при
при  . Её производная равна
. Её производная равна  . На отрезке
. На отрезке  производная обращается в ноль при
производная обращается в ноль при  положительна при
положительна при  и отрицательна при
и отрицательна при  . Значит, при
. Значит, при  функция убывает, а при
функция убывает, а при  возрастает. Наименьшее значение функции
возрастает. Наименьшее значение функции  на отрезке – это
на отрезке – это  . Чтобы определить наибольшее значение, найдём значения
. Чтобы определить наибольшее значение, найдём значения  на концах отрезка:
на концах отрезка:  ,
,  Значит, наибольшее значение равно 26, и функция
Значит, наибольшее значение равно 26, и функция  .
.
Следовательно, данное уравнение имеет решения при 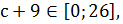 т. е. при
т. е. при  а при всех остальных
а при всех остальных  решений нет.
решений нет.
Ответ: 
Пример 3:Найдите все значения параметра  , при которых уравнениеимеет ровно одно решение.
, при которых уравнениеимеет ровно одно решение.

Данное уравнение равносильно следующему (условие положительности подлогарифмического выражения можно опустить, так как в новом уравнении выходит, что оно равно  при всех
при всех 

Делаем замену  . Получаем уравнение:
. Получаем уравнение:

Исходное уравнение имеет ровно одно решение тогда и только тогда, когда вышеуказанное уравнение имеет ровно одно положительное решение. Это возможно в двух случаях.
1) Вышеуказанное уравнение имеет ровно одно решение и это решение положительно. Это может быть, если  откуда
откуда  Тогда получаем, что
Тогда получаем, что  (один положительный корень)
(один положительный корень)
2) Вышеуказанное уравнениеимеет два корня, один из которых положителен, а другой – нет. В этом случае удобно разобрать два варианта:
А) Одним из корней уравнения является  . Подставляя это значениенаходим, что
. Подставляя это значениенаходим, что  . Тогда уравнение принимает вид
. Тогда уравнение принимает вид 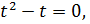 т. е. действительно имеет ровно один положительный корень. Значит
т. е. действительно имеет ровно один положительный корень. Значит  подходит.
подходит.
Б) Один из корней положителен, а второй – отрицателен. Для этого необходимо и достаточно, чтобы выполнялось неравенство  откуда
откуда 
Ответ: 
Пример 4:Найдите все значения параметра  , при каждом из которых система имеет ровно одно решение.
, при каждом из которых система имеет ровно одно решение.

Решение.Заметим, что если пара чисел  является решением этой системы, то пара чисел
является решением этой системы, то пара чисел  также является решением (так как при замене
также является решением (так как при замене  оба уравнения системы не изменяются). Поэтому если решение единственно, то оно имеет вид
оба уравнения системы не изменяются). Поэтому если решение единственно, то оно имеет вид  . Подставляя в систему
. Подставляя в систему  получаем
получаем

откуда находим, что  или
или  . Все остальные значения
. Все остальные значения  нам не подходят (при них система не имеет решений вида
нам не подходят (при них система не имеет решений вида  , поэтому ровно одного решения быть не может).
, поэтому ровно одного решения быть не может).
Проверимподходят ли значения  и
и  . Для этого подставляем найденные
. Для этого подставляем найденные  в исходную систему.
в исходную систему.
1) При  получаем систему
получаем систему

Заметим, что пара чисел  является решением этой системы. Но тогда
является решением этой системы. Но тогда  также является решением. Значит, система имеет более одного решения, поэтому
также является решением. Значит, система имеет более одного решения, поэтому  не подходит.
не подходит.
3) При  получаем
получаем

Из второго уравнения системы следует, что каждая из переменных по модулю не превосходит единицы. Перепишем первое уравнение системы в виде

Заметим, что при  и
и  левая часть уравнения неотрицательна, а правая – не положительна. Действительно,
левая часть уравнения неотрицательна, а правая – не положительна. Действительно,  тогда как
тогда как  кроме того, на промежутке
кроме того, на промежутке  выполняется неравенство
выполняется неравенство  . Значит, равенство может достигаться, только если левая и правая части обращаются в ноль, что возможно при
. Значит, равенство может достигаться, только если левая и правая части обращаются в ноль, что возможно при  Заметим, что эта пара чисел также удовлетворяет второму уравнению системы. Таким образом, при
Заметим, что эта пара чисел также удовлетворяет второму уравнению системы. Таким образом, при  система имеет решение
система имеет решение  и это решение единственно.
и это решение единственно.
Ответ: 
Пример 5:При каких значениях  системаимеет хотя бы одно решение?
системаимеет хотя бы одно решение?

Решение.Если  , то система имеет решения (любая пара чисел, удовлетворяющая условию
, то система имеет решения (любая пара чисел, удовлетворяющая условию  является решением системы, например,
является решением системы, например, 
Если  , то обе части уравнений отличны от нуля, поэтому имеем право разделить первое уравнение на второе. Получаем
, то обе части уравнений отличны от нуля, поэтому имеем право разделить первое уравнение на второе. Получаем  откуда
откуда

Подставляем это во второе уравнение исходной системы и преобразуем:

Для того, чтобы система имела хотя бы одно решение, необходимо и достаточно, чтобы уравнение имело хотя бы одно решение.
При  уравнение не имеет решений, а при всех остальных
уравнение не имеет решений, а при всех остальных  оно равносильно следующему:
оно равносильно следующему:  Множество значений функции в левой части уравнения – это промежуток
Множество значений функции в левой части уравнения – это промежуток 
Поэтому уравнение имеет хотя бы одно решение при
 откуда
откуда 
Ответ: 
Графический метод
|
из
5.00
|
Обсуждение в статье: Основные методы решения задач, содержащих параметр |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

