 |
Главная |
Перестановки. Размещения. Сочетания
|
из
5.00
|
Первый абзац)
2) Отображение
 называется сюръективным (или сюръекцией, или отображением наY), если каждый элемент множестваY является образом хотя бы одного элемента множества X, то есть
называется сюръективным (или сюръекцией, или отображением наY), если каждый элемент множестваY является образом хотя бы одного элемента множества X, то есть 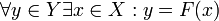
-
 — сюръективно.
— сюръективно. -
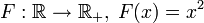 — сюръективно.
— сюръективно. -
 — не является сюръективным (например, не существует такого
— не является сюръективным (например, не существует такого  , что F(x) = − 9).
, что F(x) = − 9).
3)Отображение  называется инъекцией (или вложением), если разные элементы множестваXпереводятся в разные элементы множестваY.
называется инъекцией (или вложением), если разные элементы множестваXпереводятся в разные элементы множестваY.
-
 — инъективно.
— инъективно. -
 — инъективно.
— инъективно. -
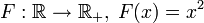 — не является инъективным (F( - 2) = F(2) = 4).
— не является инъективным (F( - 2) = F(2) = 4).
4) Функция 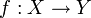 называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она:
- Переводит разные элементы множестваX в разные элементы множества Y (инъективность). Иными словами,
-
 .
. - Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами,
-
 .
.
Биекцию также называют взаимно однозначным отображением (взаимно однозначным соответствием [1]). Множества, для которых существует биекция, называются равномощными.
Биекция множества на себя является перестановкой элементов этого множества.
Примеры
-
 — функция, сохраняющая все элементы множества X, биективна на этом множестве.
— функция, сохраняющая все элементы множества X, биективна на этом множестве. -
 — биективные функции из
— биективные функции из  в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией.
в себя. Вообще, любой моном одной переменнойнечетнойстепени является биекцией. - f(x) = ex — биективная функция в
 . Но если её рассматривать как функцию в
. Но если её рассматривать как функцию в  , то она уже не будет биективной (у нуля и отрицательных чисел не будет прообразов).
, то она уже не будет биективной (у нуля и отрицательных чисел не будет прообразов). - f(x) = sinx не является биективной функцией, если считать её определённой на всём
 .
.
5)Отношение эквивалентности (  ) на множествеX — это бинарное отношение, для которого выполнены следующие условия:
) на множествеX — это бинарное отношение, для которого выполнены следующие условия:
- Рефлексивность:
 для любого a в X,
для любого a в X, - Симметричность: если
 , то
, то  ,
, - Транзитивность: если
 и
и  , то
, то  .
.
6)Классом эквивалентностиC(a) элемента a называется подмножество элементов, эквивалентных a. Из вышеприведённого определения немедленно следует, что, если 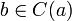 , то C(a) = C(b).
, то C(a) = C(b).
Бинарное отношениеR на множествеX называется отношением порядка, или отношением частичного порядка, если имеют место
- Рефлексивность:

- Транзитивность:
 ;
; - Антисимметричность:
 .
.
Множество X, на котором введено отношение частичного порядка, называется частично упорядоченным.
Примеры отношений порядка
- На множестве вещественных чисел отношения «больше» и «меньше» являются отношениями строгого порядка, а «больше или равно» и «меньше или равно» — нестрогого.
- Отношение делимости на множестве целых чисел являются отношением нестрогого порядка.
Второй абзац)
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Перестановки. Размещения. Сочетания
Пусть есть некоторое конечное множество элементов U={a1, a2, ..., an}. Рассмотрим набор элементов  ,
,  где ÎU, j = 1, 2, ..., r.
где ÎU, j = 1, 2, ..., r.
Этот набор называется выборкой объема r из n элементов. Любое подмножество U является выборкой, но не всякая выборка является подмножеством U, так как в выборку один и тот же элемент может входить несколько раз (в отличие от подмножества).
Принцип суммы: если cardA = m, cardB = n и AÇB = Æ , то cardAÈB = =m+n. На комбинаторном языке это означает: если объект A можно выбрать m способами, объект B другими n способами и их одновременный выбор невозможен, то выбор “A или B” может быть осуществлен m+n способами.
Принцип произведения: если cardA=m, cardB=n, то card (A´B)=m*n. На комбинаторном языке это означает: если объект A может быть выбран m способами, при любом выборе A объект B может быть выбран n способами, то выбор “A и B” может быть осуществлен m*n способами.
Пример 1. A = 10 {различных шоколадок}, B = 5 { различных пачек печенья}. Выбор “A или B” означает, что выбирается что-то одно и способов выбора в этом случае будет 15. Выбор “A и B” означает, что выбирается 1 шоколадка и 1 пачка печенья и различных вариантов для такого выбора будет 50.
Рассмотрим основные способы формирования выборок.
Определение. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Если порядок следования элементов несущественен, то выборка называется неупорядоченной.
Из определения следует, что две упорядоченные выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, являются различными.
Перестановки. Упорядоченные выборки, объемом n из n элементов, где все элементы различны, называются перестановками из n элементов. Число перестановок из n элементов обозначается Pn.
Теорема.P = n!
Доказательство проводится по индукции. Очевидно, если n = 1, то перестановка только одна и P1 = 1!. Пусть для n = k теорема верна и Pk= k!, покажем, что она тогда верна и для n = k+1. Рассмотрим (k+1)- й элемент, будем считать его объектом A, который можно выбрать k+1 способами. Тогда объект B – упорядоченная выборка из оставшихся k элементов по k. B соответствии с индуктивным предположением объект B можно выбрать k! способами. По принципу произведения выбор A и B можно осуществить k!(k+1) = (k+1)! способами. Совместный выбор A и B есть упорядоченная выборка из k + 1 элементов по k + 1.
Пример 3. Сколько существует способов, чтобы расположить на полке 10 различных книг? Ответ: 10!
Размещения. Упорядоченные выборки объемом m из n элементов (m<n), где все элементы различны, называются размещениями. Число размещений из n элементов по m обозначается  .
.
Теорема.  =
= 
Обозначим x =  . Тогда оставшиеся (n – m) элементов можно упорядочить (n – m)! способами. По принципу произведения, если объект A можно выбрать x способами, объект B (n – m)! способами, то совместный выбор “A и B” можно осуществить x×(n – m)! способами, а выбор “A и B” есть перестановки и Pn = n! Отсюда x =
. Тогда оставшиеся (n – m) элементов можно упорядочить (n – m)! способами. По принципу произведения, если объект A можно выбрать x способами, объект B (n – m)! способами, то совместный выбор “A и B” можно осуществить x×(n – m)! способами, а выбор “A и B” есть перестановки и Pn = n! Отсюда x =  =
= 
Рассуждая иначе: первый элемент выбираем n способами, второй – (n – 1) способами и т.д. , m–й элемент выбираем (n – m + 1) способом. По принципу произведения вновь имеем: n(n – 1)...(n – m +1), что совпадает с  .
.
Пример 4. Группа из 15 человек выиграла 3 различных книги. Сколькими способами можно распределить эти книги среди группы?
Имеем  = 15 ×14 ×13 = 2730.
= 15 ×14 ×13 = 2730.
Сочетания. Неупорядоченные выборки объемом m из n элементов (m<n) называются сочетаниями. Их число обозначается  .
.
Теорема. 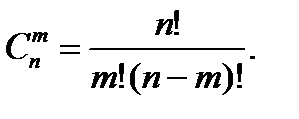
Доказательство. Очевидно,  Действительно, объект A – неупорядоченная выборка из n элементов по m, их число
Действительно, объект A – неупорядоченная выборка из n элементов по m, их число  . После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “A и B“ – упорядоченная выборка.
. После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “A и B“ – упорядоченная выборка.
Пример 5. Группа из 15 человек выиграла 3 одинаковых книги. Сколькими способами можно распределить эти книги?
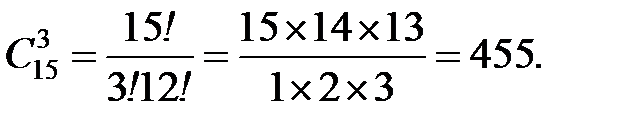
Сочетания, размещения и перестановки являлись подмножествами исходного множества. Рассмотрим выборки, которые не являются подмножествами.
Размещения с повторениями. Упорядоченные выборки объемом m из n элементов, где элементы могут повторяться, называются размещениями с повторениями. Их число обозначается  (n).
(n).
Теорема.  (n) = nm.
(n) = nm.
Доказательство. Первый элемент может быть выбран n способами, второй элемент также может быть выбран n способами и так далее, m -й элемент также может быть выбран n способами. По принципу произведения получаем nm .
Пример 6. Кодовый замок состоит из четырех разрядов, в каждом разряде независимо от других могут быть выбраны цифры от 0 до 9. Сколько возможных комбинаций?
Здесь n = 10, m = 4 и ответом будет 104.
Пример 7. Рассмотрим вектор длины m, каждая координата которого может принимать всего 2 значения: 0 или 1. Сколько будет таких векторов?
Это есть выборка, объемом m из двух элементов.Ответ:2m
Перестановки с повторениями. Пусть имеется n элементов, среди которых k1 элементов первого типа, k2 элементов второго типа и т.д., ksэлементов s-го типа, причем k1 + k2 + ... + ks = n. Упорядоченные выборки из таких n элементов по n называются перестановками с повторениями, их число обозначается Cn(k1, k2, ..., ks). Числа Cn(k1, k2, ..., ks) называются полиномиальными коэффициентами.
Теорема. Cn(k1, ..., ks)= 
Доказательство проведем по индукции по s, т. е. по числу типов элементов. При s = 1 утверждение становится тривиальным: k1 = n, все элементы одного типа и Cn(n) = 1. В качестве базы индукции возьмем s = 2, n = k1 +k2. В этом случаем перестановки с повторениями превращаются в сочетания из n элементов по k1 (или k2): выбираем k1 место, куда помещаем элементы первого типа.
Cn(k1,k2) = 
Пусть формула верна для s = m , т.е. n = k1 + ... + km и
Cn(k1, ..., km)= 
Докажем, что она верна для s = m + 1 (n = k1 +... + km + km+1). В этом случае перестановку с повторениями можно рассматривать как совместный выбор двух объектов: объект A – выбор k m + 1 места для элементов (m + 1)-го типа; объект B – перестановка с повторениями из (n – km+1) элементов. Объект A можно выбрать  способом, B –
способом, B –  (k1, ..., km) способами. По принципу произведения
(k1, ..., km) способами. По принципу произведения


и мы получили требуемую формулу.
Замечание. Числа  называются биноминальными коэффициентами. Из этой формулы следует, что
называются биноминальными коэффициентами. Из этой формулы следует, что 
Пример 8. Сколько различных слов можно получить, переставляя буквы в слове “математика”?
Решение. Буква “а” входит 3 раза (k1= 3), буква “м” – 2 раза (k2 = 2), “т” – 2 раза (k3 = 2), буквы “е”, ”к”, ”и” входят по одному разу, отсюда k3 = k4 = k5 = 1.
C10 (3, 2, , 2, 1, 1, 1) =  =151200.
=151200.
Сочетания с повторениями. Пусть имеется n типов элементов, каждый тип содержит не менее m одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³m´n ) называется сочетанием с повторением. Число сочетаний с повторениями обозначается  (n).
(n).
Теорема.  (n) =
(n) =  .
.
Доказательство. Пусть в выборку вошло m1 элементов первого типа, m2 элементов второго типа, ...mn – n-го типа. Причем каждое 0 £m i£m и m1+m2+ ...+ mn= =m. Сопоставим этой выборке вектор следующего вида:  Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов {bn} существует биекция (докажите это!). Следовательно,
Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов {bn} существует биекция (докажите это!). Следовательно,  (n) равно числу векторов bn. “ Длина вектора” bn равна числу 0 и 1, или m+ +n–1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n- 1 мест, а это будет
(n) равно числу векторов bn. “ Длина вектора” bn равна числу 0 и 1, или m+ +n–1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n- 1 мест, а это будет  .
.
Задачи.
1. Существует ли функция вида (где коэффициенты a0, a1, ..., an; b0, b1, ..., bn - целые числа), обладающая следующим свойством: для любого рационального числа r найдется такое целое число k, что f(k)=r.
2. Найти биекцию числовой прямой на интервал (а, в).
3. Найти биекцию полуотрезка [0, 1) на полуось [0, ¥).
4. Построить биекцию отрезка [0, 1] на всю числовую ось.
5. Существует ли непрерывная функция, являющаяся биекцией отрезка [а, в] на всю числовую ось?
6. Существует ли непрерывная функция, являющаяся биекцией отрезка [а, в] на интервал (с, d)?
7. Установить биекцию между открытым и замкнутым единичным кругом.
8. Какова мощность множества всех треугольников на плоскости, вершины которых имеют рациональные координаты?
9. Какова мощность множества всех рациональных функций с целыми коэффициентами в числителе и знаменателе?
10. Доказать, что множество точек разрыва монотонной функции, определенной на всей числовой прямой, не более чем счетно.
11. Пусть Е - счетное множество точек на прямой. Можно ли так сдвинуть это множество на величину а (т.е. заменить все точки хÎЕ точками х + а), чтобы получившееся в результате сдвига множество Еa не пересекалось с Е?
12. Пусть Е — счетное множество точек на окружности. Можно ли повернуть окружность вокруг центра на некоторый угол j так, чтобы множество Еj, получившееся из Е в результате поворота, не пересекалось с Е?
13. Доказать, что если расстояние между любыми двумя точками множества Е на прямой больше единицы, то множество Е не более чем счетно.
14. Какова мощность множества всех строго возрастающих последовательностей натуральных чисел?
15. Какова мощность множества всех последовательностей натуральных чисел, не содержащих число 7?
16. Какова мощность множества всех многочленов (с произвольными вещественными коэффициентами)?
17. Какова мощность множества всех отрезков на числовой прямой?
18. На числовой прямой задано множество попарно непересекающихся отрезков. Какова его мощность?
19. Какова мощность множества всех строго возрастающих непрерывных функций на отрезке [а, в]?
20. Доказать, что если А — В равномощно В — А, то А и В равномощны.
21. Доказать, что если А Í В и А равномощно АÈС, то В равномощно ВÈС.
22. Верно или нет утверждение: “Если А равномощно С, В равномощно D, причем А Ê В, С Ê D, то А — В равномощно С — D”?
23. Доказать, что множество всех конечных подмножеств счетного множества — счетно.
24. Какова мощность множества всех конечных и счетных подмножеств множества Е, если Е имеет мощность континуума?
Вариантов же много, можно точно так же тангенсом:  .
.
maxmatem в сообщении #245899 писал(а):
Не совсем понимаю по какому принципу составляются биекции след рода:
1. 
4. 
Когда у меня возникает нужда в поиске такого отбражения (а случается это примерно раз в два года), я пользую функцию  . Для реализации
. Для реализации  пишу:
пишу:  ; приходится выбрать
; приходится выбрать  . Т.е.
. Т.е.  . Далее замечаю, что
. Далее замечаю, что  , и спокойно можно принять
, и спокойно можно принять  (обоснование понятно?). Чтобы сделать
(обоснование понятно?). Чтобы сделать  , обнуляю знаменатель:
, обнуляю знаменатель:  , т.е.
, т.е.  ,
, 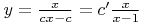 (
(  ). Далее убеждаюсь, что получл строго монотонную на (0,1) функцию, без всяких выпендрёжек типа разрывов внутри этого интервала. Наконец, выбираю какое-нибудь конкретное
). Далее убеждаюсь, что получл строго монотонную на (0,1) функцию, без всяких выпендрёжек типа разрывов внутри этого интервала. Наконец, выбираю какое-нибудь конкретное  , например,
, например,  , если хочется повыпендриваться, или
, если хочется повыпендриваться, или  , если хочется выглядеть человеком обыкновенным.
, если хочется выглядеть человеком обыкновенным.
|
из
5.00
|
Обсуждение в статье: Перестановки. Размещения. Сочетания |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

