Однородная система линейных уравнений

Рассмотрим линейную систему:

,                                                                         

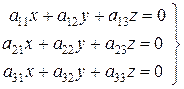свободные члены которой равны нулю. Такая система называется однородной.

Однородная система всегда обладает нулевым (тривиальным) решением : , то есть она всегда совместна. Если определитель системы , то нулевое решение единственное.

Если , но один из миноров второго порядка определителя системы отличен от нуля, тогда одно из уравнений есть следствие двух других, и данная система сводится к системе двух уравнений с двумя неизвестными, имеющей бесчисленное множество ненулевых решений.

Если  и все миноры второго порядка равны нулю, то система сводится к одному уравнению с тремя неизвестными, следовательно, данная система также имеет бесчисленное множество решений.

 

Пример. Решить однородную систему:

 

Определитель системы , следовательно, система имеет единственное решение

 

Пример. Решить однородную систему:

 

Определитель системы , следовательно, система имеет бесконечное множество ненулевых решений. Заметим, что миноры, содержащиеся в первых двух строках определителя, отличны от нуля, например

Для получения третьего уравнения надо прибавить к первому уравнению второе, то есть третье уравнение - следствие первых двух, следовательно, система сводится к двум уравнения:

Считая произвольной одну переменную, например, z=h, получим:

Решая эту систему уравнений методом Крамера, найдём x и y

Главный определитель этой системы 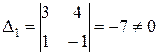, побочные определители , . Тогда

 

Пример 3. . Решить однородную систему:

 

Определитель системы  и все миноры второго порядка равны нулю, имеем одно независимое уравнение (второе и третье уравнения получаются из первого умножением его, соответственно, на 2 или 3). Полагая произвольными две переменные, например, , , имеем

§ 4 Исследование системы m линейных уравнений с n неизвестными.

Дана система m – линейных уравнений с n – неизвестными:

                                                           (1)

Определение: Матрица А= - матрица системы (1), а матрица  - расширенная матрица системы (1)

 

Теорема Кронекара-Капелли: Для совместности системы (1) необходимо и достаточно, чтобы ранг матрицы А был равен рангу расширенной матрицы :

r(A)=r( )=r.

В этом случае число r называется рангом системы (1).

Определение: Если 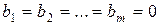, то система линейных уравнений (1) называется однородной. Однородная система уравнений всегда совместна. Если ранг совместной системы равен числу неизвестных (r=n), то система является определённой. Если же ранг совместной системы меньше числа неизвестных (r<n), то система неопределенна.

Пусть система (1) совместна, причём r<n . Рассмотрим какой-нибудь базисный минор матрицы А. Выделим в этом миноре произвольную строку. Элементами этой строки являются коэффициентами при r неизвестных в одном из уравнений системы (1). Эти r неизвестных назовём базисными неизвестными рассматриваемой системы уравнений. Остальные n - r неизвестных системы (1) назовём свободными неизвестными .

Выделим из системы (1) систему r-уравнений, среди коэффициентов которых содержатся элементы базисного минора. Базисные неизвестные в выделенной системе оставим в левых частях уравнений, а члены содержащие свободные неизвестные, перенесём вправо. Из полученной системы уравнений выразим базисные неизвестные через свободные неизвестные (например, по формулам Крамера).

Таким образом, придавая свободным неизвестным произвольные значения, можно найти соответствующие значения базисных неизвестных, следовательно, система имеет бесчисленное множество решений.

 

 

Пример. Исследовать систему уравнений:

Матрица системы , расширенная матрица системы . Определим ранги этих матриц.

 

~ ~ ~

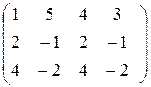~ , Отсюда r(A)=2, так как

 

~  ~ ~

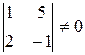
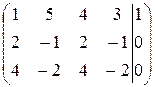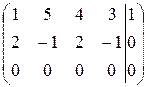Получаем, что r(A )=2, следовательно, r(A)=r( )=r, следовательно, система совместна. По условию количество неизвестных n=4, а ранг системы r=2, то есть r<n, значит, система неопределенна.

Возьмём первое и второе уравнение исходной системы:

 

За базисные неизвестные примем . Это можно сделать, так как определитель 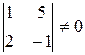. Свободными неизвестными служат 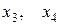. Имеем

Пусть , где 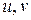 - любые числа

Решаем эту систему методом Крамера:

системы уравнений.

 

ГЛАВА III ЛИНЕЙНЫЕ ПРОСТРАНСТВА. ЛИНЕЙНЫЕ
ПРЕОБРАЗОВАНИЯ

Линейные пространства

П.1 Основные понятия

Рассмотрим такое множество R элементов …., в котором для любых двух элементов  определена сумма  и  и для любого действительного числа  определено произведение .

Определение: Если сложение элементов множества R и умножение элемента этого множества на действительное число удовлетворяющее следующим условиям:

1)

2)

3)  такой нуль-элемент , что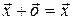

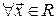
4) Для любого элемента  существует  такой, что , в дальнейшем будем писать , то есть

5)

7) ( ) ;

8) ,

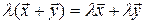то множество называется линейным (или векторным) пространством, а элементы этого пространства – векторами.

Например, множество всех геометрических векторов является линейным пространством, так как для элементов этого множества определены действия сложения и умножения на число, удовлетворяющие сформулированным условиям.

Определение: Разностью двух векторов  и  линейного пространства называется такой вектор  этого пространства, что . Разность векторов  и  обозначается - , то есть - = , причём - = +(- ).

 

Справедливы следующие теоремы:

1. В каждом линейном пространстве  только один нуль-элемент;

2. Элемент (-1)  является противоположным для элемента

3. Для любого элемента линейного пространства 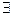 только один противоположный элемент;

4. Для любого элемента  выполняется равенство 0 ;

5. Для любого действительно числа  и нуль-элемента  выполняется равенство ;

6. Из равенства  следует одно из двух равенств:  или .