 |
Главная |
Идеи методов одномерной оптимизации
|
из
5.00
|
Численные методы оптимизации классифицируются следующим образом.
1. По размерности решаемых задач: одномерные; многомерные.
Одномерная оптимизация: Метод сканирования. Метод деления пополам. Метод золотого сечения. Метод параболической аппроксимации.
Многомерная безусловная градиентная оптимизация: Метод градиента. Метод наискорейшего спуска. Метод сопряженных градиентов. Метод тяжелого шарика.
Многомерная безградиентная оптимизация: Метод Гаусса-Зайделя (покоординатный спуск). Метод Розенброка. Симплексный метод (метод дифференцируемого многогранника). Метод параллельных касательных.
Многомерная случайная оптимизация: Метод слепого поиска. Метод случайного направления. Метод поиска с «наказанной случайностью». Метод с «блуждающим» поиском.
Многомерная условная оптимизация: Метод штрафов. Метод прямого поиска с возвратом. Метод проектирования градиента.
Постановка: требуется оптимизировать х (формальная постановка)

 - функция одной переменной
- функция одной переменной 
 - целевая функция.
- целевая функция.
Решение: найти х, при котором  принимает оптимальное значение.
принимает оптимальное значение.
2 варианта:
- минимизировать – задача минимизации;
- максимизировать – задача максимизации.
Рассмотрим случай минимизации


2 способа:
- аналитический
- численный
В аналитическом  задается в виде формулы, в численном
задается в виде формулы, в численном  задается в виде черного ящика, на входе подается х, на выходе значение целевой функции в этой точке.
задается в виде черного ящика, на входе подается х, на выходе значение целевой функции в этой точке.
Пусть функция определена в некоторой области S (  ), в случае одномерной оптимизации S – интервал
), в случае одномерной оптимизации S – интервал  :
:
1. точка  называется глобальным минимумом, если для
называется глобальным минимумом, если для 
2. точка  называется строгим глобальным минимумом, если для
называется строгим глобальным минимумом, если для 
3. точка  называется локальным минимумом, если для
называется локальным минимумом, если для 
4. точка  называется строгим локальным минимумом, если для
называется строгим локальным минимумом, если для 
Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.
Аналитический способ нахождения локального минимума.
 - дифференцируема
- дифференцируема
 - необходимое условие точки локального минимума.
- необходимое условие точки локального минимума.
 | |||
 | |||
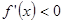

 |



Численные методы
 Пусть функция
Пусть функция  задана на интервале
задана на интервале  , при этом существует такая точка
, при этом существует такая точка  , что на
, что на  – монотонно убывает, а на
– монотонно убывает, а на  – монотонно возрастает, то функция унимодальная.
– монотонно возрастает, то функция унимодальная.
 |
а  b
b
Если из того что  следует, что
следует, что  , то функция называется монотонно возрастающей. Если из того что
, то функция называется монотонно возрастающей. Если из того что  следует, что
следует, что 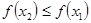 , то функция называется монотонно убывающей.
, то функция называется монотонно убывающей.
Методы одномерного поиска
Разобьем  и вычислим значение функции в каждой точке.
и вычислим значение функции в каждой точке.
 |




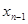

искомый минимум
В результате остается интервал меньшего размера, к которому применяется тот же метод, и находим еще один интервал, в конце находим интервал с заведомо нужной точкой.
Интервал неопределенности – интервал, в котором заведомо находится точка минимума. Наиболее эффективное разбиение – двумя точками на 3 равных отрезка.
 |




1) 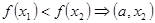
2) 
 - после выполнения n шагов сокращение исходного интервала
- после выполнения n шагов сокращение исходного интервала

 - точность с которой надо найти решение задачи.
- точность с которой надо найти решение задачи.


N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).
Метод золотого сечения
Точки должны быть расположены на равном расстоянии.










 а b
а b
 |


 ;
;  ;
;  ;
;
 ;
;  - золотое сечение.
- золотое сечение.

 а
а
 |


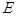

 - величина сокращения на каждом шаге
- величина сокращения на каждом шаге

число итераций растет как логарифм функции.
Одномерная оптимизация с использованием производных
 . Пусть целевая функция дифференцируема
. Пусть целевая функция дифференцируема  .
.
| 
|   
| |||
| точка локального минимума | точка локального максимума | точка перегиба |
Методы для нахождения корня уравнения функции 1-ой производной от исходной
Нахождение локального минимума или максимума сводится к нахождению корней первой производной от данной
f ’( x )=0
Если f’(x) представляет собой многочлен, то уравнение называется алгебраическим (полиномиальным), если f’(x) представлена тригонометрическими, логарифмическими, показательными и т.п. функциями, то уравнение называется трансцендентным.( вдальнйшем вместо f ’( x ) будем употреблять f ( x ) )
Решение уравнения вида  разбивается на два этапа:
разбивается на два этапа:
1. отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;
2. вычисление выделенного корня с заданной точностью.
На первом этапе может помочь построение приближенного графика функции f(x) или, если функция достаточно сложная, то можно попытаться представить уравнение в виде  и построить два графика
и построить два графика 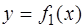 и
и  , тогда корнями уравнения будут абсциссы точек пересечения этих кривых.
, тогда корнями уравнения будут абсциссы точек пересечения этих кривых.
Выбор интервалов, в которых имеется один и только один корень производится на основании известных свойств непрерывных функций:
- Если на концах некоторого интервала  функция
функция  непрерывна и принимает значения разных знаков, т.е.
непрерывна и принимает значения разных знаков, т.е.  , то на этом интервале уравнение
, то на этом интервале уравнение  имеет хотя бы один корень (один или нечетное количество корней).
имеет хотя бы один корень (один или нечетное количество корней).
- Если на концах интервала  функция
функция  принимает значения одинаковых знаков, т.е.
принимает значения одинаковых знаков, т.е.  , то на этом интервале уравнение
, то на этом интервале уравнение  не имеет корней или имеет четное количество корней.
не имеет корней или имеет четное количество корней.
- Если на интервале  первая и вторая производные функции сохраняют определенный знак, т.е.
первая и вторая производные функции сохраняют определенный знак, т.е.  и
и  или
или  и
и  , и не обращаются в нуль на всем участке, то функция монотонна, и корень будет единственным.
, и не обращаются в нуль на всем участке, то функция монотонна, и корень будет единственным.
Для вычисления выделенного корня существует множество приближенных методов. Все они вычисляют значение корня уравнения с заданной степенью точности  , т.е. заданное количество цифр после запятой. Рассмотрим следующие методы:
, т.е. заданное количество цифр после запятой. Рассмотрим следующие методы:
- половинного деления;
Метод половинного деления
Суть метода половинного деления (дихотомии) заключается в следующем.
Отрезок  делится пополам и за первое приближение корня принимается точка c, которая является серединой отрезка, т.е.
делится пополам и за первое приближение корня принимается точка c, которая является серединой отрезка, т.е.  . Если
. Если  , это корень уравнения. Если нет, то далее выбирается тот из отрезков [a, c] или [c, b], на концах которого функция имеет разные знаки. Полученный отрезок снова делится пополам, и проводятся те же рассуждения. Деление продолжается до тех пор, пока длина отрезка не станет меньше заданного
, это корень уравнения. Если нет, то далее выбирается тот из отрезков [a, c] или [c, b], на концах которого функция имеет разные знаки. Полученный отрезок снова делится пополам, и проводятся те же рассуждения. Деление продолжается до тех пор, пока длина отрезка не станет меньше заданного  .
.
Метод половинного деления реализуется в виде следующего алгоритма:
Найти точку c = (a + b)/2.
Если f(a)×f(c) <0, то корень лежит на интервале [a, c], если нет, то корень лежит на интервале [c, b].
Если величина интервала не превышает некоторое достаточно малое число е, то найден корень с точностью е, иначе возврат к п.1.
Несмотря на простоту, этот метод требует слишком большого количества вычислений и не всегда позволяет найти решение с заданной точностью. 


Блок-схема алгоритм решения уравнения методом деления пополам.
Список использованной литературы
1. Автоматизация вычислений и компьютерное моделирование. MS Excel и MathCad : учебное пособие / Н.В. Вознесенская. – Саранск : Изд-во Мордовского университета, 2004. – 91 с.
2. Дьяконов, В. MathCad 2001: специальный справочник / В. Дьяконов. – СПб. : Питер, 2002. – 832 с.
3. Информатика : учебник / Макарова Н. В. [и др.]. – М. : Финансы и статистика, 1997. —768с.
4. Исследование операций в экономике: Учебное пособие для вузов / Кремер Н.Ш. [и др.]. – М.: ЮНИТИ, 2002. – 407 с.
5.Кудрявцев, Е. Н. Исследования операций в задачах, алгоритмах и программах / Е.Н. Кудрявцев. М., Наука, 1982. – 150 с.
6.Кузнецов, Ю. Н. Математическое программирование / Ю.Н. Кузнецов, В.И. Кузубов, А.В. Волощеноко. - М.: Высшая школа, 1980. – 320 с.
7. Леонтьев, Ю. Microsoft Office 2000. Краткий курс / Ю. Леонтьев. – СПб.: Питер, 2001. – 760 с.
8.Сидоров, М. Е. Решение задач оптимального планирования в таблицах Excel // Информатика и образование. – М., 2001. – № 1. – с. 36 – 51.
9.Стандарт предприятия. Общие требования и правила оформления курсовых и дипломных работ и пояснительных записок к курсовым и дипломным проектам.
10. Ширяев, В.Д. Экономико-математические методы: учебное пособие / В.Д. Ширяев, Н.М. Куляшова. – Саранск : Изд-во Мордовского университета, 2002. – 112 с.
11. Экономическая информатика: Учебник / Косарев В.П.. – М.: Финансы и статистика, 2004. – 592 с.
|
из
5.00
|
Обсуждение в статье: Идеи методов одномерной оптимизации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


